Задачи на движение протяженных тел
Протяженными будем считать тела, длина которых соизмерима с расстоянием, которое они проезжают.
В задачах на движение протяженных тел обычно требуется определить длину одного из них. Наиболее типичные ситуации, предлагаемые в таких задачах, - определить длину поезда проезжающего мимо:
придорожного столба;
идущего параллельно путям пешехода;
лесополосы определенной длины;
другого двигающегося поезда.
Помним, что во всех задачах на движение используется только одна формула: это формула пути 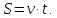
Если поезд движется мимо столба, то он проходит расстояние равное его длине. Обозначим:
l – длина поезда,
v – скорость поезда,
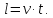
Если поезд движется мимо протяженной лесополосы (платформы), то он проходит расстояние равное сумме длины самого поезда и лесополосы. Обозначим:
l1 – длина поезда,
l2 – длина лесополосы (платформы),
v – скорость поезда,
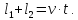
Если поезд движется мимо движущегося человека, то учитываем направление движения человека. Если он движется навстречу, то скорости складываются, если в одну сторону, то находим разность скоростей. Обозначим:
l – длина поезда,
v1 – скорость поезда,
v2 – скорость человека,
В одну сторону: 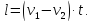
В разные стороны: 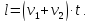
Если поезд движется мимо движущегося поезда, то учитываем направление движения второго поезда. Если он движется навстречу, то скорости складываются, если в одну сторону, то находим разность скоростей. Обозначим:
l1 – длина первого поезда,
l2 – длина второго поезда,
v1 – скорость первого поезда,
v2 – скорость второго поезда,
В одну сторону: 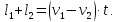
В разные стороны: 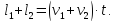
Рассмотрим несколько задач.
Задача 1. Поезд, двигаясь равномерно со скоростью 60км/ч, проезжает мимо придорожного столба за 30 секунд. Найти длину поезда в метрах.
Решение:
v = 60 км/ч = 1000 м/мин, t = 30 сек. = 1/2 мин. Длину поезда находим как пройденное расстояние: 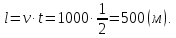
Ответ: 500 метров.
Задача 2. Поезд, двигаясь равномерно со скоростью 90 км/ч, проезжает мимо лесополосы, длина которой равна 800 метрам, за 1 минуту. Найти длину поезда в метрах.
Решение:
v = 90 км/ч = 1500 м/мин, t = 1 мин. Тогда пройденное поездом расстояние: 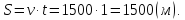
Это собственная длина поезда плюс длина лесополосы. Длина поезда равна: 1500 – 800 = 700 (м).
Ответ: 700 метров.
Задача 3. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и товарный поезда, скорости которых равны соответственно 90 км/ч и 30 км/ч. Длина товарного поезда равна 600 метрам. Найдите длину пассажирского поезда, если время, за которое он прошёл мимо товарного поезда, равно 1 минуте. Ответ дайте в метрах.
Решение: Так как поезда двигаются в одном направлении, их относительная скорость равна:
v = 90 – 30 = 60 км/ч = 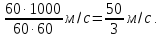
За 60 секунд один поезд проходит мимо другого, то есть преодолевает расстояние:
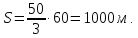
Это длина пассажирского и товарного поездов. Тогда длина пассажирского поезда равна:
1000 – 600 = 400 (м).
Ответ: 400 метров.
Задача 4. По двум параллельным железнодорожным путям навстречу друг другу следуют скорый и пассажирский поезда, скорости которых равны соответственно 65 км/ч и 35 км/ч. Длина пассажирского поезда равна 700 метрам. Найдите длину скорого поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 36 секундам. Ответ дайте в метрах.
Решение: Так как поезда двигаются в противоположных направлениях, их относительная скорость равна:
v = 65 + 35 = 100 км/ч = 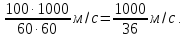
За 36 секунд один поезд проходит мимо другого, то есть преодолевает расстояние:
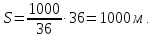
Это расстояние, равное сумме длин обоих поездов. Значит, длина скорого поезда равна:
1000 – 700 = 300 (м).
Ответ: 300 метров.
Задача 5. Поезд проходит мимо неподвижного наблюдателя за 7 секунд, а мимо платформы длиной 378 метров – за 25 секунд. Найдите длину поезда.
Решение: Из первого условия следует, что за 7 секунд поезд проедет расстояние, равное собственной длине поезда. За 25 же секунд ему надо проехать собственно саму длину платформы, т.е. 378 метров и ещё надо «вытащить» головной вагон вперед на расстояние, равное длине поезда.
1) 25 – 7 = 18 (с) – время, за которое поезд проехал 378 м
2) 378 : 18 = 21 (м/с) – скорость поезда
3) 21 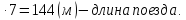
Ответ: 144 м.
Задача 6. По двум параллельным железнодорожным путям в одном направлении следуют пассажирский и скорый поезда. Скорый поезд, двигаясь со скоростью 120 км/ч, догнал пассажирский поезд и прошёл мимо него за 100 секунд. Найдите скорость пассажирского поезда, если его длина составляет 800 метров, а длина скорого поезда – 700 метров. Ответ дайте в км/ч.
Решение: Считаем, что пассажирский поезд неподвижен, а скорый приближается к нему со скоростью, равной разности скоростей поездов.
1) 700 + 800 = 1500 (м) – прошёл скорый поезд за 100 секунд
2) 1500 : 100 = 15 (м/с) – разность скоростей (скорость вдогонку)
15 м/с =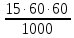 км/ч = 54 км/ч
км/ч = 54 км/ч
3) 120 – 54 = 66 (км/ч) – скорость пассажирского поезда.
Ответ: 66 км/ч.
Задача 7. По морю параллельными курсами в одном направлении следуют два сухогруза: первый длиной 110 метров, второй — длиной 90 метров. Сначала второй сухогруз отстает от первого, и в некоторый момент времени расстояние от кормы первого сухогруза до носа второго составляет 1000 метров. Через 16 минут после этого уже первый сухогруз отстает от второго так, что расстояние от кормы второго сухогруза до носа первого равно 400 метрам. На сколько километров в час скорость первого сухогруза меньше скорости второго?
Решение: Пока сухогрузы перейдут из первого положения во второе, второй сухогруз переместился относительно первого на
1000 + 110 + 90 + 400 = 1600 (м).
Пусть v — разность скоростей сухогрузов, тогда
v = 1600 : 16 = 100 м/мин = 6 км/ч.
Ответ: на 6 км/ч.







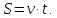
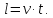
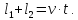
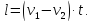
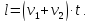
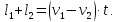
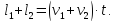
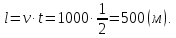
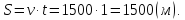
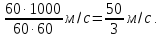
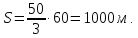
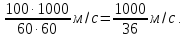
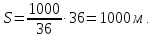
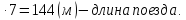
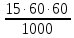 км/ч = 54 км/ч
км/ч = 54 км/ч









