Специально к окончанию учебного года! Скидки до 50% на комплекты видеоуроков и электронных тетрадей

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до 23.05.2025

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 15.05.2025 07:29

Домаш Надежда Анатольевна

Учитель математики

60 лет

209

156 066

Подписчики

Подписки

Местоположение

Россия, Жуковский

Специализация

Математика

Алгебра

Геометрия

Обо мне Блог Файлы Тесты Галерея Активность Награды

Задачи на уроках итогового повторения по теме "Площади фигур" в 9 классе при подготовке к ОГЭ

Категория: Геометрия

02.10.2023 21:36

Данная разработка содержит задания для итогового повторения курса геометрии в 9 классе.

Просмотр содержимого документа
«Задачи на уроках итогового повторения по теме "Площади фигур" в 9 классе при подготовке к ОГЭ»

Первая часть.

1. В равнобедренном треугольнике боковая сторона равна 10, основание  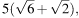— , а угол, лежащий напротив основания, равен150°.Найдите площадь треугольника.

2. Два катета прямоугольного треугольника равны 14 и 5. Найдите площадь этого треугольника.

3. Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 19. Найдите площадь этого треугольника.

4. Высота BH ромба ABCD делит его сторону AD на отрезки AH=24 и HD=2. Найдите площадь ромба.

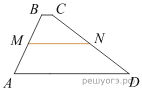
5. В трапеции ABCD известно, что AD =  9, BC  =  1, а её площадь равна 20. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.

6. Найдите площадь прямоугольника, если его периметр равен 58 и одна сторона на 5 больше другой.

7. Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, а угол сектора равен 120°. В ответе укажите площадь, деленную на π.

8. Найдите площадь квадрата, если его диагональ равна 3.

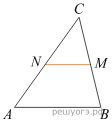
9. В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 45. Найдите площадь четырёхугольника ABMN.

10. Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а синус угла между ней и одним из оснований равен 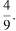. Найдите площадь трапеции.

11. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH = 8 и HD =  40. Диагональ параллелограмма BD равна 50. Найдите площадь параллелограмма.

12. Площадь прямоугольного треугольника равна 450 корень из 3 . Один из острых углов равен 60°. Найдите длину катета, прилежащего к этому углу.

13. Найдите площадь квадрата, описанного вокруг окружности радиуса 7.

14. В прямоугольнике одна сторона равна 10, периметр равен 44. Найдите площадь прямоугольника.

15. Радиус круга равен 3, а длина ограничивающей его окружности равна 6π. Найдите площадь круга. В ответ запишите площадь, деленную на π.

16. Высота равностороннего треугольника равна 10. Найдите его площадь, делённую на дробь: числитель: корень из 3 , знаменатель: 3 конец дроби .

17. Периметр ромба равен 28, а один из углов равен 30°. Найдите площадь ромба.

18. Радиус круга равен 1. Найдите его площадь, деленную на π.

19. Найдите площадь прямоугольника, если его периметр равен 102, а отношение соседних сторон равно 2:15.

Вторая часть.

Задача 1. Два равных прямоугольника имеют общую вершину O (см. рис.). Докажите, что площади треугольников AOK и COM равны.

Задача 2. Докажите, что медиана треугольника делит его на два треугольника, площади которых равны между собой.

Задача 3. Докажите, что отрезок, соединяющий середины оснований трапеции, делит её на две равные по площади части.

Задача 4. В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.

Задача 5. Точка E — середина боковой стороны AB трапеции ABCD. Докажите, что площадь треугольника ECD равна половине площади трапеции.

Задача 6. Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.

Задача 7. В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке O. Докажите, что площади треугольников AOB и COD равны.