Задачи на вероятность

Тема урока

Решение задач по теории вероятностей

.

МОУ «Осташевская средняя общеобразовательная школа

Качайкина Н.Б.

С.И.Ожегов, Н.Ю.Шведова

« Вероятность – возможность исполнения, осуществимости чего-нибудь».

А.Н.Колмогоров

« Вероятность математическая – это числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях ».

Классическое определение вероятности

«Вероятностью Р(А) события А в испытании с равновозможными элементарными исходами называется отношение числа исходов т, благоприятствующих событию А, к числу п всех исходов испытания».

Р(А) = т/п

Математическая модель «игральная кость»

Испытание – бросание игральной кости

Событие – выпадение очков

Выпадение каждой грани при многократном бросании кубика

имеет одинаковую вероятность

Устная работа

1. Игральную кость (кубик) бросили один раз.

Какова вероятность того, что выпало 4 очка?

2. Игральную кость (кубик) бросили один раз.

Какова вероятность того, что выпало не более 4

очков?

3. Игральную кость (кубик) бросили один раз.

Какова вероятность того, что выпало менее 4

очков?

4. Игральную кость (кубик) бросили один раз.

Какова вероятность того, что выпало нечетное

число очков?

Решите задачу

1. В случайном эксперименте бросают две игральные

кости. Найдите вероятность того, что сумма

выпавших очков равна 6. Ответ округлите

до сотых .

2. В случайном эксперименте бросают две игральные

кости. Найдите вероятность того, что в сумме

выпадет 3 очка. Результат округлите

до сотых.

3. В случайном эксперименте бросают две игральные

кости. Найдите вероятность того, что в сумме

выпадет более 10 очков. Результат округлите

до сотых

Решите задачу

• Люда дважды бросает игральный кубик. В сумме у неё выпало 9 очков. Найдите вероятность того, что при одном из бросков выпало 5 очков.

• Саша дважды бросает игральный кубик. В сумме у него выпало 6 очков. Найдите вероятность того, что при одном из бросков выпало

1 очко.

• Аня дважды бросает игральный кубик. В сумме

у нее выпало 5 очков. Найдите вероятность того, что при первом броске выпало 3 очка.

Решите задачу

7. Наташа и Вика играют в кости. Они бросают

игральную кость по одному разу. Выигрывает тот,

кто выбросил больше очков. Если очков выпало

поровну, то наступает ничья. В сумме выпало 8

очков. Найдите вероятность того, что Наташа

выиграла.

8. Тоня и Нина играют в кости. Они бросают

игральную кость по одному разу. Выигрывает тот,

кто выбросил больше очков. Если очков выпало

поровну, то наступает ничья. В сумме выпало 6

очков. Найдите вероятность того, что Тоня

проиграла

Решите задачу

9. Коля и Лёша играют в кости. Они бросают

игральную кость по одному разу. Выигрывает тот,

кто выбросил больше очков. Если очков выпало

поровну, то наступает ничья. Первым бросил

Коля, у него выпало 3 очка. Найдите

вероятность того, что Лёша не выиграет.

10. Миша трижды бросает игральный кубик. Какова

вероятность того, что все три раза выпадут

чётные числа?

11. В случайном эксперименте бросают три

игральные кости. Найдите вероятность того, что в

сумме выпадет 16 очков. Результат округлите

до сотых.

Решение задачи № 1

Результат каждого бросания – это пара чисел ( a , b ), где a и b – числа от 1 до 6. Поэтому все поле событий состоит из 6х6 = 36 элементов ( п = 36 )

Благоприятным исходом для рассматриваемого события является любая пара ( a , b ), для которой a + b = 6.

1

1

2

2

2

3

3

3

3

4

4

4

4

4

5

5

5

5

5

5

6

6

6

6

6

6

6

7

7

7

7

7

7

8

8

8

8

8

9

9

9

9

10

10

10

11

11

12

Это можно сделать пятью следующими способами:

6 = 1 + 5

6 = 2 + 4

6 = 3 + 3

6= 4 + 2

6 = 5 + 1

( т = 5 )

Таким образом, вероятность заданного события равна

Р = т/п =5/36 = 0,14

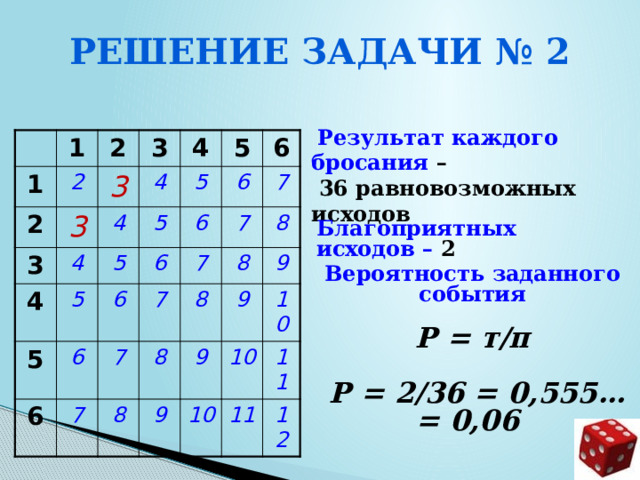
Решение задачи № 2

Результат каждого бросания –

36 равновозможных исходов

1

1

2

2

2

3

3

3

3

4

4

4

4

4

5

5

5

5

5

5

6

6

6

6

6

6

6

7

7

7

7

7

7

8

8

8

8

8

9

9

9

9

10

10

10

11

11

12

Благоприятных исходов – 2

Вероятность заданного события

Р = т/п

Р = 2/36 = 0,555… = 0,06

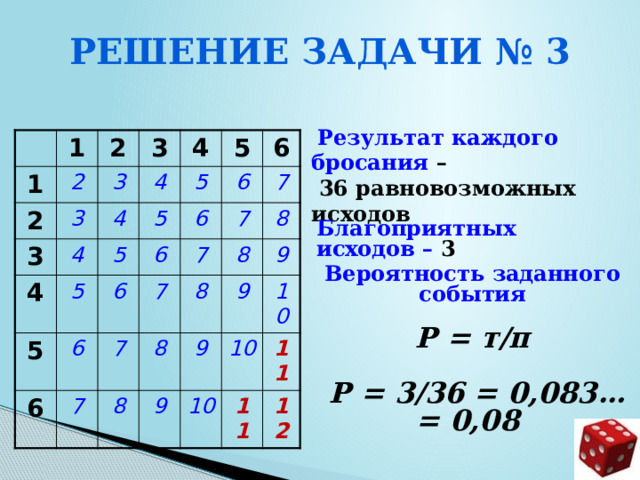
Решение задачи № 3

Результат каждого бросания –

36 равновозможных исходов

1

1

2

2

2

3

3

3

3

4

4

4

4

4

5

5

5

5

5

5

6

6

6

6

6

6

6

7

7

7

7

7

7

8

8

8

8

8

9

9

9

9

10

10

10

11

11

12

Благоприятных исходов – 3

Вероятность заданного события

Р = т/п

Р = 3/36 = 0,083… = 0,08

Решение задачи № 4

Первое бросание Второе бросание Сумма очков

3 + 6 = 9

4 + 5 = 9

5 + 4 = 9

6 + 3 = 9

Равновозможных исходов – 4

Благоприятствующих исходов – 2

Вероятность события р = 2/4 = 0,5

Решение задачи № 5

Первое бросание Второе бросание Сумма очков

1 + 5 = 6

2 + 4 = 6

3 + 3 = 6

4 + 2 = 6

5 + 1 = 6

Равновозможных исходов – 5

Благоприятствующих исходов – 2

Вероятность события р = 2/5 = 0,4

Решение задачи № 6

Первое бросание Второе бросание Сумма очков

1 + 4 = 5

2 + 3 = 5

3 + 2 = 5

4 + 1 = 5

Равновозможных исходов – 4

Благоприятствующих исходов – 1

Вероятность события р = 1/4 = 0,25

Решение задачи № 7

Наташа Вика Сумма очков

2 + 6 = 8

3 + 5 = 8

4 + 4 = 8

5 + 3 = 8

6 + 2 = 8

Равновозможных исходов – 5

Благоприятствующих исходов – 2

Вероятность события р = 2/5 = 0,4

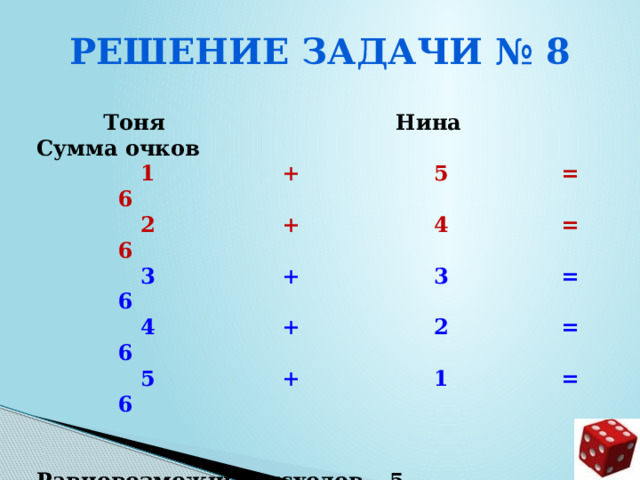
Решение задачи № 8

Тоня Нина Сумма очков

1 + 5 = 6

2 + 4 = 6

3 + 3 = 6

4 + 2 = 6

5 + 1 = 6

Равновозможных исходов – 5

Благоприятствующих исходов – 2

Вероятность события р = 2/5 = 0,4

Решение задачи № 9

У Коли выпало 3 очка.

У Лёши равновозможных исходов – 6

Благоприятствующих проигрышу исходов – 3

(при1 и при 2 и при 3)

Вероятность события р = 3/6 = 0,5

Решение задачи № 10

У Миши равновозможных исходов – 6 · 6 · 6 = 216

Благоприятствующих проигрышу исходов – 3 · 3 · 3 = 27

Вероятность события р = 27/216 = 1/8 = 0,125

Решение задачи № 11

Первая Вторая Третья Сумма очков

4 + 6 + 6 = 16

6 + 4 + 6 = 16

6 + 6 + 4 = 16

5 + 5 + 6 = 16

5 + 6 + 5 = 16

6 + 5 + 5 = 16

Равновозможных исходов – 6 · 6 · 6 = 216

Благоприятствующих исходов – 6

Вероятность события р = 6/216 = 1/36 = 0,277… = 0,28

Домашняя работа

• В случайном эксперименте бросают три игральные кости. В сумме выпало 12 очков. Найдите вероятность того, что при первом броске выпало 3 очка. Результат округлите до сотых.

• Даша трижды бросает игральный кубик. Какова вероятность того, что все три раза выпадут одинаковые числа?