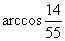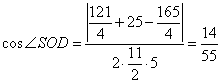Задание 13 Вариант 12 ЕГЭ 2022 Ященко

Задание 13 Вариант 13 ЕГЭ 2022 Ященко

Задание 13. В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами АВ = 8 и ВС = 6. Длины боковых рёбер пирамиды SA= √21, SB = √85, SD = √57.

а) Докажите, что SA — высота пирамиды.

б) Найдите угол между прямыми SC и BD.

Решение.

а)Рассмотрим треугольник SAB, в котором по условию задания: SA= √21, AB = 8, SB = √57.Можно заметить, что

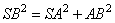
и согласно обратной теореме Пифагора треугольникSAB – прямоугольный, с гипотенузой SB и катетами SA и AB.

Рассмотрим треугольник SAD со сторонами: SD = √57, SA= √21, AD = 6 (так как в основании пирамиды лежит четырехугольник, поэтому AD = BC). Здесь также:

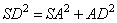
и по обратной теореме Пифагора имеем прямоугольный треугольник SAD с гипотенузой SD и катетами SA и AD.

Так как 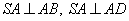 , то по признаку перпендикулярности прямой и плоскости  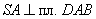 и SA–высота пирамиды.

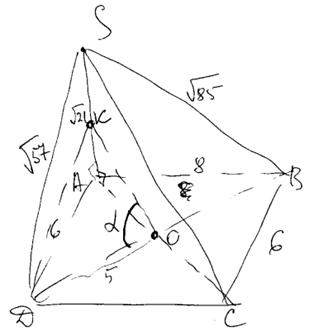
б)Так как ABCD – прямоугольник, то точка O лежит на пересечении его диагоналей и делит их пополам, то есть, O–середина отрезка BD. Сделаем построение – отрезок KO как средняя линия треугольника SAC, причем, 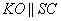 . Тогда угол между SC и BDбудет также равен углу KOD.

Найдем косинус угла SOD из треугольника KOD. В соответствии с теоремой косинусов, имеем:

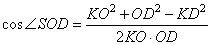
Рассмотрим прямоугольный треугольник SDC (прямоугольный, так как 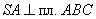  и 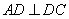  - по теореме о трех перпендикулярах получаем, что  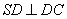). По теореме Пифагора:

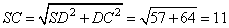
Тогда KO = SC:2 = 11:2. Далее, диагональ

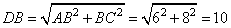
Следовательно, DO = DB:2 = 5. Точка K – середина SA, имеем: 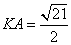 и

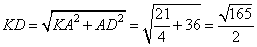
Получаем косинус угла:

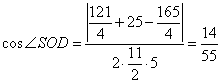
и

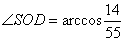
Ответ: