Задание 16. Вариант 8. ЕГЭ 2020 из 36 вариантов.
Четырёхугольник ABCD вписан в окружность радиуса R = 27. Известно, что АВ = ВС = CD = 36.
а) Докажите, что прямые ВС и AD параллельны.
б) Найдите AD.
Решение.
а) Острые углы ВСА и CAD равны, поскольку опираются на равные хорды АВ и CD. Значит, прямые ВС и AD параллельны.
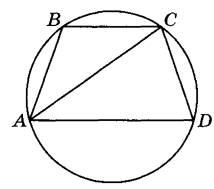
б) Обозначим угол ВСА через α. По теореме синусов

Треугольник ABC равнобедренный, поэтому  . Значит,
. Значит, 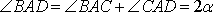 .
.
Четырёхугольник ABCD — равнобедренная трапеция, поэтому 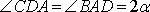 . Значит,
. Значит,
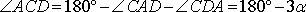
Таким образом, по теореме синусов для треугольников ACD и АСВ получаем:
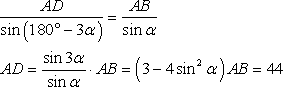
Ответ: 44.
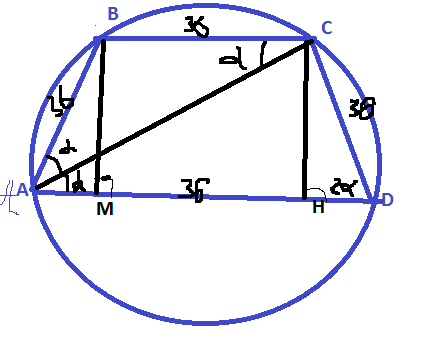 Второй способ решения части б). Проведем 2 высоты: ВМ и СН. Треугольник АВМ прямоугольный. Угол А равен 2α. Тогда АМ= АВcos2α=36cos2α=36(1-2sin²α)=36(1-2·4/9)=36·1/9=4; HD=4 ,AD=2·4+36=44.
Второй способ решения части б). Проведем 2 высоты: ВМ и СН. Треугольник АВМ прямоугольный. Угол А равен 2α. Тогда АМ= АВcos2α=36cos2α=36(1-2sin²α)=36(1-2·4/9)=36·1/9=4; HD=4 ,AD=2·4+36=44.
Ответ: 44.
Задания для самостоятельного решения.
Задание 16. Четырёхугольник ABCD вписан в окружность радиуса R = 12. Известно, что АВ = ВС = CD = 18.
а) Докажите, что прямые ВС и AD параллельны.
б) Найдите AD.
Ответ: 13,5.
Задание 16. Четырёхугольник ABCD вписан в окружность радиуса R = 8. Известно, что АВ = ВС = CD = 12.
а) Докажите, что прямые ВС и AD параллельны.
б) Найдите AD.
Ответ: 9
Задание 16. Четырёхугольник ABCD вписан в окружность радиуса R = 10. Известно, что АВ = ВС = CD = 6.
а) Докажите, что прямые ВС и AD параллельны.
б) Найдите AD.
Ответ: 15,84








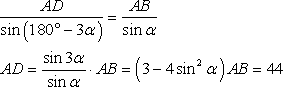
 Второй способ решения части б). Проведем 2 высоты: ВМ и СН. Треугольник АВМ прямоугольный. Угол А равен 2α. Тогда АМ= АВcos2α=36cos2α=36(1-2sin²α)=36(1-2·4/9)=36·1/9=4; HD=4 ,AD=2·4+36=44.
Второй способ решения части б). Проведем 2 высоты: ВМ и СН. Треугольник АВМ прямоугольный. Угол А равен 2α. Тогда АМ= АВcos2α=36cos2α=36(1-2sin²α)=36(1-2·4/9)=36·1/9=4; HD=4 ,AD=2·4+36=44.



















