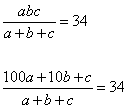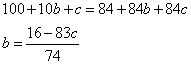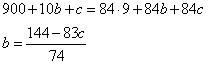Россия, Энгельс
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 07.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 10.02.2025 11:49
Затеева Валентина Павловна
учитель математики
70 лет
790 582
12 
Местоположение
Специализация
Задание 18. Вариант 5 из 36 вариантов Ященко
Категория:
Математика
20.12.2021 06:48
Просмотр содержимого документа
«Задание 18. Вариант 5 из 36 вариантов Ященко»
Задание 18. Вариант 5 из 36 вариантов Ященко
Отношение трёхзначного натурального числа к сумме его цифр – целое число.
а) Может ли это отношение быть равным 34?
б) Может ли это отношение быть равным 84?
в) Какое наименьшее значение может принимать это отношение, если первая цифра трёхзначного числа равна 4?
Решение.
Любое натуральное трехзначное число abc можно записать в виде:
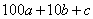
а) Запишем отношение трехзначного числа к сумме его цифр:
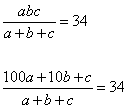
откуда
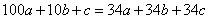
Подберем цифры a, b, c чтобы выполнялось это равенство. Например, при a = 2, имеем:
Здесь только один вариант: b = 0; c = 2. Получаем трехзначное число 102, которое при делении на сумму цифр дает 34.
б) Рассуждаем аналогично. Из равенства
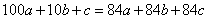
при a = 1, имеем:
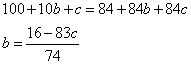
Какое бы значение c мы ни взяли, не получим целого значения для b.
Проверим при a = 9 (второй крайний случай):
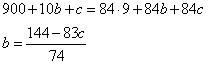
Здесь также нет ни одного значения c, которое бы приводило к целым значениям b.
в) Первая цифра натурального трехзначного числа a = 4. Получаем выражение для отношения:
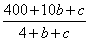
Отсюда видно, чтобы это выражение было минимальным, цифра b должна быть как можно меньше, а c – как можно больше. Будем действовать полным перебором, начиная с b = 9 и c = 0. Получаем наименьшее значение 26 при цифрах: a = 4, b = 6, c = 8.
Ответ: а) да; б) нет; в) 26
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
