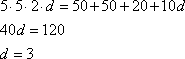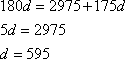Задание 19. Вариант 29 ЕГЭ 2020 из 36 вариантов

Задание 19. Вариант 29 ЕГЭ 2020 из 36 вариантов

Задание 19. а) Приведите пример четырёхзначного числа, произведение цифр которого в 10 раз больше суммы цифр этого числа.

б) Существует ли такое четырёхзначное число, произведение цифр которого в 175 раз больше суммы цифр этого числа?

в) Найдите все четырёхзначные числа, произведение цифр которых в 50 раз больше суммы цифр этого числа.

Решение.

а) Пусть a,b,c,d – цифры четырехзначного числа. Их произведение должно быть в 10 раз больше  их суммы, т.е.

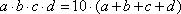
или в виде

.

Возьмем числа a и b кратные 10, например, 5, а число c, также кратное 10, равное 2, получим уравнение для d:

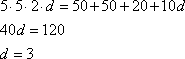
Значение d соответствует цифре 3, значит, мы удачно выбрали предыдущие цифры a, b и c. Таким образом, получили число

5523.

Путем подбора можно найти и другие четырехкратные числа, удовлетворяющие этому условию.

Ответ: 5523.

б) Поступаем аналогично, имеем уравнение

.

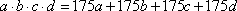Рассуждаем аналогично. Чтобы получить d как цифру, она должна быть в диапазоне от 1 до 9 (цифра 0 исключается, т.к. в произведении даст 0). Для этого, множитель перед d должен получиться больше 175. Подберем первые три цифры так, чтобы получилось ближайшее большее к 175: a=5, b=6, c=6

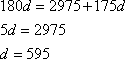
Не соответствует цифре. Найдем наибольшее число для d: a=9, b=9, c=9:

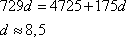
не является целым значением. Попробуем найти его при: a=9, b=9, c=8:

Также не является целым и больше 9, следовательно, другие варианты будут приводить к 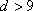 , что не является цифрой. Следовательно, нельзя подобрать четырехзначное число, удовлетворяющее данному условию.

Ответ: нет.

в) Для уравнения

возьмем цифры a=5, b=5, c=8, получим для d:

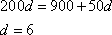
Получили четырехзначное число

5586.

Можно заметить, что все остальные четырехзначные числа будут соответствовать всем возможным перестановкам найденных цифр, то есть получаем варианты:

5568, 5658, 6558, 6585, 6855, 8655, 8565, 8556, 5856, 5865, 5685,

то есть всего 12 вариантов.

Ответ: 5586 и еще 11 вариантов.