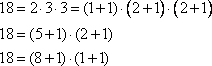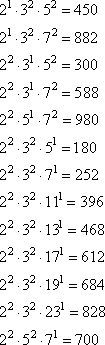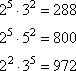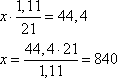Россия, Энгельс
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 07.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 10.02.2025 11:49
Затеева Валентина Павловна
учитель математики
70 лет
790 582
12 
Местоположение
Специализация
Задание 19. Вариант 33. ЕГЭ 2020 из 36 вариантов
Категория:
Математика
11.06.2020 14:42
Просмотр содержимого документа
«Задание 19. Вариант 33. ЕГЭ 2020 из 36 вариантов»
Задание 19. Вариант 33. ЕГЭ 2020 из 36 вариантов
Задание 19. а) Приведите пример трёхзначного числа, у которого ровно 7 натуральных делителей.
б) Существует ли такое трёхзначное число, у которого ровно 21 натуральный делитель?
в) Сколько существует таких трёхзначных чисел, у которых ровно 18 натуральных делителей?
Решение.
а) Рассмотрим трехзначное число, например, 121, оно разлагается на два простых числа 11 и 11:
.
Если к степеням простых множителей добавить 1 и полученные числа перемножить, то получим общее число делителей числа. В данном случае имеем
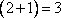
- общее число делителей числа 121, это числа: 1, 11 и 121.
Чтобы получить ровно 7 делителей можно взять число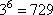 
, у которого будет 6+1=7 делителей. Это делители: 1, 3, 9, 27, 81, 243, 729.
Ответ: 729.
б) Если у числа 21 делитель, то можно, например, подобрать простые множители со степенью 20, но минимальное число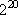 
- это явно не трехзначное число. Вместе с тем, число 21 можно представить в виде произведения 
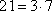и взять множители 
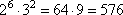. У числа 576
21 делитель:
1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 32, 36, 48, 64, 72, 96, 144, 192, 288, 576.
Ответ: 576.
в) Ровно 18 делителей для трехзначных чисел можно получить следующим образом. Число 18 можно представить в виде множителей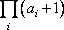 
следующими вариантами:
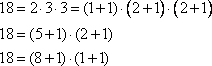
То есть для получения трехзначных чисел с 18-ю делителями, необходимо перебрать все простые множители, с соответствующим числом делителей и степенями:
- для первого варианта имеем:
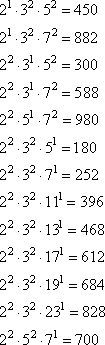
- для второго варианта:
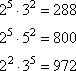
- для третьего варианта:
.
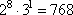Всего имеем 17 вариантов трехзначных чисел с 18-ю делителями.
Ответ: 17.
Задание 17. 15 января планируется взять кредит в банке на 21 месяц. Условия его возврата таковы:
- 1-го числа каждого месяца долг возрастает на 1 % по сравнению с концом предыдущего месяца;
- со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
- 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.
Известно, что на 11-й месяц кредитования нужно выплатить 44,4 тыс. рублей. Какую сумму нужно вернуть банку в течение всего срока кредитования?
Решение.
Пусть 
тыс. рублей сумма взятого кредита в банке. В первый месяц сумма долга увеличивается на 1%, что составит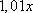 
тыс. рублей. Долг выплачивается в течение 21 месяца так, чтобы долг на одну и ту же величину был меньше долга на 15-е число предыдущего месяца. То есть, после первого месяца нужно выплатить 
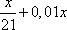тыс. рублей. Оставшаяся сумма долга будет равна
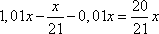тыс. рублей.
После второго месяца сумма долга будет равна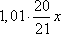 
, а выплата составит 
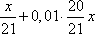. Сумма долга будет равна
.
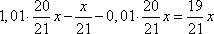Таким образом, на 11-й месяц нужно выплатить
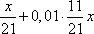
или в виде
По условию задачи выплата на 11-й месяц кредитования составила 44,4 тыс. рублей. Получаем уравнение
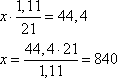
Имеем кредит, равный 840 тыс. рублей. Тогда общая сумма выплат в течение 21 месяца составит
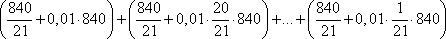
или в виде
То есть 932,4 тыс. рублей или 932400 рублей.
Ответ: 932400.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
