Задания 14 (C2). Углы и расстояния в пространстве

Задания 14 (C2). Углы и расстояния в пространстве

4. Расстояние от точки до пря­мой и до плоскости

1. За­да­ние 14 № 484570. В кубе 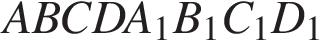все ребра равны Най­ди­те рас­сто­я­ние от точки 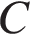до пря­мой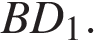

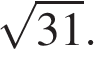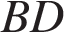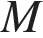2. За­да­ние 14 № 484573. Дана пра­виль­ная тре­уголь­ная пи­ра­ми­да с вер­ши­ной Бо­ко­вое ребро пи­ра­ми­ды равно вы­со­та равна Най­ди­те рас­сто­я­ние от се­ре­ди­ны бо­ко­во­го ребра до пря­мой где точки и 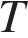— се­ре­ди­ны ребер 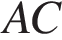и со­от­вет­ствен­но.

3. За­да­ние 14 № 512357. Все рёбра пра­виль­ной тре­уголь­ной пи­ра­ми­ды SBCD с вер­ши­ной S равны 9.

Ос­но­ва­ние O вы­со­ты SO этой пи­ра­ми­ды яв­ля­ет­ся се­ре­ди­ной от­рез­ка SS₁, M — се­ре­ди­на ребра SB , точка L лежит на ребре CD так, что CL : LD = 7 : 2.

а) До­ка­жи­те, что се­че­ние пи­ра­ми­ды SBCD плос­ко­стью S₁LM — рав­но­бо­кая тра­пе­ция.

б) Вы­чис­ли­те длину сред­ней линии этой тра­пе­ции.

4. За­да­ние 14 № 507651. В кубе ABCDA₁B₁C₁D₁ все реб­ра равны 1. Най­ди­те рас­сто­я­ние от точки C до пря­мой AD₁

5. За­да­ние 14 № 507458. Ос­но­ва­ни­ем пря­мой приз­мы ABCDA₁B₁C₁D₁ яв­ля­ет­ся ромб ABCD, у ко­то­ро­го AB = 10, BD = 12. Вы­со­та приз­мы равна 6. Най­ди­те рас­сто­я­ние от цен­тра грани A₁B₁C₁D₁ до плос­ко­сти BDC₁.

6. За­да­ние 14 № 507690. Ос­но­ва­ни­ем пря­мой приз­мы ABCA₁B₁C₁ яв­ля­ет­ся рав­но­бед­рен­ный тре­уголь­ник ABC, AB = AC = 5, BC = 6. Вы­со­та приз­мы равна 3. Най­ди­те рас­сто­я­ние от се­ре­ди­ны ребра B₁C₁ до плос­ко­сти BCA₁.

7. За­да­ние 14 № 507490. Дан куб ABCDA₁B₁C₁D₁ с реб­ром . Най­ди­те рас­сто­я­ние от се­ре­ди­ны ребра B₁C₁ до пря­мой МТ, где точки М и Т — се­ре­ди­ны ребер AD и A₁B₁ со­от­вет­ствен­но.

8. За­да­ние 14 № 507666. Дан куб ABCDA₁B₁C₁D₁ с реб­ром 1. Най­ди­те рас­сто­я­ние от вер­ши­ны A до плос­ко­сти A₁BT, где T — се­ре­ди­на ребра AD.

9. За­да­ние 14 № 507645. Длина ребра куба ABCDA₁B₁C₁D₁ равна 1. Най­ди­те рас­сто­я­ние от вер­ши­ны B до плос­ко­сти ACD₁.

10. За­да­ние 14 № 507502. В ос­но­ва­нии пря­мой тре­уголь­ной приз­мы ABCA₁B₁C₁ лежит рав­но­бед­рен­ный пря­мо­уголь­ный тре­уголь­ник ABC с ги­по­те­ну­зой AB, рав­ной 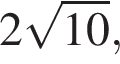вы­со­та приз­мы равна Най­ди­те рас­сто­я­ние от точки C₁ до плос­ко­сти BCM, где M — се­ре­ди­на ребра A₁C₁.

11. За­да­ние 14 № 507669. Дан пра­виль­ный тет­ра­эдр MABC с реб­ром 1. Най­ди­те рас­сто­я­ние между пря­мы­ми AL и MO, где L — се­ре­ди­на ребра MC, O — центр грани ABC.

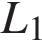12. За­да­ние 14 № 507681. Ребро ос­но­ва­ния пра­виль­ной тре­уголь­ной приз­мы LMNL₁M₁N₁ равно её вы­со­те и равно Най­ди­те рас­сто­я­ние от точки до плос­ко­сти 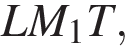где 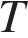— се­ре­ди­на ребра L₁N₁.

13. За­да­ние 14 № 500007. Ос­но­ва­ни­ем пря­мой приз­мы 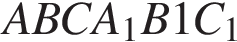яв­ля­ет­ся рав­но­бед­рен­ный тре­уголь­ник бо­ко­вая сто­ро­на ко­то­ро­го равна а угол равен Най­ди­те рас­сто­я­ние от точки до пря­мой если из­вест­но, что бо­ко­вое ребро дан­ной приз­мы равно 12.

14. За­да­ние 14 № 507763. В пра­виль­ной ше­сти­уголь­ной пи­ра­ми­де SABCDEF, сто­ро­ны ос­но­ва­ния ко­то­рой равны 1, а бо­ко­вые рёбра равны 2, най­ди­те рас­сто­я­ние от точки C до пря­мой SA.

15. За­да­ние 14 № 507766. В пра­виль­ной ше­сти­уголь­ной пи­ра­ми­де SABCDEF, сто­ро­ны ос­но­ва­ния ко­то­рой равны 1, а бо­ко­вые рёбра равны 2, най­ди­те рас­сто­я­ние от точки C до пря­мой SF.

16. За­да­ние 14 № 507769. В тет­ра­эд­ре ABCD, все рёбра ко­то­ро­го равны 1, най­ди­те рас­сто­я­ние от точки A до пря­мой, про­хо­дя­щей через точку B и се­ре­ди­ну E ребра CD.

17. За­да­ние 14 № 507775. В пра­виль­ной четырёхуголь­ной пи­ра­ми­де SABCD, сто­ро­на ос­но­ва­ния равна 1, а бо­ко­вое ребро равно Най­ди­те рас­сто­я­ние от точки C до пря­мой SA.

18. За­да­ние 14 № 507778. В пра­виль­ной тре­уголь­ной приз­ме ABCA₁B₁C₁ вы­со­та равна 2, сто­ро­на ос­но­ва­ния равна 1. Най­ди­те рас­сто­я­ние от точки B₁ до пря­мой AC₁.

19. За­да­ние 14 № 507785. В пра­виль­ной тре­уголь­ной приз­ме ABCA₁B₁C₁ вы­со­та равна 1, а ребро ос­но­ва­ния равно 2. Най­ди­те рас­сто­я­ние от точки A₁ до пря­мой BC₁.

20. За­да­ние 14 № 507794. В ос­но­ва­нии пря­мой приз­мы ABCA₁B₁C₁ лежит пря­мо­уголь­ный тре­уголь­ник ABC, у ко­то­ро­го угол C равен 90°, угол A равен 30°, Диа­го­наль бо­ко­вой грани B₁C со­став­ля­ет угол 30° с плос­ко­стью AA₁B₁. Най­ди­те вы­со­ту приз­мы.

21. За­да­ние 14 № 507800. Ос­но­ва­ни­ем пря­мой приз­мы MNKM₁N₁K₁ яв­ля­ет­ся пря­мо­уголь­ный тре­уголь­ник MNK, у ко­то­ро­го угол N равен 90°, угол M равен 60°, NK = 18. Диа­го­наль бо­ко­вой грани M₁N со­став­ля­ют угол 30° с плос­ко­стью MM₁K₁. Най­ди­те вы­со­ту приз­мы.

22. За­да­ние 14 № 507816. В пра­виль­ной ше­сти­уголь­ной приз­ме ABCDEFA₁B₁C₁D₁E₁F₁ все рёбра ко­то­рой равны 1, най­ди­те ко­си­нус угла между пря­мы­ми AB₁ и BC₁.

23. За­да­ние 14 № 507822. В пра­виль­ной ше­сти­уголь­ной приз­ме ABCDEFA₁B₁C₁D₁E₁F₁ все рёбра ко­то­рой рав­ный 1, най­ди­те ко­си­нус угла между пря­мы­ми AB₁ и BD₁.

24. За­да­ние 14 № 511106. В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC с вер­ши­ной S? все рёбра ко­то­рой равны 4, точка N — се­ре­ди­на ребра AC, точка O центр ос­но­ва­ния пи­ра­ми­ды, точка P делит от­ре­зок SO в от­но­ше­нии 3:1, счи­тая от вер­ши­ны пи­ра­ми­ды.

а) До­ка­жи­те, что пря­мая NP пер­пен­ди­ку­ляр­на пря­мой BS.

б) Най­ди­те рас­сто­я­ние от точки B до пря­мой NP.

25. За­да­ние 14 № 484571. Дан куб Длина ребра куба равна Най­ди­те рас­сто­я­ние от се­ре­ди­ны от­рез­ка до плос­ко­сти

26. За­да­ние 14 № 504830. От­ре­зок AC ― диа­метр ос­но­ва­ния ко­ну­са, от­ре­зок AP ― об­ра­зу­ю­щая этого ко­ну­са и AP = AC . Хорда ос­но­ва­ния BC со­став­ля­ет с пря­мой AC угол 60°. Через AP про­ве­де­но се­че­ние ко­ну­са плос­ко­стью, па­рал­лель­ной пря­мой BC. Най­ди­те рас­сто­я­ние от цен­тра ос­но­ва­ния ко­ну­са O до плос­ко­сти се­че­ния, если ра­ди­ус ос­но­ва­ния ко­ну­са равен 1.

27. За­да­ние 14 № 504851. От­ре­зок KM ― диа­метр ос­но­ва­ния ко­ну­са, от­ре­зок AK ― об­ра­зу­ю­щая этого ко­ну­са, ко­то­рая в 3 раза боль­ше ра­ди­у­са его ос­но­ва­ния. Хорда ос­но­ва­ния ML со­став­ля­ет с пря­мой KM угол 45°. Через AK про­ве­де­но се­че­ние ко­ну­са плос­ко­стью, па­рал­лель­ной пря­мой ML. Най­ди­те рас­сто­я­ние от цен­тра ос­но­ва­ния ко­ну­са O до плос­ко­сти се­че­ния, если ра­ди­ус ос­но­ва­ния ко­ну­са равен 1.

28. За­да­ние 14 № 485988. Дана пра­виль­ная че­ты­рех­уголь­ная пи­ра­ми­да Бо­ко­вое ребро сто­ро­на ос­но­ва­ния равна . Най­ди­те рас­сто­я­ние от точки до плос­ко­сти где 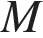— се­ре­ди­на ребра

29. За­да­ние 14 № 485992. Дана пра­виль­ная че­ты­рех­уголь­ная пи­ра­ми­да Бо­ко­вое ребро сто­ро­на ос­но­ва­ния равна Най­ди­те рас­сто­я­ние от точки до плос­ко­сти где 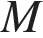— се­ре­ди­на ребра

30. За­да­ние 14 № 504241. Дана пра­виль­ная четырёхуголь­ная пи­ра­ми­да MABCD, рёбра ос­но­ва­ния ко­то­рой равны . Тан­генс угла между пря­мы­ми DM и AL равен , L — се­ре­ди­на ребра MB. Най­ди­те вы­со­ту дан­ной пи­ра­ми­ды.

31. За­да­ние 14 № 501396. Длины ребер и пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да 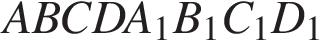равны со­от­вет­ствен­но и Най­ди­те рас­сто­я­ние от вер­ши­ны до пря­мой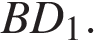

32. За­да­ние 14 № 501416. Длины ребер BC, BB₁ и BA пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да ABCDA₁B₁C₁D₁ равны со­от­вет­ствен­но 8, 12 и 9. Най­ди­те рас­сто­я­ние от вер­ши­ны D₁ до пря­мой A₁C.

33. За­да­ние 14 № 505153. В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC с ос­но­ва­ни­ем ABC бо­ко­вое ребро равно 5, а сто­ро­на ос­но­ва­ния равна 6. Най­ди­те рас­сто­я­ние от вер­ши­ны A до плос­ко­сти SBC.

34. За­да­ние 14 № 500448. В пра­виль­ной ше­сти­уголь­ной приз­ме все рёбра равны . Най­ди­те рас­сто­я­ние от точки до плос­ко­сти .

35. За­да­ние 14 № 484575. В пра­виль­ной ше­сти­уголь­ной приз­ме сто­ро­ны ос­но­ва­ния ко­то­рой равны 3, а бо­ко­вые ребра равны 4, най­ди­те рас­сто­я­ние от точки С до пря­мой .

36. За­да­ние 14 № 484566. В пра­виль­ной ше­сти­уголь­ной приз­ме все ребра ко­то­рой равны най­ди­те рас­сто­я­ние от точки до пря­мой

37. За­да­ние 14 № 484574. Дана пра­виль­ная тре­уголь­ная пи­ра­ми­да DABC с вер­ши­ной D. Сто­ро­на ос­но­ва­ния пи­ра­ми­ды равна , вы­со­та равна . Най­ди­те рас­сто­я­ние от се­ре­ди­ны бо­ко­во­го ребра BD до пря­мой МТ, где точки М и Т — се­ре­ди­ны ребер АС и AВ со­от­вет­ствен­но.

38. За­да­ние 14 № 484572. Дана пра­виль­ная четырёхуголь­ная пи­ра­ми­да с вер­ши­ной Ребро ос­но­ва­ния пи­ра­ми­ды равно вы­со­та — Най­ди­те рас­сто­я­ние от се­ре­ди­ны ребра до пря­мой где точк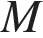и и 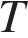 — се­ре­ди­ны ребер и со­от­вет­ствен­но.

39. За­да­ние 14 № 500001. Ос­но­ва­ни­ем пря­мо­го па­рал­ле­ле­пи­пе­да яв­ля­ет­ся ромб ABCD, сто­ро­на ко­то­ро­го равна а угол ВАD равен . Най­ди­те рас­сто­я­ние от точки А до пря­мой , если из­вест­но, что бо­ко­вое ребро дан­но­го па­рал­ле­ле­пи­пе­да равно 8.

40. За­да­ние 14 № 505174. В пра­виль­ной тре­уголь­ной пи­ра­ми­де SABC с ос­но­ва­ни­ем ABC бо­ко­вое ребро равно 3, а сто­ро­на ос­но­ва­ния равна 2. Най­ди­те рас­сто­я­ние от вер­ши­ны A до плос­ко­сти SBC.

41. За­да­ние 14 № 485941. В пра­виль­ной ше­сти­уголь­ной приз­ме все рёбра ко­то­рой равны най­ди­те рас­сто­я­ние от точки до пря­мой

42. За­да­ние 14 № 485955. В пра­виль­ной ше­сти­уголь­ной приз­ме все рёбра ко­то­рой равны 10, най­ди­те рас­сто­я­ние от точки до пря­мой

43. За­да­ние 14 № 505524. Ребро куба ABCDA₁B₁C₁D₁ равно 1. Най­ди­те рас­сто­я­ние от вер­ши­ны B до плос­ко­сти ACD₁.

44. За­да­ние 14 № 485966. В пра­виль­ной че­ты­рех­уголь­ной приз­ме 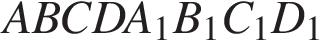вы­со­та равна а сто­ро­на ос­но­ва­ния равна Точка  — се­ре­ди­на ребра Най­ди­те рас­сто­я­ние от точки до плос­ко­сти