Блок 3. Законы Ньютона. Масса. Силы.
Динамика занимается количественным описанием взаимодействия тел
Высказывания Галилея. «Нет действия, нет изменения скорости. Есть действие, есть изменение скорости. Каждому действие есть противодействие.»
И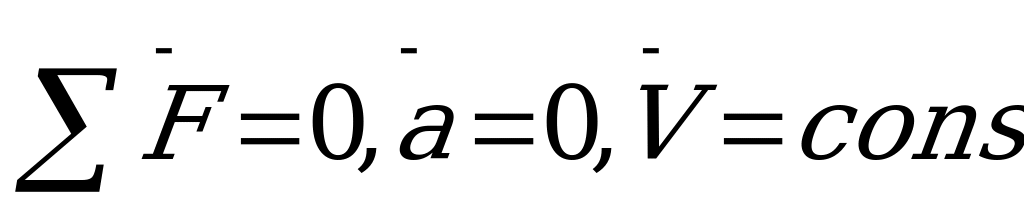 нерция – явление сохранения скорости тел при отсутствии действия со стороны других тел.
нерция – явление сохранения скорости тел при отсутствии действия со стороны других тел.
Первый закон Ньютона: «Тело сохраняет состояние покоя или равномерного
прямолинейного движения, пока на него не действуют другие тела».
5. Сила – физическая величина, характеризующая действие одного теле на другое, в результате которого возникает ускорение, или деформация. Чем больше сила, тем больше ускорение. F = ma. Измеряется в Ньютонах Н
Инертность – свойство тел сопротивляться изменению скорости.
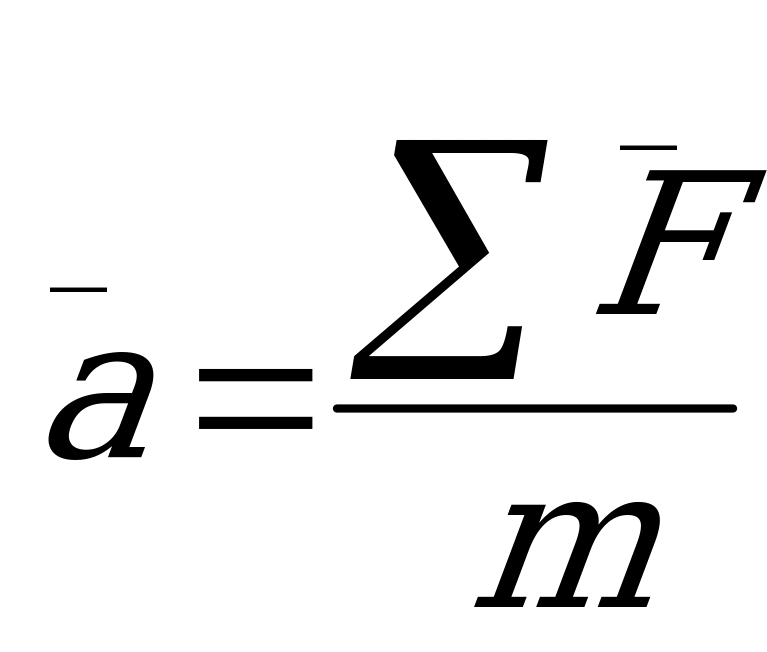 Масса – мера инертности. m = Vρ. Измеряется в кг
Масса – мера инертности. m = Vρ. Измеряется в кг
Зависимость изменения скорости от массы. Чем больше масса, тем меньше изменение скорости.
Равнодействующая сила равна векторной сумме всех, действующих на тело сил.
Второй закон Ньютона: «В инерциальной системе отсчёта ускорение тела прямо
пропорционально равнодействующей силе и обратно пропорционально массе тела». 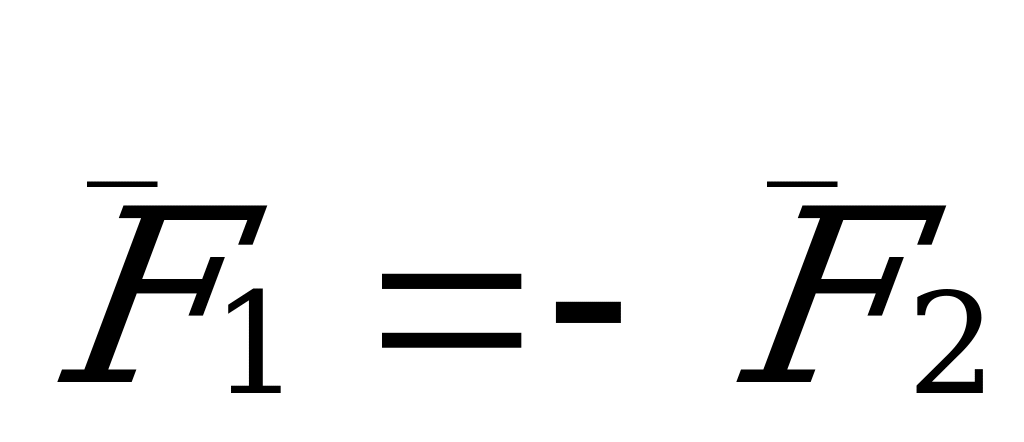
Третий закон Ньютона: «Силы, с которыми два тела действуют друг на друга равны по модулю, противоположны по направлении и действуют вдоль прямой, соединяющей эти тела».
Электромагнитные и гравитационные взаимодействия определяют все механические явления в макромире
Механическая модель кристалла – это упругие молекулы, расположенные в узлах кристаллической решётки. Взаимодействие молекул в кристалле, взаимодействие заряженных частиц, носит электромагнитный характер.
Сила упругости – сила, возникающая при деформации и направлена противоположно смещению частиц при деформации. Fупр= - kx, х – деформация тела, k – жёсткость, которая определяется упругими свойствами тела. Сила упругости – это сила реакции тела на внешнее воздействие. Упругое воздействие на тело – это воздействие, после прекращения которого, тело восстанавливает форму.
Сила нормального давления опоры – N – сила упругости, действующая на тело со стороны опоры, перпендикулярно её поверхности.
Сила натяжения – T – сила упругости, действующая на тело со стороны нити или пружины.
Явление трения – это явление взаимодействия молекул соприкасающихся поверхностей, препятствующее их взаимному перемещению.
Сила трения – сила, возникающая при соприкосновении поверхностей тел, препятствующая их относительному перемещению, направленная вдоль поверхности соприкосновения.
Сила трения покоя – сила, препятствующая возникновению движения одного тела по поверхности другого. (Она всегда по модулю равна силе, приложенной к телу, но противоположна ей по направлению). Максимальная сила трения покоя не зависит от площади соприкосновения и пропорциональна силе нормального давления. (Fmp.n.)max = μп N, где μп – коэффициент трения покоя, который зависит от качества обработки поверхности и сочетания материалов, из которых изготовлены соприкасающиеся тела.
Сила трения скольжения – сила, возникающая при движении и направленная в сторону, противоположную относительной скорости соприкасающихся тел. Она прямо пропорциональна силе нормального давления, но всегда несколько меньше максимальной силе трения покоя. Fmp = μ N
Сила трения качения пропорциональна силе нормального давления и обратно пропорциональна радиусу вращения. Fmp = μкач N/R Коэффициент трения качения во много раз меньше коэффициента трения скольжения, т.к. молекулярные связи разрываются при подъёме колеса гораздо быстрее чем при скольжении.
Трение в газах и в жидкостях обусловлено взаимодействием молекул поверхности тел с молекулами газа или жидкости. Сила трения в газах и в жидкостях прямо пропорциональна скорости движения тел, а при больших скоростях прямо пропорциональна квадрату скорости движения тела. F mp = β V - при малых скоростях и F mp = β V2 - при больших скоростях, где β – коэффициент сопротивления движению в газах и в жидкостях. Он зависит от формы тела, от рода жидкости и площади лобового сечения.
Гравитационные силы. Космические скорости
Гравитационное взаимодействие – это взаимодействие тел, обладающих массой. Масса – мера гравитации. Сила, с которой тела во Вселенной притягиваются друг к другу, прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними F = G M m/R2 –- закон всемирного тяготения .G = 6,67 ∙ 10-11 Нм2/кг2 – гравитационная постоянная, которая показывает, с какой силой два тела массой по 1 кг притягиваются друг к другу на расстоянии 1 м. М - масса тела, которое притягивает к себе другие тела, m – масса тела, которое притягивается, R – расстояние между центрами тел.
Сила тяжести – сила, с которой Земля притягивает к себе тела. На Земле и на различных планетах Fm =mg, где g – ускорение свободного падения на планете. G M m/R2 = mg, отсюда g = G M /R2
Для преодоления силы тяжести телу необходимо сообщить скорости:
7,8 км/сек – 1-я космическая скорость (тело становится спутником Земли).
11,2 км/сек – 2-я космическая скорость (тело становится спутником Солнца). G M m/R2 = mv2/R, v2= G M m/R. Около поверхности Земли v2= R g
42 км/сек – 3-я космическая скорость (тело покидает Солнечную систему).
Вес тела – Вес тела – сила, с которой тело действует на опору (сила нормального давления), или подвес (сила натяжения). Вес тела в случае горизонтального движения на горизонтальной опоре P=mg;
вес тела в случае вертикального движения на горизонтальной опоре или вертикальном подвесе а) движение вверх с ускорением – P = m(g+a), без ускорения - P=mg б) движение вниз с ускорением – P = m(g-a), без ускорения – P = mg.
вес тела, движущегося на негоризонтальной опоре и на невертикальном подвесе
будет всегда по модулю равен силе реакции опоры. P = N = Т
Невесомость. Вес тела равен нулю, когда тело находится в свободном падении, т.е. на него действует только сила тяжести
Перегрузки. Вес тела возрастает в несколько раз.
Н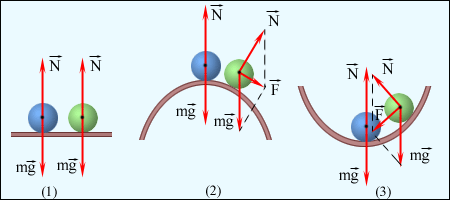 а тело, погружённое в жидкость или газ действует выталкивающая сила, равная весу жидкости или газа в объёме этого тела. F = ρgV. Эта сила называется ещё силой Архимеда, которая действует только в гравитационном поле.
а тело, погружённое в жидкость или газ действует выталкивающая сила, равная весу жидкости или газа в объёме этого тела. F = ρgV. Эта сила называется ещё силой Архимеда, которая действует только в гравитационном поле.
Равновесие тел
Виды равновесия: безразличное, неустойчивое и устойчивое.
Условие равновесия: Тело находится в равновесии, если равнодействующая сила равна нулю. При равновесии сумма проекций на любую координатную ось сил, действующих на тело, равна 0. F1x + F2x + F3x +… = 0, F1y + F2y + F3y +… = 0.
У 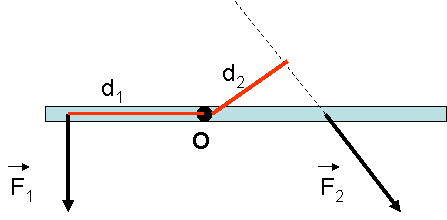 словие равновесия тела, имеющего ось вращения: Тело, имеющее ось вращения, находится в равновесии, если алгебраическая сумма всех моментов сил, действующих на тело, равна 0. Момент силы – величина, равная произведению силы на её плечо. Плечо силы – это кратчайшее расстояние от оси вращения до направления действующей силы. M = Fd – момент силы. M 0, если сила вращает тело по часовой стрелке. M , если сила вращает тело против часовой стрелки.
словие равновесия тела, имеющего ось вращения: Тело, имеющее ось вращения, находится в равновесии, если алгебраическая сумма всех моментов сил, действующих на тело, равна 0. Момент силы – величина, равная произведению силы на её плечо. Плечо силы – это кратчайшее расстояние от оси вращения до направления действующей силы. M = Fd – момент силы. M 0, если сила вращает тело по часовой стрелке. M , если сила вращает тело против часовой стрелки.
4. Все простые механизмы: рычаг, блок, ворот, наклонная плоскость, клин, винт не дают выигрыша в работе: во сколько раз мы выигрываем в силе, во столько раз проигрываем в расстоянии. Это «Золотое правило механики».
Решение задач:
Алгоритм решения задач по динамике
Определить характер и направление движения.
Сделать рисунок с указанием системы отсчёта и сил, действующих на тело.
Записать второй закон Ньютона в векторной форме.
Найти проекции векторных величин и записать второй закон Ньютона в проекциях.
Дописать недостающие величины.
Решить систему уравнений относительно неизвестной величины.
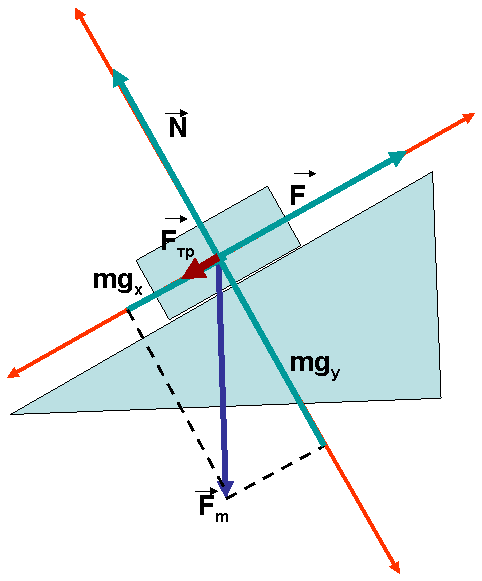
Задача 1. На наклонной плоскости длиной 5 м и высотой 3м находится груз массой 50 кг. Коэффициент трения груза о поверхность 0,2. Какую силу, направленную вдоль плоскости нужно приложить, чтобы а) равномерно втащить его наверх;
б) втащить с ускорением 1м/с2
в) какой путь пройдёт груз вверх по наклонной плоскости
если в начале ему сообщить скорость 2м/с? Трение не учитывать.
Решение
а) ΣFx = 0, Fx + mgx + Fтрx = 0, Fx =F, mgx = - mg sinφ, sinφ =h/L, Nx = 0, Fтрx= - μN, F - mg sinφ - μN = 0
ΣFy = 0, Ny + mgy = 0, mgy = - mg cosφ, cosφ =a/L, a2=L2 - h2, N = mg cosφ,
б) ΣFx = max, Fx + mgx + Fтрx = max, Fx =F, mgx = - mg sinφ, sinφ =h/L, Nx = 0, Fтрx= - μN, ax = a, F - mg sinφ - μN = ma
ΣFy = 0, Ny + mgy = 0, mgy = -mg cosφ, cosφ =a/L, a2=L2 + h2, Ny = N = mg cosφ
в) ΣFx = max, mgx + Fтрx = max, mgx = - mg sinφ, sinφ =h/L, Nx = 0, Fтрx= - μmg cosφ, ax = a. mg sinφ - μmg cosφ = ma, а = (mg sinφ - μmg cosφ)/ m, S = v2/2a.
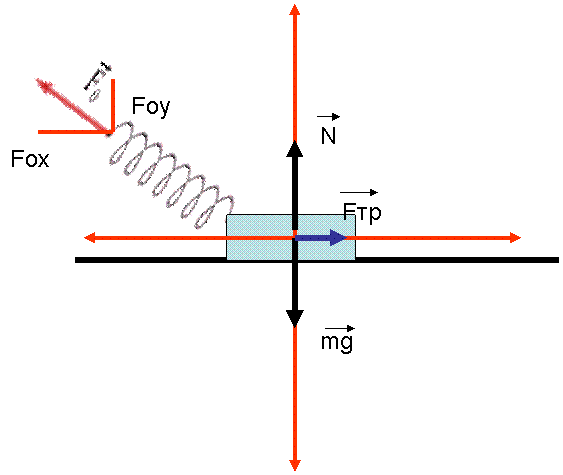
Задача 2. Деревянный брусок массой 2 кг равномерно тянут по деревянной доске, расположенной горизонтально с помощью пружины жёсткостью 100н/м. Пружина наклонена под углом 30 градусов к плоскости. Коэффициент трения равен 0,3. Найти удлинение пружины. Найти силу упругости. Найти силу нормального давления бруска на поверхность.
Решение
а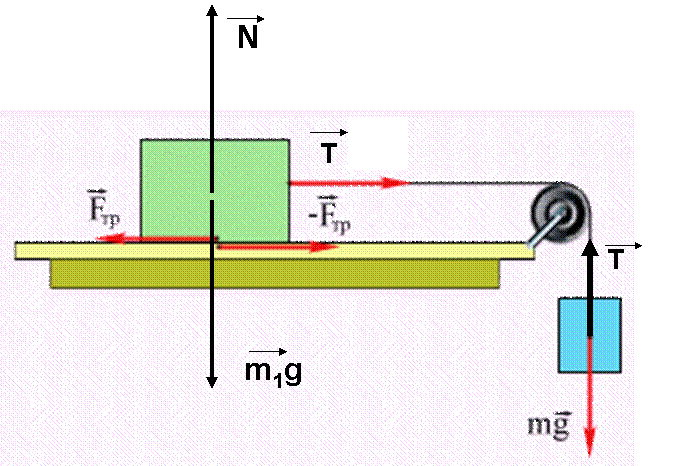 ) ΣFx = 0, Fx + mgx + Fтрx = 0, F = kx, Fx = kxcosφ, mgx = - 0, Nx= 0, Fтрx= - μN. ΣFy = 0, Fy +Ny + mgy = 0, F = kx, Fy = kxsinφ, mgy = - mg , Ny = N.
) ΣFx = 0, Fx + mgx + Fтрx = 0, F = kx, Fx = kxcosφ, mgx = - 0, Nx= 0, Fтрx= - μN. ΣFy = 0, Fy +Ny + mgy = 0, F = kx, Fy = kxsinφ, mgy = - mg , Ny = N.
Задача 3. Брусок массой 400 г, находящийся на столе начинает двигаться под действием груза массой 100 г и за две секунды проходит 80 см. 1. Найти силу трения и коэффициент трения.
2. С каким ускорением движутся бруски?
3. Найти силу натяжения нити.
(для самостоятельного решения).
З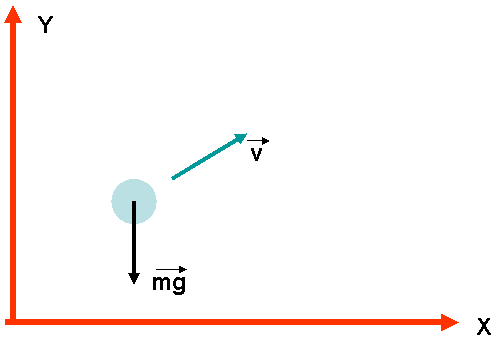 адача 4. На рисунке указано направление скорости
адача 4. На рисунке указано направление скорости
движущегося тела и силы, действующей на него.
1. Укажите направление ускорения тела.
2. По какой траектории движется тело? Почему?
3. Когда тело будет находиться в состоянии невесомости:
на подъёме,
на спуске,
в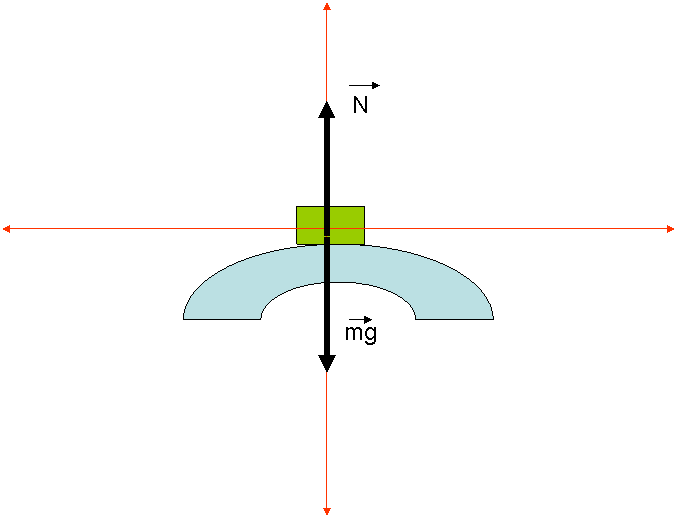 верхней точке траектории.
верхней точке траектории.
в любой точке траектории.
Решение
Ускорение имеет такое же направление, как и вектор силы тяжести.
Если скорость тела направлена под углом к горизонту и на тело действует только сила тяжести, то тело движется по параболе.
Тело будет находиться в состоянии невесомости всё время движения.
Р
З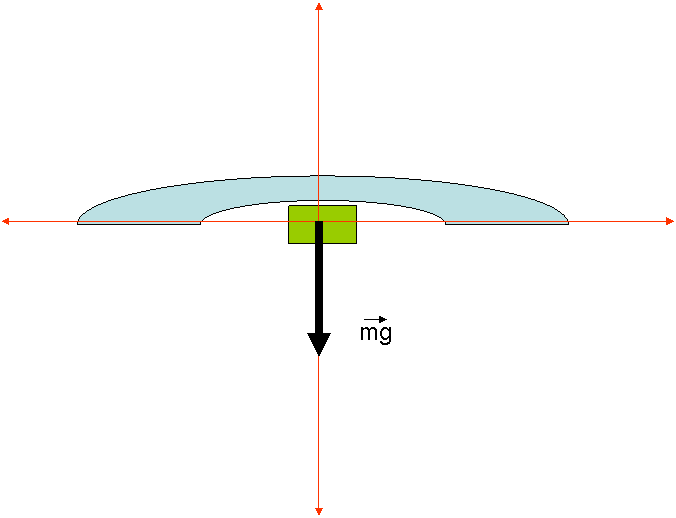 адача 5. Автомобиль массой 2 тонны проходит по выпуклому мосту, имеющему радиус кривизны 40 м. ср скоростью 36 км /час. С какой силой автомобиль давит на мост в его середине.? С какой скоростью должен двигаться автомобиль, чтобы в середине моста водитель оказался в состоянии невесомости?
адача 5. Автомобиль массой 2 тонны проходит по выпуклому мосту, имеющему радиус кривизны 40 м. ср скоростью 36 км /час. С какой силой автомобиль давит на мост в его середине.? С какой скоростью должен двигаться автомобиль, чтобы в середине моста водитель оказался в состоянии невесомости?
Решение: Ny+ mgy = may. Ny = -N, mgy = mg, ay = v2/R, Py = - Ny
Задача 7. С какой минимальной скоростью может двигаться мотоциклист под куполом цирка по траектории, радиус которой 160 м.
(для самостоятельного решения)
Формулы динамики
Законы Ньютона
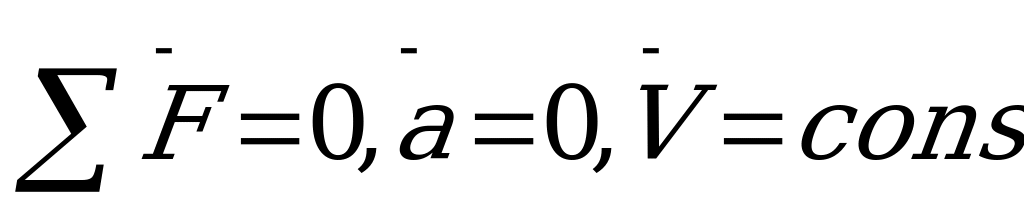
1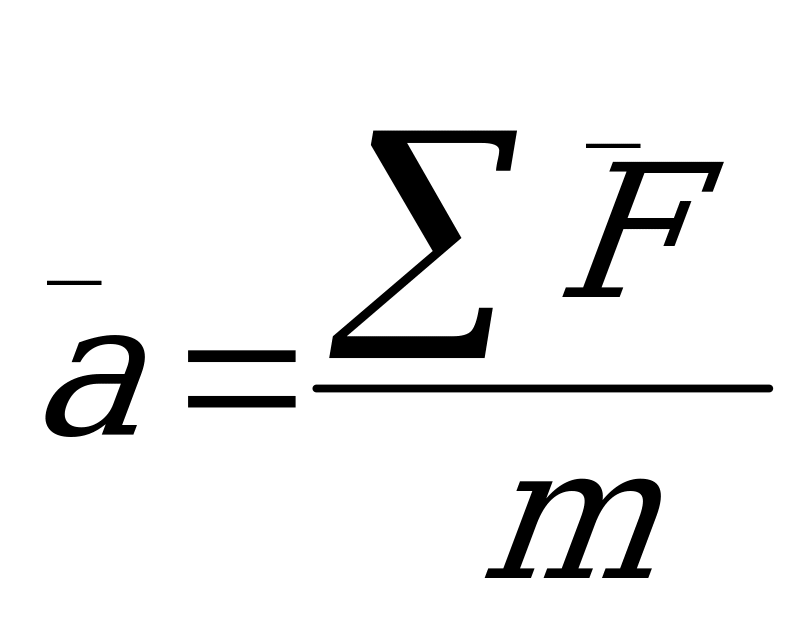
2
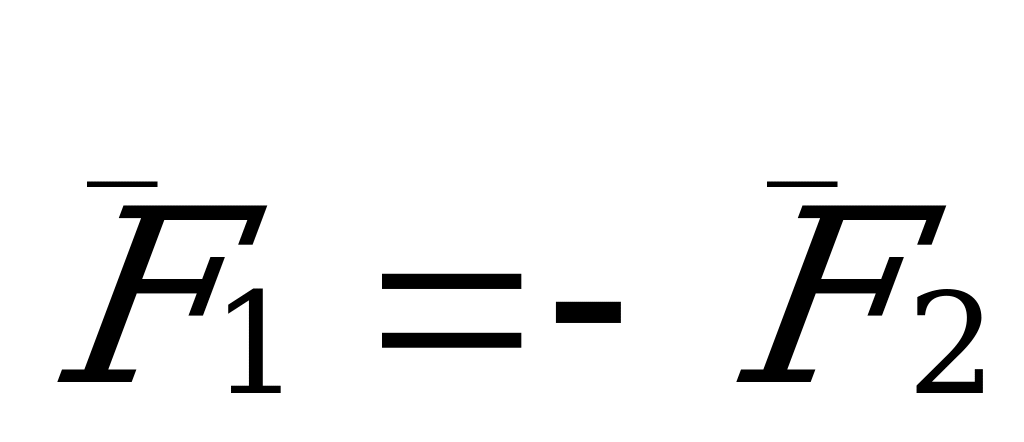
3
Силы природы
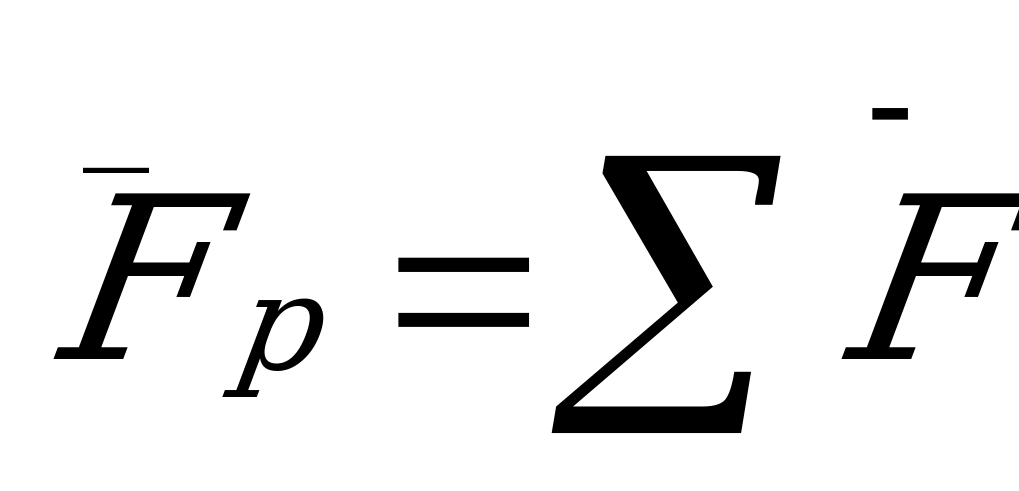
- равнодействующая сила
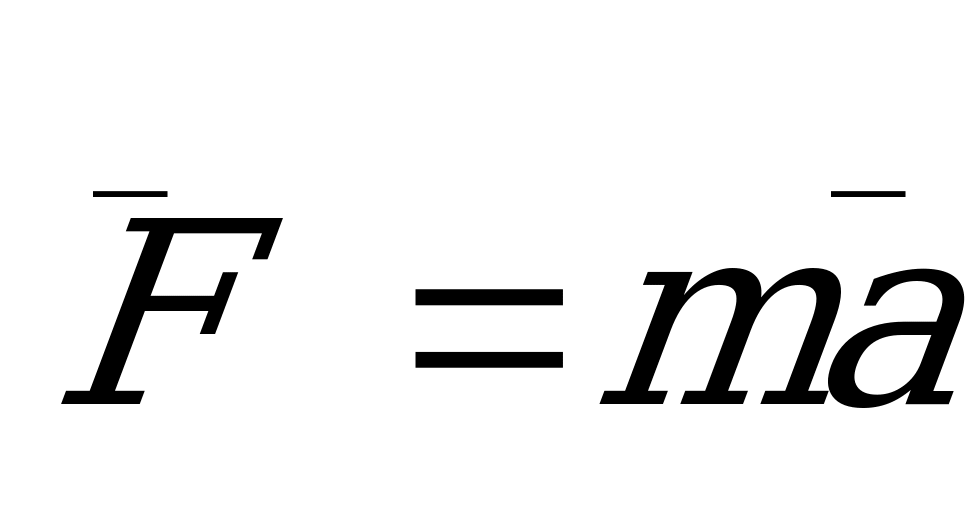
- ньютоновская сила
Fm =mg - сила тяжести, g = G M /R2 – ускорение свободного падения
Fтр = μ N - сила трения
Fупр= - kx - сила упругости
Fтр = β υ - сила трения в жидкостях и газах при малых скоростях
Fтр = β υ 2 - сила трения в жидкостях и газах при больших скоростях F = G M m/R2 – сила всемирного тяготения
v2= G M m/R - 1-я косм. скорость. Около поверхности Земли v2= R g
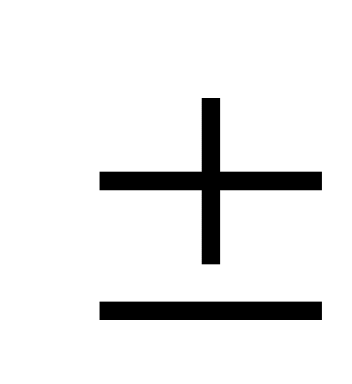 P = m(g a) - вес тела
P = m(g a) - вес тела
F = ρgV – сила Архимеда.
m = Vρ – масса тела.
F1x + F2x + F3x +… = 0, F1y + F2y + F3y +… = 0 – условие равновесия тела.
M = Fd – момент силы. M 0, если сила вращает тело по часовой стрелке. M
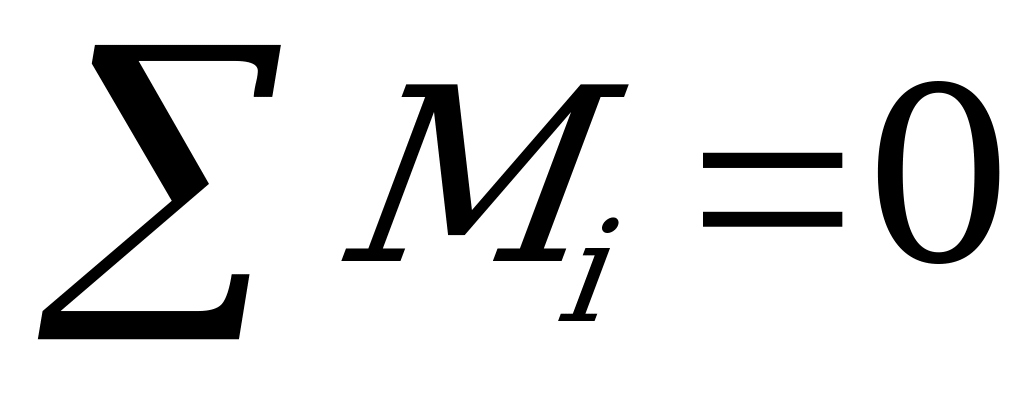
- условие равновесия тела, имеющего ось вращения
2
Динамика прямолинейного движения. Z. Rodchenko







 а тело, погружённое в жидкость или газ действует выталкивающая сила, равная весу жидкости или газа в объёме этого тела. F = ρgV. Эта сила называется ещё силой Архимеда, которая действует только в гравитационном поле.
а тело, погружённое в жидкость или газ действует выталкивающая сила, равная весу жидкости или газа в объёме этого тела. F = ρgV. Эта сила называется ещё силой Архимеда, которая действует только в гравитационном поле. словие равновесия тела, имеющего ось вращения: Тело, имеющее ось вращения, находится в равновесии, если алгебраическая сумма всех моментов сил, действующих на тело, равна 0. Момент силы – величина, равная произведению силы на её плечо. Плечо силы – это кратчайшее расстояние от оси вращения до направления действующей силы. M = Fd – момент силы. M 0, если сила вращает тело по часовой стрелке. M , если сила вращает тело против часовой стрелки.
словие равновесия тела, имеющего ось вращения: Тело, имеющее ось вращения, находится в равновесии, если алгебраическая сумма всех моментов сил, действующих на тело, равна 0. Момент силы – величина, равная произведению силы на её плечо. Плечо силы – это кратчайшее расстояние от оси вращения до направления действующей силы. M = Fd – момент силы. M 0, если сила вращает тело по часовой стрелке. M , если сила вращает тело против часовой стрелки.

 ) ΣFx = 0, Fx + mgx + Fтрx = 0, F = kx, Fx = kxcosφ, mgx = - 0, Nx= 0, Fтрx= - μN. ΣFy = 0, Fy +Ny + mgy = 0, F = kx, Fy = kxsinφ, mgy = - mg , Ny = N.
) ΣFx = 0, Fx + mgx + Fтрx = 0, F = kx, Fx = kxcosφ, mgx = - 0, Nx= 0, Fтрx= - μN. ΣFy = 0, Fy +Ny + mgy = 0, F = kx, Fy = kxsinφ, mgy = - mg , Ny = N. адача 4. На рисунке указано направление скорости
адача 4. На рисунке указано направление скорости  верхней точке траектории.
верхней точке траектории. адача 5. Автомобиль массой 2 тонны проходит по выпуклому мосту, имеющему радиус кривизны 40 м. ср скоростью 36 км /час. С какой силой автомобиль давит на мост в его середине.? С какой скоростью должен двигаться автомобиль, чтобы в середине моста водитель оказался в состоянии невесомости?
адача 5. Автомобиль массой 2 тонны проходит по выпуклому мосту, имеющему радиус кривизны 40 м. ср скоростью 36 км /час. С какой силой автомобиль давит на мост в его середине.? С какой скоростью должен двигаться автомобиль, чтобы в середине моста водитель оказался в состоянии невесомости?









