Задание 1 № 101. Может ли график зависимости пути от времени иметь следующий вид?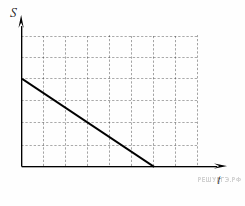
1) да
2) нет
3) может, если траектория прямолинейная
4) может, если тело возвращается в исходную точку
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. По определению, путь есть величина положительная, которая может только возрастать со временем, так что представленный график не может изображать зависимость пути от времени.
Правильный ответ: 2.
Задание 1 № 125. Вертолет поднимается вертикально вверх. Какова траектория движения точки на конце лопасти винта вертолета в системе отсчета, связанной с винтом?
1) точка
2) прямая
3) окружность
4) винтовая линия
Решение.
В системе отсчета, связанной с винтом, точка на конце лопасти не двигается. Следовательно, ее траектория в данной системе отсчета представляет собой точку.
Правильный ответ: 1.
Задание 1 № 126. Два автомобиля движутся по прямому шоссе: первый — со скоростью ν, второй — со скоростью -3 ν. Какова скорость второго автомобиля относительно первого?
Решение.
Скорость второго автомобиля относительно первого равна ν2 - ν 1=-3 ν- ν= -4ν
Правильный ответ: 2.
Задание 1 № 131. Лодка должна попасть на противоположный берег реки по кратчайшему пути в системе отсчета, связанной с берегом. Скорость течения реки u, а скорость лодки относительно воды ν . Чему должен быть равен модуль скорости лодки относительно берега?
1) ![]()
2) ![]()
3) ![]()
4) ![]()
Решение.
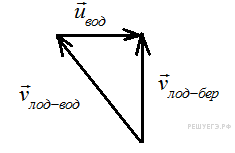 1 способ: По закону сложения скоростей, вектор скорости лодки относительно берега (неподвижной с.о.) равен сумме скорости лодки относительно воды (подвижной с.о.) и скорости течения воды (переносной скорости). По условию, вектор скорости лодки в системе отсчета, связанной с берегом, должен быть перпендикулярен ему. Построив «треугольник скоростей» из теоремы Пифагора для скорости лодки относительно берега имеем
1 способ: По закону сложения скоростей, вектор скорости лодки относительно берега (неподвижной с.о.) равен сумме скорости лодки относительно воды (подвижной с.о.) и скорости течения воды (переносной скорости). По условию, вектор скорости лодки в системе отсчета, связанной с берегом, должен быть перпендикулярен ему. Построив «треугольник скоростей» из теоремы Пифагора для скорости лодки относительно берега имеем
![]()
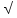 ν2 - u2
ν2 - u2
2 способ:
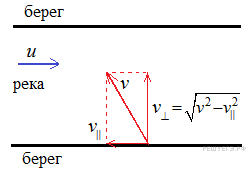 Вектор скорости лодки относительно воды разложим на две компоненты:
Вектор скорости лодки относительно воды разложим на две компоненты: ![]() , где вектор
, где вектор ![]() направлен параллельно берегу, а вектор
направлен параллельно берегу, а вектор ![]() — перпендикулярно берегу. Для того, чтобы лодка в системе отсчета, связанной с берегом, двигалась перпендикулярно к нему, необходимо, чтобы компонента скорости лодки относительно воды вдоль реки
— перпендикулярно берегу. Для того, чтобы лодка в системе отсчета, связанной с берегом, двигалась перпендикулярно к нему, необходимо, чтобы компонента скорости лодки относительно воды вдоль реки ![]() в точности компенсировала скорость течения u. Тогда модуль скорости лодки относительно берега будет равен (по теореме Пифагора)
в точности компенсировала скорость течения u. Тогда модуль скорости лодки относительно берега будет равен (по теореме Пифагора)
![]()
Правильный ответ: 4.
Задание 1 № 133. На рисунке представлен график зависимости пути S велосипедиста от времени t.
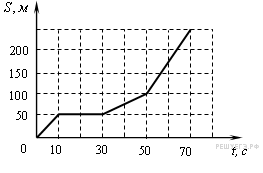
Определите интервал времени после начала отсчета времени, когда велосипедист двигался со скоростью 5 м/с.
1) от 50 с до 70 с
2) от 30 с до 50 с
3) от 10 с до 30 с
4) от 0 до 10 с
Решение.
Для того чтобы по графику зависимости пути от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Из графика видно, что в интервале от 0 до 10 с скорость велосипедиста была постоянна и равнялась
![]() .
.
На других интервалах скорость была иная.
Правильный ответ: 4.
Задание 1 № 134. На рисунке представлен график движения автобуса из пункта A в пункт Б и обратно.
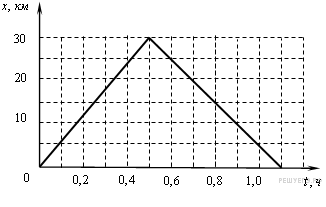
Пункт A находится в точке х=0, а пункт Б — в точке х=30 км. Чему равна максимальная скорость автобуса на всем пути следования туда и обратно? (Ответ дайте в километрах в час.)
Решение.
Для того чтобы по графику зависимости координаты от времени найти скорость движения тела в некоторый момент, необходимо вычислить тангенс угла наклона графика в соответствующей точке. Максимальной скорости соответствует максимальный угол наклона. Из приведенного графика видно, что с максимальной скоростью автобус движется из пункта A в пункт Б, скорость его при этом равна: 30-0/0,5=60 км/ч.
Задание 1 № 138. На рисунке приведен график зависимости проекции скорости тела от времени.
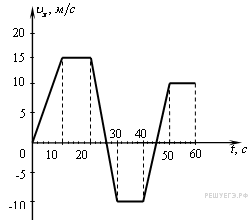
Чему равно ускорение тела в интервале времени от 30 до 40 с? (Ответ дайте в метрах в секунду в квадрате.)
Решение.
Из графика видно, что в интервале времени от 30 до 40 с проекция скорости тела не изменялась, а значит, проекция ускорения была равна нулю.
Задание 1 № 317. Пловец плывет по течению реки. Определите скорость пловца относительно берега, если скорость пловца относительно воды 0,4 м/с, а скорость течения реки 0,3 м/с. (Ответ дайте в метрах в секунду.)
Решение.
Вектор скорости пловца относительно берега есть сумма векторов скорости пловца относительно воды и скорости течения реки:. Поскольку пловец плывет по течению реки, получаем, что для величин скоростей выполняется соотношение: 0,4 + 0,3 =0,7 м/с.
Задание 1 № 3354. Четыре тела двигались по оси Ох. В таблице представлена зависимость их координат от времени.
| t, с | 0 | 1 | 2 | 3 | 4 | 5 |
| x1, м. | 0 | 2 | 4 | 6 | 8 | 10 |
| x2, м | 0 | 0 | 0 | 0 | 0 | 0 |
| x3, м | 0 | 1 | 4 | 9 | 16 | 25 |
| x4, м | 0 | 2 | 0 | -2 | 0 | 2 |
У какого из тел скорость могла быть постоянна и отлична от нуля?
Решение.
Таблица содержит информацию о положениях тел только в отдельные моменты времени. В промежутках между указанными временами тела могли двигаться абсолютно произвольно. Определим тело, скорость которого могла бы быть постоянной и отличной от нуля. При движении с постоянной скоростью координата тела за равные промежутки времени изменяется одинаково. Из таблицы видно, что этому свойству удовлетворяет только первое тело. Значит, скорость первого тела могла быть постоянной и не равной нулю.
Задание 1 № 3357. Вертолет равномерно поднимается вертикально вверх. Какова траектория крайней точки лопасти вертолета в системе отсчета, связанной с корпусом вертолета?
1) прямая линия
2) винтовая линия
3) окружность
4) эллипс
Решение.
Крайняя точка лопасти вертолета двигается по окружности вокруг оси вращения винта. Поскольку ось вращения жестко связана с корпусом вертолета, такую же траекторию описывает эта точка и относительно любой точки корпуса. Правильный ответ 3.
Задание 1 № 3539. На каком из графиков изображена возможная зависимость пройденного пути от времени?
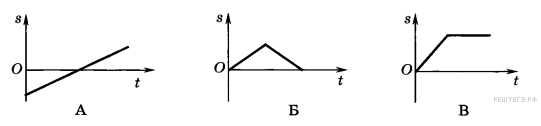
1) А
2) Б
3) В
4) Такой график отсутствует
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. По определению, путь есть величина положительная, которая может только возрастать со временем. Этому требованию удовлетворяет только график В.
Правильный ответ: 3.
Задание 1 № 3540. Велосипедист, двигаясь под уклон, проехал расстояние между двумя пунктами со скоростью, равной 15 км/ч. Обратно он ехал вдвое медленнее. Какова средняя путевая скорость на всем пути? (Ответ дайте в километрах в час.)
Решение.
Необходимо различать два понятия: среднюю путевую скорость и среднюю скорость по перемещению. Средняя путевая скорость определяется как скорость прохождения пути: ![]() . То есть, буквально, надо весь пройденный телом путь разделить на все время, затраченное им на этот путь. Средняя путевая скорость представляет собой число, скаляр.
. То есть, буквально, надо весь пройденный телом путь разделить на все время, затраченное им на этот путь. Средняя путевая скорость представляет собой число, скаляр.
Разберемся теперь со второй средней скоростью. Средняя скорость по перемещению — это вектор, равный отношению перемещения ко времени, за которое оно совершено: ![]() . В нашей конкретной задаче, поскольку велосипедист вернулся в исходную точку, его перемещение равно нулю, а значит, его средняя скорость по перемещению тоже равна нулю.
. В нашей конкретной задаче, поскольку велосипедист вернулся в исходную точку, его перемещение равно нулю, а значит, его средняя скорость по перемещению тоже равна нулю.
Вычислим теперь среднюю путевую скорость. Обозначим расстояние между двумя пунктами через ![]() ? тогда весь путь пройденный велосипедистом равен
? тогда весь путь пройденный велосипедистом равен ![]() . На первую половину пути велосипедист затратил время
. На первую половину пути велосипедист затратил время ![]() . На обратную дорогу — время
. На обратную дорогу — время ![]() . Все время пути составило
. Все время пути составило ![]() . Окончательно, находим, что средняя путевая скорость велосипедиста равна
. Окончательно, находим, что средняя путевая скорость велосипедиста равна
![]() .
.
Задание 1 № 3541. Тело движется прямолинейно вдоль оси x. На графике представлена зависимость координаты тела от времени. В какой момент времени модуль перемещения относительно исходной точки имел максимальное значение? (Ответ дайте в секундах.)
Решение.
Из графика видно, что начальная координата тела равна ![]() . Модуль перемещения тела относительно исходной точки в любой момент определяется выражением:
. Модуль перемещения тела относительно исходной точки в любой момент определяется выражением: ![]() . Построим график этой функции и определим ее максимум. Из построенного графика ясно, что модуль перемещения относительно исходной точки максимален при
. Построим график этой функции и определим ее максимум. Из построенного графика ясно, что модуль перемещения относительно исходной точки максимален при ![]() и равен 20 м.
и равен 20 м.
Ответ: 6 с
Задание 1 № 3544. Движение двух велосипедистов заданы уравнениями x1 =2 t и x2 =100- 8 t . Найдите координату x места встречи велосипедистов. Велосипедисты двигаются вдоль одной прямой. (Ответ дайте в метрах.)
Решение.
Встреча двух велосипедистов означает, что у них в некоторый момент времени совпадут координаты. Определим, когда именно произойдет встреча, для этого решим уравнение ![]() . Теперь не составляет труда определить координату места встречи:
. Теперь не составляет труда определить координату места встречи:
![]()
Задание 1 № 3545.
На рисунке приведен график движения x(t) электрокара. Определите по этому графику путь, проделанный электрокаром за интервал времени от t1 = 1 c до t2 = 4 c. (Ответ дайте в метрах.)
Решение.
Путь — это физическая величина, показывающая пройденное телом расстояние. Иначе говоря, это длина пройденного участка траектории. Из графика видно, что в интервале времени от ![]() до
до ![]() электрокар двигался в положительном направлении оси
электрокар двигался в положительном направлении оси ![]() . При этом его координата изменилась на
. При этом его координата изменилась на ![]() . Последнюю, четвертую, секунду электрокар двигался в обратном направлении, изменение его координаты на этом участке равно
. Последнюю, четвертую, секунду электрокар двигался в обратном направлении, изменение его координаты на этом участке равно ![]() . Таким образом, путь, пройденный машинкой за интервал времени от
. Таким образом, путь, пройденный машинкой за интервал времени от ![]() до
до ![]() равен
равен ![]() .
.
Задание 1 № 3548. Пешеход идет по прямолинейному участку дороги со скоростью v. Навстречу ему движется автобус со скоростью 10v. С какой скоростью должен двигаться навстречу пешеходу велосипедист, чтобы модуль его скорости относительно пешехода и автобуса был одинаков?
1) ![]()
2) ![]()
3) ![]()
4) ![]()
Решение.
Обозначим искомую скорость велосипедиста через ![]() . Тогда, как видно из рисунка, велосипедист приближается к пешеходу со скоростью
. Тогда, как видно из рисунка, велосипедист приближается к пешеходу со скоростью ![]() , а к автобусу — со скоростью
, а к автобусу — со скоростью ![]() .
.
Приравняв эти две скорости, находим требуемую скорость велосипедиста: ![]()
Правильный ответ: 1.
Задание 1 № 3549. Пароход движется по реке против течения со скоростью 5 м/с относительно берега. Определите скорость течения реки, если скорость парохода относительно берега при движении в обратном направлении равна 8 м/с. (Ответ дайте в метрах в секунду.)
Решение.
Обозначим искомую скорость течения реки через ![]() , а скорость парохода в стоячей воде — через
, а скорость парохода в стоячей воде — через ![]() . Тогда можно составить следующие уравнения. Скорость парохода вниз по течению равна
. Тогда можно составить следующие уравнения. Скорость парохода вниз по течению равна ![]() . Скорость парохода вверх по течению:
. Скорость парохода вверх по течению: ![]() . Решая систему из двух этих уравнений, для скорости течения воды имеем
. Решая систему из двух этих уравнений, для скорости течения воды имеем ![]() .
.
Задание 1 № 3734.
Материальная точка движется вдоль оси OX. На рисунке представлен график зависимости проекции скорости этой материальной точки на ось OX от времени. Какой из приведенных ниже графиков может соответствовать зависимости координаты материальной точки от времени?
1) 1
2) 2
3) 3
4) 4
Решение.
Из графика видно, что проекция скорости материальной точки на ось OX положительна и постоянна, а значит, точка движется равномерно и в положительном направлении оси OX. Единственный график, удовлетворяющий обоим этим требованиям, — это график под номером 1.
Правильный ответ: 1.
Задание 1 № 3783. На рисунке представлены графики зависимости пройденного пути от времени для двух тел. На какую величину Δv скорость второго тела v2 больше скорости первого тела v1? (Ответ дайте в метрах в секунду.)
Решение.
Из графика видно, что для обоих тел пройденный путь линейно зависит от времени, а значит, оба тела двигались с постоянными по величине скоростями. Модуль скорости первого тела равен ![]() . Скорость же второго тела:
. Скорость же второго тела: ![]() . Следовательно, скорость второго тела больше скорости первого тела на величину
. Следовательно, скорость второго тела больше скорости первого тела на величину ![]()
Задание 1 № 3867.
Тела 1 и 2 двигаются вдоль оси x. На рисунке изображены графики зависимости координат движущихся тел 1 и 2 от времени t. Чему равен модуль скорости 1 относительно тела 2? (Ответ дайте в метрах в секунду.)
Решение.
Используя график, определим проекции скоростей обоих тел. Для тела 1 имеем
![]()
Для тела 2:
![]()
Таким образом модуль скорости одного тела относительно другого равен
![]()
Задание 1 № 4077. Автобус везёт пассажиров по прямой дороге со скоростью 10 м/с. Пассажир равномерно идёт по салону автобуса со скоростью 1 м/с относительно автобуса, двигаясь от задней двери к кабине водителя. Чему равен модуль скорости пассажира относительно дороги? (Ответ дайте в метрах в секунду.)
Решение.
Согласно закону сложения скоростей, скорость тела относительно «неподвижной системы отсчёта» ![]() связана со скоростью этого тела относительно «подвижной системы отсчёта»
связана со скоростью этого тела относительно «подвижной системы отсчёта» ![]() и скоростью движения «подвижной с. о.» относительно «неподвижной»
и скоростью движения «подвижной с. о.» относительно «неподвижной» ![]() при помощи следующего соотношения:
при помощи следующего соотношения: ![]() В данном случае, так как пассажир двигается вдоль автобуса по направлению его движения, для скорости пассажира относительно дороги имеем:
В данном случае, так как пассажир двигается вдоль автобуса по направлению его движения, для скорости пассажира относительно дороги имеем: ![]()
Ответ: 11 м/с
Задание 1 № 4186. Координата ![]() материальной точки изменяется с течением времени
материальной точки изменяется с течением времени ![]() по закону x=3-2t. Какой из приведённых ниже графиков соответствует этой зависимости?
по закону x=3-2t. Какой из приведённых ниже графиков соответствует этой зависимости?
1) 1
2) 2
3) 3
4) 4
Решение.
Из зависимости ![]() видно, что координата убывает со временем, при этом в начальный момент времени координата равна
видно, что координата убывает со временем, при этом в начальный момент времени координата равна ![]() а в начало координат материальная точка попадает в момент времени:
а в начало координат материальная точка попадает в момент времени: ![]() Таким образом, зависимости
Таким образом, зависимости ![]() соответствует график под номером 4.
соответствует график под номером 4.
Правильный ответ: 4.
Задание 1 № 4221. Координата ![]() материальной точки изменяется с течением времени
материальной точки изменяется с течением времени ![]() по закону . x=3+ 2t. Какой из приведённых ниже графиков соответствует этой зависимости?
по закону . x=3+ 2t. Какой из приведённых ниже графиков соответствует этой зависимости?
1)
2)
3)
4)
Решение.
Из зависимости ![]() видно, что координата возрастает со временем, при этом в начальный момент времени координата равна
видно, что координата возрастает со временем, при этом в начальный момент времени координата равна ![]() , а в момент времени
, а в момент времени ![]() координата равна
координата равна ![]() . Таким образом, зависимости
. Таким образом, зависимости ![]() соответствует график под номером 3.
соответствует график под номером 3.
Правильный ответ: 3.
Задание 1 № 4409. По плоскости ![]() движутся четыре точечных тела —А, Б, В, Г. x=1+t., y=2 t,
движутся четыре точечных тела —А, Б, В, Г. x=1+t., y=2 t, ![]() и
и ![]() , траектории которых изображены на рисунке. Зависимости координат одного из этих тел от времени имеют вид
, траектории которых изображены на рисунке. Зависимости координат одного из этих тел от времени имеют вид ![]() и
и ![]() . Это тело обозначено буквой
. Это тело обозначено буквой
1) А
2) Б
3) В
4) Г
Решение.
На зависимость координат от времени ![]() и
и ![]() можно смотреть как на параметрическое задание прямой на плоскости
можно смотреть как на параметрическое задание прямой на плоскости ![]() .
.
Выразим время ![]() из первого уравнения
из первого уравнения ![]() и подставим во второе:
и подставим во второе: ![]() . Из рисунка видно, что уравнению
. Из рисунка видно, что уравнению ![]() соответствует прямая
соответствует прямая ![]() .
.
Правильный ответ: 3
Задание 1 № 4444. По плоскости ![]() движутся четыре точечных тела — А,Б
движутся четыре точечных тела — А,Б ![]() В,
В, ![]() и Г
и Г![]() , траектории которых изображены на рисунке. Зависимости координат одного из этих тел от времени имеют вид x=2t.и . y=1+ t. Это тело обозначено буквой
, траектории которых изображены на рисунке. Зависимости координат одного из этих тел от времени имеют вид x=2t.и . y=1+ t. Это тело обозначено буквой
1) А
2) Б
3) В
4) Г
Решение.
На зависимость координат от времени ![]() и
и ![]() можно смотреть как на параметрическое задание прямой на плоскости
можно смотреть как на параметрическое задание прямой на плоскости ![]() .
.
Выразим время ![]() из первого уравнения
из первого уравнения ![]() и подставим во второе:
и подставим во второе: ![]() . Из рисунка видно, что уравнению
. Из рисунка видно, что уравнению ![]() соответствует прямая A.
соответствует прямая A.
Правильный ответ: 1
Задание 1 № 4934. Два автомобиля движутся по прямому шоссе: первый со скоростью ![]() , второй со скоростью
, второй со скоростью ![]() относительно шоссе. Скорость первого автомобиля относительно второго равна
относительно шоссе. Скорость первого автомобиля относительно второго равна
1) ![]()
2) ![]()
3) ![]()
4) ![]()
Решение.
Скорость первого автомобиля относительно второго равна
![]() .
.
Правильный ответ: 2.






 1 способ: По закону сложения скоростей, вектор скорости лодки относительно берега (неподвижной с.о.) равен сумме скорости лодки относительно воды (подвижной с.о.) и скорости течения воды (переносной скорости). По условию, вектор скорости лодки в системе отсчета, связанной с берегом, должен быть перпендикулярен ему. Построив «треугольник скоростей» из теоремы Пифагора для скорости лодки относительно берега имеем
1 способ: По закону сложения скоростей, вектор скорости лодки относительно берега (неподвижной с.о.) равен сумме скорости лодки относительно воды (подвижной с.о.) и скорости течения воды (переносной скорости). По условию, вектор скорости лодки в системе отсчета, связанной с берегом, должен быть перпендикулярен ему. Построив «треугольник скоростей» из теоремы Пифагора для скорости лодки относительно берега имеем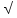 ν2 - u2
ν2 - u2 Вектор скорости лодки относительно воды разложим на две компоненты:
Вектор скорости лодки относительно воды разложим на две компоненты: 























