Задание 15 (презентация по типам задач к ЕГЭ)

Ege 15

(повышенный уровень, время – 3 мин)

обозначает число путей из вершины A в некоторую вершину Q

Тема : Графы. Поиск количества путей

Что нужно знать :

• если в город R можно приехать только из городов X, Y , и Z , то число различных путей из города A в город R равно сумме числа различных путей проезда из A в X , из A в Y и из A в Z , то есть

, где

• число путей конечно, если в графе нет циклов – замкнутых путей

Пример I:

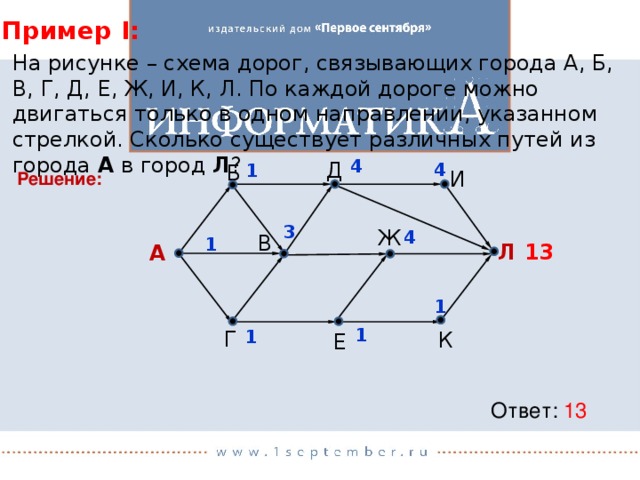
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, Л. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Л ?

4

Д

4

1

Б

Решение:

И

3

Ж

4

13

В

1

Л

А

1

1

1

Г

К

Е

Ответ: 13

Пример II:

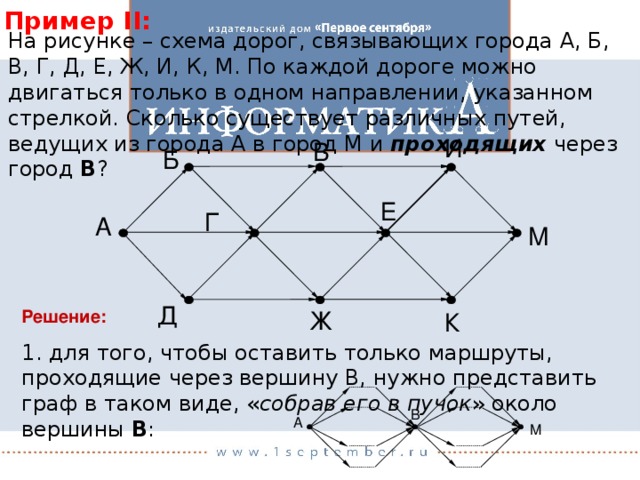
На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей, ведущих из города А в город М и проходящих через город В ?

И

B

Б

Е

Г

А

М

Д

Решение:

Ж

К

1. для того, чтобы оставить только маршруты, проходящие через вершину В, нужно представить граф в таком виде, « собрав его в пучок » около вершины В :

В

А

М

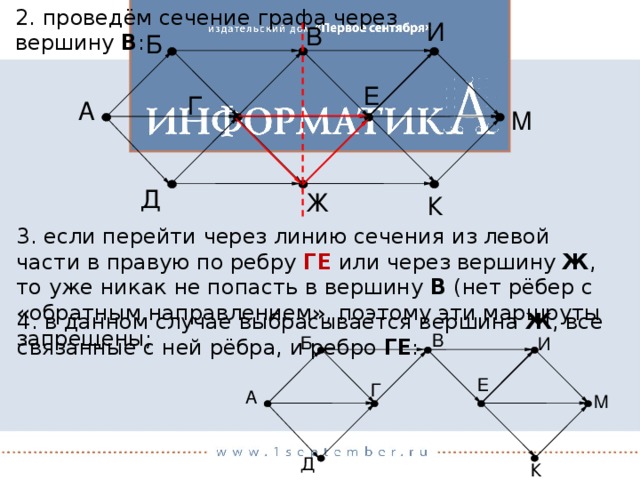
2. проведём сечение графа через вершину В :

И

B

Б

Е

Г

А

М

Д

Ж

К

3. если перейти через линию сечения из левой части в правую по ребру ГЕ или через вершину Ж , то уже никак не попасть в вершину В (нет рёбер с «обратным направлением», поэтому эти маршруты запрещены;

4. в данном случае выбрасывается вершина Ж , все связанные с ней рёбра, и ребро ГЕ :

B

Б

И

Е

Г

А

М

Д

К

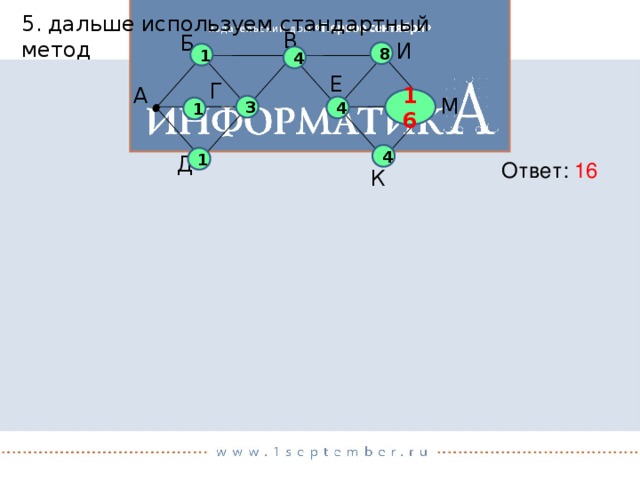
5. дальше используем стандартный метод

B

Б

И

8

1

4

Е

Г

А

16

М

3

4

1

4

1

Д

Ответ: 16

К

Пример III:

На карту нанесены 4 города (A, B, C и D). Известно, что

между городами A и С – три дороги

между городами C и B – две дороги

между городами A и B – две дороги

между городами C и D – две дороги

между городами B и D – четыре дороги

По каждой из этих дорог можно ехать в обе стороны. Сколькими различными способами можно проехать из города А в город D , посещая каждый город не более одного раза ?

Решение:

2

А

B

1. нарисуем граф, в котором множественные дороги из одного города в другой будем обозначать одной дугой и подписывать около неё количество дорог:

2

4

3

2. выпишем все маршруты, по которым можно ехать из A в D так, чтобы дважды не проезжать один и тот же город:

2

С

D

• 4

3 2

A  B  D

2 2 2

A  С  D

3 2 4

A  B  С  D

A  C  B  D

3. теперь рассмотрим маршрут A  B  D ;

2

А

B

• сначала можно двумя путями приехать из A в B

2

4

3

• затем – 4-мя путями из B в D

2

D

С

4. аналогично находим количество различных путей по другим маршрутам

A  С  D: 3*2 = 6

A  B  С  D: 2*2*2 = 8

A  C  B  D: 3*2*4 = 24

5. всего получается 8 + 6 + 8 + 24 = 46

Ответ: 46

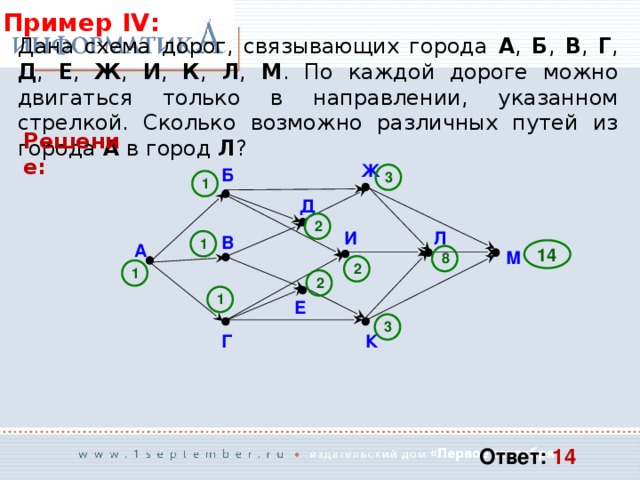
Пример IV:

Дана схема дорог, связывающих города А , Б , В , Г , Д , Е , Ж , И , К , Л , М . По каждой дороге можно двигаться только в направлении, указанном стрелкой. Сколько возможно различных путей из города А в город Л ?

Решение:

Ж

Б

3

1

Д

2

Л

И

В

1

А

14

М

8

2

1

2

1

Е

3

К

Г

Ответ: 14