Задание 5 (презентация по типам задач к ЕГЭ)

Ege 5

базовый уровень, 2 мин

Умение кодировать и декодировать информацию

Что нужно знать :

• кодирование может быть равномерное и неравномерное ; при равномерном кодировании все символы кодируются кодами равной длины; при неравномерном кодировании разные символы могут кодироваться кодами разной длины , это затрудняет декодирование

• закодированное сообщение можно однозначно декодировать с начала, если выполняется условие Фано : никакое кодовое слово не является началом другого кодового слова ;

• условие Фано – это достаточное, но не необходимое условие однозначного декодирования.

Пример I.

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А – 0; Б – 100; В – 1010; Г – 111; Д – 110. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны.

Каким из указанных способов это можно сделать?

1) для буквы В – 101 2) это невозможно

3) для буквы В – 010 4) для буквы Б – 10

Решение:

• вариант 3 не подходит, потому что новый код буквы В начинается с 0 (кода А), поэтому условие Фано нарушено

• вариант 4 не подходит, потому что код буквы В начинается с 10 (нового кода Б), поэтому условие Фано нарушено

Ответ: 1.

Пример II.

По каналу связи передаются сообщения, содержащие только 4 буквы:

А, И, С, Т. В любом сообщении больше всего букв А , следующая по частоте буква – С , затем – И . Буква Т встречается реже, чем любая другая. Для передачи сообщений нужно использовать неравномерный двоичный код, допускающий однозначное декодирование; при этом сообщения должны быть как можно короче. Шифровальщик может использовать один из перечисленных ниже кодов. Какой код ему следует выбрать?

• А – 0, И – 1, С – 00, Т – 11
• С – 1, И – 0, А – 01, Т – 10
• А – 1, И – 01, С – 001, Т – 000
• С – 0, И – 11, А – 101, Т – 100

Решение:

• сначала выберем коды, допускающие однозначное декодирование:

это коды 3 и 4 (для них выполняется условие Фано),

коды 1 и 2 не подходят

   А – 1, И – 01, С – 001, Т – 000 при кодировании кодом 3 получаем сообщение длиной L 3 =  + 3  + 2  +3  С – 0, И – 11, А – 101, Т – 100 при кодировании кодом 4 получаем сообщение длиной L 4 = 3  +  + 2  +3  находим разность: L 4 ­– L 3 = ( 3  +  +2  +3  ) – (  +3  +2  +3  ) = 2  – 2  поскольку   , получаем L 4 ­– L 3 0 , то есть код 3 более экономичный Ответ: 3 " width="640"

Далее, сравним коды 3 и 4 , предполагая, что в сообщении

буква А встречается  раз, буква С –  раз, буква И –  раз и буква Т –  раз;

причём по условию задачи    

• А – 1, И – 01, С – 001, Т – 000

при кодировании кодом 3 получаем сообщение длиной

L 3 =  + 3  + 2  +3 

• С – 0, И – 11, А – 101, Т – 100

при кодировании кодом 4 получаем сообщение длиной

L 4 = 3  +  + 2  +3 

находим разность: L 4 ­– L 3 = ( 3  +  +2  +3  ) – (  +3  +2  +3  ) = 2  – 2 

поскольку   , получаем L 4 ­– L 3 0 , то есть код 3 более экономичный

Ответ: 3

Пример III.

По каналу связи передаются сообщения, содержащие только 4 буквы: Е, Н, О, Т . Для кодирования букв Е, Н, О используются 5 -битовые кодовые слова: Е - 00000 , Н - 00111 , О - 11011 . Для этого набора кодовых слов выполнено такое свойство : любые два слова из набора отличаются не менее чем в трёх позициях . Это свойство важно для расшифровки сообщений при наличии помех. Какое из перечисленных ниже кодовых слов можно использовать для буквы Т , чтобы указанное свойство выполнялось для всех четырёх кодовых слов?

• 11111
• 11100
• 00011
• не подходит ни одно из указанных выше слов

Решение:

• код, рассмотренный в условии задачи, относится к помехоустойчивым кодам, которые позволяют обнаружить и исправить определенное количество ошибок, вызванных помехами при передаче данных;

• количество позиций , в которых отличаются два кодовых слова одинаковой длины, называется расстоянием Хэмминга

• код, в котором расстояние Хэмминга между каждой парой кодовых слов равно d , позволяет обнаружить до d -1 ошибок; для исправления r ошибок требуется выполнение условия

d ≥ 2r + 1, поэтому код с d = 3 позволяет обнаружить одну или две ошибки, и исправить одну ошибку.

• легко проверить, что для заданного кода ( Е - 00000, Н - 00111, О - 11011 ) расстояние Хэмминга равно 3 ; в таблице выделены отличающиеся биты, их по три в парах Е-Н и Н-О и четыре в паре Е-О :

• теперь проверяем расстояние между известными кодами и вариантами ответа; для первого ответа 11111 получаем минимальное расстояние 1 (в паре О-Т ), этот вариант не подходит :

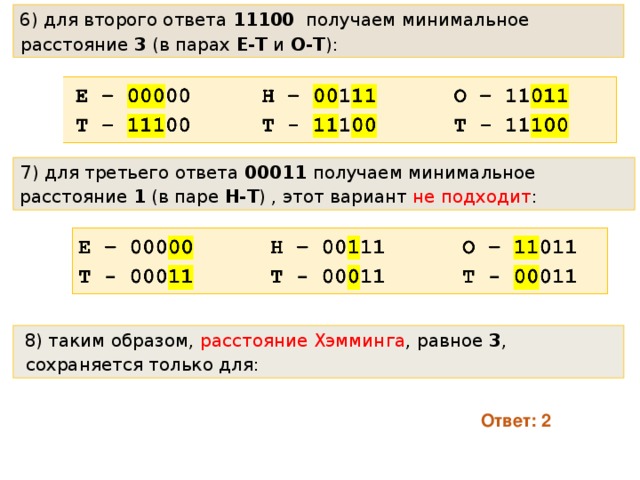
• для второго ответа 11100 получаем минимальное расстояние 3 (в парах Е-Т и О-Т ):

• для третьего ответа 00011 получаем минимальное расстояние 1 (в паре Н-Т ) , этот вариант не подходит :

• таким образом, расстояние Хэмминга , равное 3 , сохраняется только для:

Ответ: 2

Пример IV .

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А–00, Б–010, В–011, Г–101, Д–111 . Можно ли сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно ? Коды остальных букв меняться не должны. Выберите правильный вариант ответа.

• для буквы Б – 01 2) это невозможно

3) для буквы В – 01 4) для буквы Г – 01

Решение ( проверка условий Фано ) :

не подходит ;

Пример V.

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д , решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Использовали код: А–1, Б–000, В–001, Г–011 . Укажите, каким кодовым словом должна быть закодирована буква Д . Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования.

1) 00 2) 01 3) 11 4) 010

Пример VI.

Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11 , соответственно). Если таким способом закодировать последовательность символов БАВГ и записать результат шестнадцатеричным кодом, то получится

1) 4B 16 2) 411 16 3)BACD 16 4) 1023 16

0100 1011 2 =4B 16

Пример VII.

Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв – из двух бит , для некоторых – из трех ). Эти коды представлены в таблице:

A

B

000

C

01

D

100

E

10

011

Определить, какой набор букв закодирован двоичной строкой 0110100011000

1) EBCEA 2) BDDEA 3) BDCEA 4) EBAEA

Пример VIII.

Для передачи по каналу связи сообщения, состоящего только из букв А, Б, В, Г, решили использовать неравномерный по длине код: A=0, Б=10, В=110 . Как нужно закодировать букву Г , чтобы длина кода была минимальной и допускалось однозначное разбиение кодированного сообщения на буквы?

1) 1 2) 1110 3) 111 4) 11

По каналу связи передаются сообщения, содержащие только 4 буквы П , О , С , Т . Для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т , О , П используются такие кодовые слова: Т – 101, О – 0, П – 100 .

Укажите кратчайшее кодовое слово для буквы С , при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

Решение:

• код 0 – не годится (совпадает с кодом буквы О );

• код 1 – не годится (совпадает с началом кодов 100 и 101 );

• код 10 – не годится (совпадает с началом кодов 100 и 101 );

• код 11 – не совпадает с началом никакого из имеющихся кодов и ни с одним из имеющихся кодов.

Ответ: 11

Пример IX.

Черно-белое растровое изображение кодируется построчно, начиная с левого верхнего угла и заканчивая в правом нижнем углу. При кодировании 1 обозначает черный цвет, а 0 – белый .

Для компактности результат записали в шестнадцатеричной системе счисления. Выберите правильную запись кода.

1) BD 9 AA 5 2) BDA 9 B 5 3) BDA 9 D 5 4) DB 9 DAB

Решение

• «вытянем» растровое изображение в цепочку:

• черные ячейки заполним единицами , а белые – нулями :

1

1 строка

0

1

1

1

1

0

2 строка

1

1

0

1

0

1

3 строка

0

0

1

1

1

0

1

4 строка

0

1

0

1

• разобьем полоску на тетрады – группы из четырех ячеек

• получаем последовательно цепочку BDA9D5

Ответ: 3

Пример X.

Для передачи чисел по каналу с помехами используется код проверки четности . Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4 , и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23 , то получим последовательность 0010 1 0011 0 ). Определите, какое число передавалось по каналу в виде 01010100100111100011 ?

1) 59143 2) 5971 3) 102153 4) 10273

В примере:

2 = 0010 2 , бит четности (0 + 0 + 1 + 0) mod 2 = 1

3 = 0011 2 , бит четности (0 + 0 + 1 + 1) mod 2 = 0

• разобьём заданную последовательность на группы по 5 бит в каждой:

01010, 10010, 01111, 00011.

0101, 1001, 0111, 0001.

• отбросим пятый (последний) бит в каждой группе:

Демо - 2016

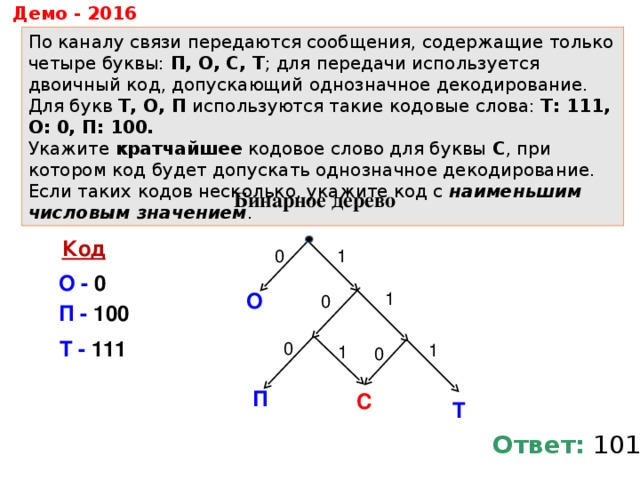
По каналу связи передаются сообщения, содержащие только четыре буквы: П, О, С, Т ; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, П используются такие кодовые слова: Т: 111, О: 0, П: 100.

Укажите кратчайшее кодовое слово для буквы С , при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением .

Бинарное дерево

Код

0

1

О - 0

О

1

0

П - 100

Т - 111

0

1

1

0

П

С

Т

Ответ: 101

ege5. 70. Для передачи помехоустойчивых сообщений в алфавите, который содержит 16 различных символов, используется равномерный двоичный код. Этот код удовлетворяет следующему свойству: в любом кодовом слове содержится четное количество единиц (возможно, ни одной ).

Какую наименьшую длину может иметь кодовое слово?

1. 5 2. 6 3. 3 4. 4

Решение.

Существует 16 двоичных слов длины 4. Т.к. среди них есть слова, содержащие 1 или 3 единицы, то в нашем коде нужно использовать кодовые слова с длиной больше, чем 4. Слов длины 5 достаточно. Искомые кодовые слова можно получать, например, добавляя к каждому из 16 возможных двоичных слов справа « бит четности », равный 0 , если 4 - значное двоичное слово содержит четное количество единиц , и равный 1 в противном случае. Например , двоичное слово 0000 преобразуется в 00000, а двоичное слово 1011 – в 10111.