5 – сабак
АЛГЕБРАЛЫК ТУЮНТМАЛАР.
Сандардын жана тамгалардын алгебралык амалдардын жардамында туюнтулуп жазылышы алгебралык туюнтма деп аталат.
ax3+bх2 – cх + n алгебралык туюнтма. Мында a,b,c – чыныгы сандар белгисиздин коэфиценттери , n – бош мүчө, x– өзгөрүлмө чоңдук.
Алгебралык туюнтмаларды жөнөкөйлөтүүдө кыскача көбөйтүүнүн формулалары, даражанын касиеттери жана арифметикалык амалдарды аткаруу тартиптери өз тартиби менен колдонулат.
Мисал маселелерди чыгарууда колдонула турган
формулалар жана негизги түшүнүктөр.
Көп мүчөлөрдөгү кыскача көбөйтүүнүн формулалары
(а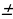 в)2 =а2
в)2 =а2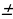 2ав + в2
2ав + в2
(a – b)2n = (b – a)2n
(a – b)2n+1 = - (b – a)2n+1
(a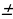 b+c)2 = a2 +b2 +c2 +2(
b+c)2 = a2 +b2 +c2 +2(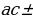 ab
ab 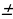 bc)
bc)
а2 – в2 = (а – в)(а + в)
а2 + в2 = (а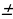 в)2
в)2 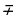 2ав
2ав
(а 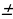 в)3 =а3
в)3 =а3 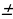 3а2в + 3ав2
3а2в + 3ав2 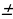 в3 =а3
в3 =а3 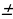 в3
в3 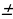 3ав(а
3ав(а 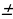 в)
в)
а3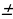 в3 = (а
в3 = (а 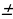 в)(а2
в)(а2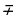 ав + в2)
ав + в2)
аn – bn = (a – b)(a n -1 + an-2b + an-3b2 + …+a2bn-3+abn-2+bn-1), n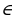 Z+
Z+
аn + bn =(a + b)(a n -1 - an-2b + an-3b2 - …+a2bn-3- abn-2+bn-1),n=2k+1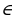 Z+
Z+
Катыштар жана пайыздар
Мейли 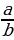 =
= 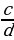 катышы берилсин, ал үчүн төмөндөгү барабардыктар аткарылат: ad = bc ,
катышы берилсин, ал үчүн төмөндөгү барабардыктар аткарылат: ad = bc , 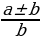 =
= 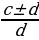 ,
, 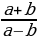 =
= 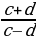 ,
,
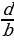 =
= 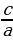 ,
, 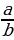 =
= 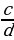 ,
, 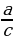 =
= 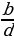 ,
, 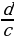 =
= 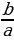 ,
, 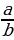 =
= 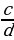 =
= 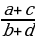 =
= 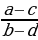 ,
, 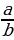 =
= 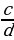 =
= 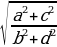 , a
, a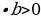
Эскертүү: 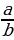 =
= 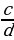 =
= 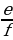
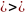 a:c:e = b:d:f болот.
a:c:e = b:d:f болот.
a жана b нын арифметикалык орто саны - 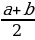 , ал эми геометриялык орто саны -
, ал эми геометриялык орто саны - 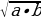 болот.
болот.
Төмөндөгү формула менен берилген эки өзгөрүлмөнүн көз карандылыгы түз пропорциялуулук деп аталат. y = kx .
Төмөндөгү формула менен берилген эки өзгөрүлмөнүн көз карандылыгы тескери пропорциялуулук деп аталат. y = 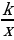 .
.
Берилген нерсенин жүздөн бир бөлүгү бир пайыз деп аталат.
Берилген нерсенин өлчөмүн А деп анын В % табуу керек болсо, анда:
В% = 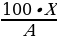 % , ал эми Х =
% , ал эми Х = 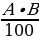 болот.
болот.
Даражалар менен болгон амалдар
a0 = 1 мында a ≠ 0, a ∈ R; 2) a− n = 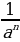 ;
;
3) an ∙ am = an+m; 4) 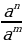 = an−m; 5) an∙bn = (a∙b)n;
= an−m; 5) an∙bn = (a∙b)n;
6) 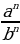 = (
= (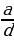 ) n , мында (b ≠ 0); 7)
) n , мында (b ≠ 0); 7) 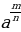 =
= 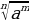 .
.
8) (abcd…)n = an bn cn dn … , 9) an bn cn dn … = (abcd…)n ,
10) (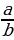 )n =
)n = 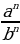 , 11_ (an)m = anm.
, 11_ (an)m = anm.
Тамырлар менен болгон амалдар
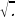 - тамырдын абсалюттук чоңдук белгиси.
- тамырдын абсалюттук чоңдук белгиси.
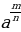 =
= 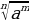 экендигин түшүндүрөт.
экендигин түшүндүрөт.
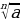 =
= 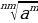 ,
, 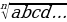 =
= 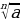
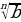
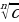
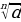 … ,
… ,
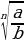 =
= 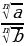 , (
, (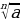 )m =
)m =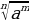 , (
, (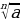 )n=a.
)n=a.
Чексиз тамырлар:
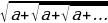 =
= 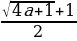
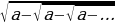 =
= 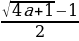
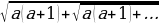 = a+1
= a+1
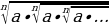 =
= 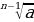
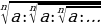 =
= 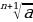
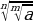 =
=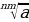 ,
, 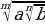 =
= 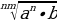 .
.
x = a +b, y = a b, a
b, a b
b 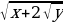 =
= 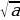 +
+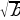
,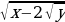 =
= 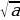
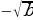 .
.
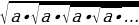 =
= 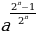 .
.
Арифметикалык прогрессия
Экинчи мүчөсүнөн баштап ар бир мүчөсү, өзүнөн мурда келүүчү мүчөсүнө бир эле санды кошуудан алынган сан удаалаштыгы, арифметикалык прогрессия деп аталат.
(an ) = a1 ,a2, ,a3, … , an , ...
Арифметикалык прогрессиянын ар кандай мүчөсү an = a1 + d(n – 1) формуласы менен эсептелип табылат.
Арифметикалык прогрессиянын биринчи жана акыркы мүчөсү белгилүү болсо, анын d айрымасын d = 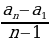 формуласы менен эсептейбиз.
формуласы менен эсептейбиз.
Арифметикалык прогрессиянын каалагандай эки мүчөсү белгилүү болсо анын d айрымасын
d = 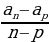 формуласы менен эсептейбиз.
формуласы менен эсептейбиз.
d = a2 –a1 = a3 – a2 = … = an – an-1 экендиги белгилүү.
an = 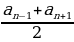
Арифметикалык прогрессиянын биринчи, акыркы мүчөсү жана айрымасы белгилүү болсо анын мүчөлөрүнүн санын
n = 1 + 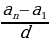 формуласы менен эсептейбиз.
формуласы менен эсептейбиз.
Арифметикалык прогрессиянын алгачкы n мүчөсүнүн суммасын
Sn = 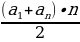 =
= 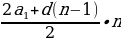 формуласы менен эсептейбиз.
формуласы менен эсептейбиз.
Геометриялык прогрессия
Экинчи мүчөсүнөн баштап ар бир мүчөсү, өзүнөн мурда келүүчү мүчөсүнө бир эле санды көбөйтүүдөн алынган сан удаалаштыгы геомертиялык прогрессия деп аталат.
(bn ) = b1 ,b2, ,b3, … , bn , ...
Геомертиялык прогрессиянын ар кандай мүчөсү bn = b1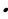 q n-1
q n-1
формуласы менен эсептелет.
q - геомертиялык прогрессиянын бөлүмү.
q = 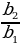 =
= 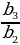 = … =
= … = 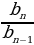 формуласы менен эсептейбиз.
формуласы менен эсептейбиз.
Геомертиялык прогрессиянын алгачкы n мүчөсүнүн суммасын
Sn = 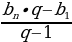 =
= 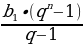 =
= 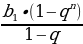 формуласы менен эсептейбиз. Чексиз кемүүчү геомертиялык прогрессиянын суммасын Sn =
формуласы менен эсептейбиз. Чексиз кемүүчү геомертиялык прогрессиянын суммасын Sn = 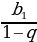 формуласы менен эсептейбиз.
формуласы менен эсептейбиз.
Кээ бир сан удаалаштыктарынын n мүчөлөрүнүн суммасынын формулалары
1 + 2 + 3 + 4 + 5 + ... + п = 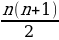 ;
;
2 + 4 + 6 + … + 2n = n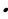 (n + 1);
(n + 1);
1 + 3 + 5 + … + (2n – 1) = n2
Логарифмалар
а негизи боюнча b санынын логарифмасы деп, b санынын алуу үчүн а санын даражага көтөрүүгө керек болгон с саны аталат.
logab = c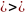 ac = b
ac = b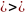 a logab = b, мында а
a logab = b, мында а 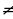 1 жана а
1 жана а  0
0
1. loga (b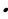 c)
c) = logab +
= logab + logaс 4. loge b =ln b 7. logaa = 1
logaс 4. loge b =ln b 7. logaa = 1
2. loga 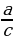 = logab -
= logab - logaс 5. logab =
logaс 5. logab =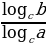 8. loga1 = 0
8. loga1 = 0
3. logabn = n logab 6. log10b = lgb 9. ln e = 1
10. logab =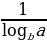 11. loga
11. loga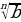 =
= 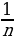 logab
logab
Белгисиз өзгөрүлмөсү логарифма белгисинин алдында турган теңдеме, логарифмалык теңдеме д.а.
loga f(x) = b түрүндөгү теңдеме эң жөнөкөй логарифмалык теңдеме болуп эсептелет.
loga f(x) = b 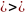 f(x) = ab теңдемеси менен тең күчтүү.(a 0,a
f(x) = ab теңдемеси менен тең күчтүү.(a 0,a 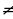 1, f(x)0 болуусу шарт).
1, f(x)0 болуусу шарт).
Логарифмалык теңдемелерди чыгаруудан мурда анын жашоо областын табып,, андан кийин теңдемени чыгарып, теңдеменин жашоо областын эске алуу менен жообун жазуу керек.
Логарифмалык теңдемелерди чыгарууда көбүнчө төмөнкү ыкмалар колдонулат.
Логарифманын аныктамасына негизделген теңдемелерди чыгаруу;
Потенцирлөөнүн жардамында чыгаруу; (барабардыктын эки жагын тең бирдей негизе келтирип логарифмаларда таштап жиберүү жолу)
Негизги логарифмалык теңдештиктерди колдонуу;
Логарифмалоону колдонуу;
Жаңы өзгөрмө киргизүү;
Жаңы негиз боюнча логарифмалоо.
Тригонометриялык негизги формулалар.
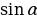 =
= 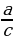 ,
, 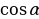 =
= 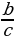 , tg
, tg 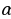 =
= 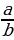 , ctg
, ctg 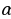 =
= 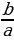
tg 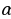 =
= 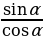
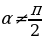 +
+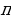 n , ctg
n , ctg 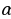 =
= 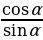
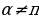 n .
n .
sin(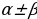 ) = sin
) = sin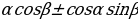
cos (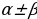 ) =
) = 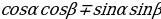 ушул төрт формулалардан калган формулалардын баары келип чыгат
ушул төрт формулалардан калган формулалардын баары келип чыгат



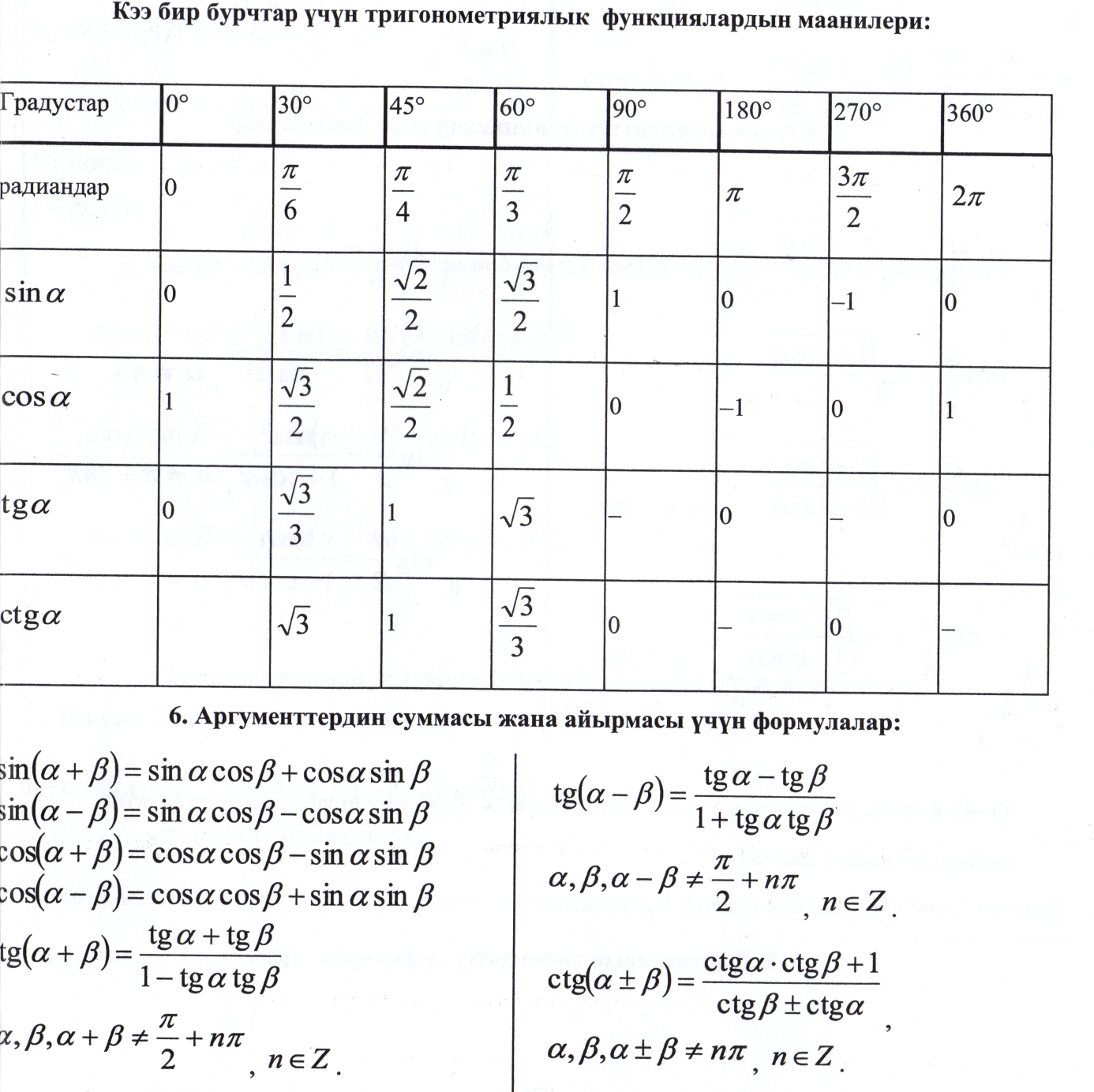




Мисалдар иштөө:
1.Туюнтманы жөнөкөйлөткүлө 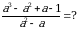 А)3 Б)4 В)5 Г)6 Д)7
А)3 Б)4 В)5 Г)6 Д)7
Жөнөкөйлөтүү:
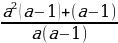 =
= 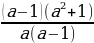 =
= 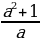 жообу (А)
жообу (А)
А) 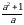 Б)
Б) 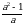 В)
В) 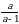 Г)
Г) 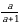 Д)
Д) 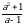
Эгерде 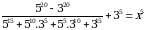 x ти тап ?
x ти тап ?
Мында кыскача көбөйтүүнүн формуласын жана көбөйтүүнүн кошууга карата топтоштуруу эрежесин пайдаланабыз.
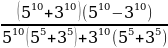

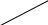 + 35 =
+ 35 = 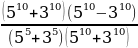 + 35 =
+ 35 = 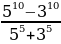 + 35 =
+ 35 =
= 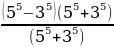 + 35 =
+ 35 = 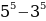 + 35 = 55 = х5 мындан х = 5 к.ч.
+ 35 = 55 = х5 мындан х = 5 к.ч.
жообу (В)
Туюнтманы жөнөкөйлөткүлө 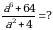
А) 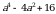 Б)
Б) 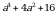 В)
В) 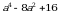 Г)
Г) 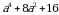 Д)
Д) 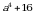
Эгерде 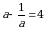 болсо, эсепте
болсо, эсепте 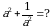
Биринчи барабардыктын эки жагын тең квадратка көтөрсөк :
(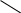 a
a 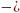
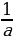 )2 = 42
)2 = 42 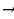 a2 – 2 a
a2 – 2 a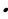
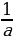 +
+ 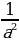 = 16
= 16 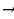 a2 – 2 +
a2 – 2 + 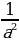 = 16
= 16 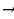 a2 +
a2 + 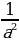 = 18
= 18
Жообу (А)
А)18 Б)16 В)14 Г)12 Д) 10
Эгерде 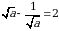 болсо, эсептегиле
болсо, эсептегиле 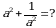
А) 4 Б) 6 В)18 Г) 34 Д) 36
Эгерде 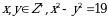 болсо, эсептегиле 2x – y = ?
болсо, эсептегиле 2x – y = ?
А)11 Б)13 В)17 Г) 21 Д) 30
Эгерде 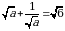 болсо, эсептегиле
болсо, эсептегиле 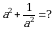
А)14 Б) 16 В) 20 Г)24 Д)36
Эгерде 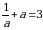 болсо, эсептегиле
болсо, эсептегиле 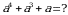
Эсептөө:
Биринчи туюнтмадан а2 жана а2 + 1 дин маанилерин табалы
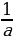 +a =3
+a =3 1+a2=3a жана а2 =3а – 1 болот. Бул маанилерди экинчи туюнтмага алып барып койсок анда:
1+a2=3a жана а2 =3а – 1 болот. Бул маанилерди экинчи туюнтмага алып барып койсок анда:
(a2)2 + a(a2 +1) = (3а – 1)2 + а .3а = 9а2 – 6а +1 + 3а2 =12а2 – 6а +1=
= 12(3а – 1) – 6а + 1= 36а – 12 – 6а + 1 = 30а – 11 . жообу (Г)
А) 8a - 7 Б) 14a – 9 В) 12a - 30 Г) 30a - 11 Д) 30a – 19
Эгерде 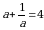 болсо, эсептегиле
болсо, эсептегиле 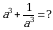
А) 42 Б) 48 В) 50 Г) 52 Д) 56
Эгерде a – b = 3, a b=8 болсо, тапкыла
b=8 болсо, тапкыла 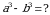
А) 72 Б) 88 В) 94 Г) 99 Д) 111
Эгерде 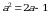 болсо,тапкыла
болсо,тапкыла 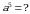
А) 2a - 1 Б) 5a – 4 В) -4a+3 Г) a - 18 Д) 7a – 3
Эгерде 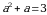 болсо, эсептегиле
болсо, эсептегиле 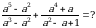
А)3 Б) 4 В) 6 Г) 7 Д) 10
Эсептегиле 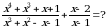
А) 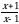 Б) x+1 В) x-1 Г) x Д) 1
Б) x+1 В) x-1 Г) x Д) 1
Эсептегиле 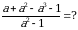
А) 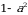 Б)
Б) 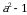 В) a+1 Г) a-1 Д) 1-a
В) a+1 Г) a-1 Д) 1-a
Эсептегиле 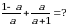
А) 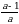 Б)
Б) 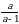 В)
В) 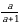 Г)
Г) 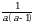 Д)
Д) 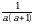
Эсептегиле 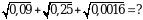
А) 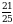 Б)
Б) 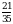 В)
В) 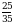 Г)
Г) 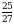 Д) 0
Д) 0
Эсептегиле 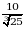 =?
=?
А) 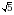 Б)
Б) 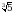 В)
В) 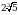 Г)
Г) 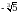 Д)
Д) 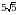
Эсептегиле 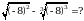
А) -16 Б) -8 В) 0 Г) 8 Д) 16
Эсептегиле 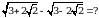
А) 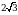 Б)
Б) 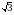 В)
В) 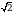 Г) 3 Д) 2
Г) 3 Д) 2
Эсептегиле 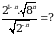 А)
А) 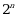 Б)
Б) 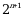 В)
В) 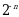 Г)
Г) 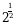 Д)
Д) 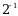
Эгерде 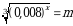 болсо,
болсо, 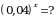 тапкыла.
тапкыла.
А) 2m Б) 3m В) 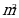 Г)
Г) 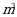 Д)
Д) 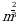
Эсептегиле 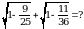
А) 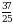 Б)
Б) 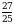 В)
В) 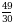 Г)
Г) 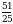 Д)
Д) 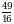
Эсептегиле 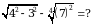 А) 0 Б) 1 В) 2 Г) 3 Д) 4
А) 0 Б) 1 В) 2 Г) 3 Д) 4
Эсептегиле 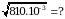 А) 0,3 Б) 0,9 В) 3 Г) 9 Д)
А) 0,3 Б) 0,9 В) 3 Г) 9 Д) 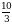
Эсептегиле 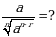
А) 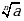 Б)
Б) 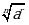 В)
В) 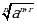 Г)
Г) 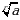 Д)
Д) 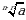
Эсептегиле 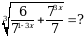
А) 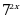 Б)
Б) 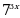 В)
В) 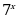 Г) 7 Д) 49
Г) 7 Д) 49
Эсептегиле 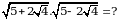 А) 2 Б) 3 В) 4 Г) 9 Д) 16
А) 2 Б) 3 В) 4 Г) 9 Д) 16
Эгерде 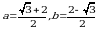 болсо,
болсо, 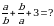 тапкыла
тапкыла
А) 12 Б) 15 В) 17 Г) 19 Д) 21
Эсептегиле 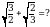
А) 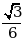 Б)
Б) 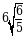 В)
В) 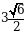 Г)
Г) 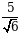 Д)
Д) 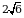
Эсептегиле 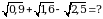
А)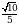 Б)1,2 В) 0,2 Г)
Б)1,2 В) 0,2 Г) 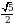 Д)
Д) 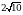
Эсептегиле 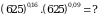
А)1 Б) 5 В) 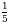 Г) 25 Д)
Г) 25 Д) 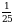
Эгерде 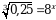 болсо, x ти тапкыла ?
болсо, x ти тапкыла ?
А) 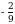 Б)
Б) 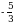 В)
В) 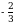 Г)
Г) 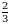 Д)
Д) 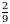
Эсептегиле 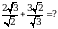
А) 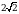 Б)
Б) 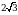 В)
В) 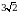 Г)
Г) 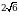 Д)
Д) 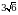
Эсептегиле 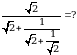 А)
А) 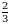 Б)
Б) 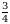 В)
В) 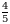 Г)
Г) 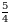 Д)
Д) 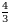
Эсептегиле 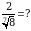 А)
А) 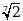 Б)
Б) 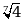 В)
В) 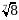 Г)
Г) 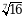 Д)
Д) 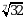
24. Амалдарды аткаргыла:
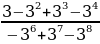
а) 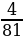 б)
б) 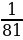 в) -
в) - 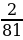 г)
г) 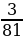 д)
д) 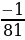
25.Амалдарды аткаргыла:
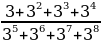
а) 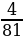 б)
б) 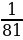 в) -
в) - 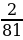 г)
г) 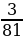 д)
д) 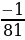
26.Амалдарды аткаргыла:
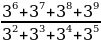
а) 81, б) 88, в) 87, г)12, д) 7
27.Амалдарды аткаргыла:
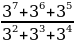
а) 81, б) 28, в) 27, г)12, д) 9
28.Амалдарды аткаргыла:
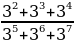
а) 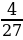 б)
б) 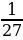 в) -
в) - 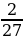 г)
г) 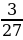 д)
д) 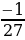
29.Амалдарды аткаргыла:
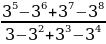
а) 81, б) 88, в) -81, г)12, д) 27
30.Амалдарды аткаргыла: 3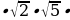 4
4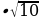
а) 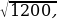 б) 3
б) 3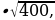 в) 4
в) 4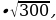 г) 120, д) 1200.
г) 120, д) 1200.
Базарда алманын баасы 20% га жогорулап, андан 10% га арзандаса баа канча пайызга өзгөргөн?
а) 8% га өстү, б) 4% га өстү, в) 10% га өстү, г) 2% га төмөндөдү,
д)10% га төмөндөдү.
Базарда нандын баасы 10% га жогорулап, андан 20% га арзандаса баа канча пайызга өзгөргөн?
а) 8% га өстү, б) 14% га өстү, в) 10% га өстү, г) 12% га төмөндөдү,
д)10% га төмөндөдү.
33. 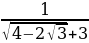 туюнтмасын жөнөкөйөт.
туюнтмасын жөнөкөйөт.
а) 1 - 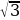 , б)
, б)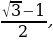 в)
в) 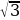 + 1, г)
+ 1, г) 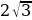 -1, д) 2 -
-1, д) 2 - 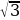 .
.
34. 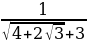 туюнтмасын жөнөкөйөт.
туюнтмасын жөнөкөйөт.
а) 1 - 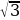 , б)
, б)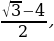 в)
в) 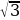 + 4, г)
+ 4, г) 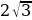 -1, д) 4 -
-1, д) 4 - 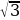 .
.
35. 7х2 – 17х + 10 = 0 теңдемсинин чоң тамырын тап?
а) - 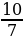 , б) -1, в) 1, г)
, б) -1, в) 1, г) 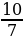 , д)
, д) 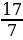 .
.
36. 7х2 +17х + 10 = 0 теңдемсинин кичине тамырын тап?
а) - 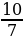 , б) -1, в) 1, г)
, б) -1, в) 1, г) 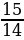 , д)
, д) 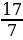 .
.
37.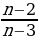 бөлчөгү бүтүн сан боло тургандай бардык п дердин бүтүн маанилеринин суммасын тап?
бөлчөгү бүтүн сан боло тургандай бардык п дердин бүтүн маанилеринин суммасын тап?
а) 1, б) -4, в) 3, г) -2, д) 6
38. 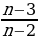 бөлчөгү бүтүн сан боло тургандай бардык п дердин бүтүн маанилеринин суммасын тап?
бөлчөгү бүтүн сан боло тургандай бардык п дердин бүтүн маанилеринин суммасын тап?
а) 1, б) 4, в) 3, г) -2, д) -4
39. Эгерде 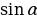 = 0,6 болсо (
= 0,6 болсо ( 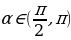 ,
, 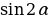 нин мааниси эмнеге барабар?
нин мааниси эмнеге барабар?
а) - 0,48, б) 0.48, в) – 0,96, г) 0,96, д) 0,24
40.Эгерде 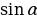 = 0,6 болсо (
= 0,6 болсо ( 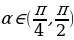 ,
, 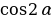 нин мааниси эмнеге барабар?
нин мааниси эмнеге барабар?
а) - 0,28, б) 0.28, в) – 0,16, г) 0,16, д) 0,24
41. Эгерде 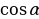 = -0,6 болсо (
= -0,6 болсо ( 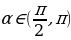 ,
, 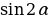 нин мааниси эмнеге барабар?
нин мааниси эмнеге барабар?
а) - 0,48, б) 0.48, в) – 0,96, г) 0,96, д) 0,24
42.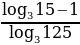 туюнтмасынын маанисин тап ?
туюнтмасынын маанисин тап ?
а) 2, б) 3, в) 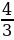 , г)
, г) 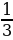 , д)
, д) 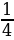 .
.
43.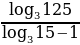 туюнтмасынын маанисин тап ?
туюнтмасынын маанисин тап ?
а) 2, б) 3, в) 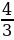 , г)
, г) 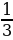 , д)
, д) 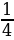 .
.
44. 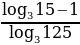 туюнтмасынын маанисин тап ?
туюнтмасынын маанисин тап ?
а) 2, б) 3, в) 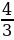 , г)
, г) 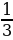 , д)
, д) 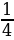 .
.
45. 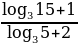 туюнтмасынын маанисин тап ?
туюнтмасынын маанисин тап ?
а) 1, б) 2, в) 3, г) 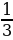 , д)
, д) 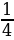 .
.
5 – сабак үчүн тапшырма
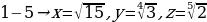
x
y
1
y
z
.
2
z
x
.
3
5x2
y8
.

4
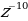
Х -10
.
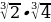
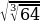
5.
6.
7
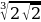
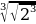
.
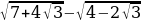
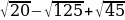
8.
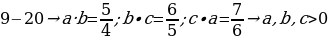
a
0
9
b
0
.
1
c
0
0.
1
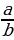
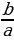
1.
1
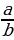
2.
1
b
- 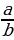
3
. 1
-a
4.
1
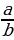
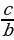
5.
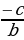
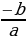
16.
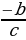
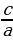
1

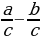
7. 18.
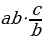
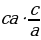
19.
2
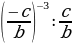
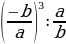
0.
21. х = a2b3 жана y = ab21 төрт орундуу сандар. Эгерде х – у = 2 болсо, b нын маанисин тап ?
1 B) 2 C) 3 D) 4 E) 5
22. a жана b – терс бүтүн сандар, жана 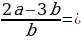 7 а + b сумма-сынын эң чоң маанисин тап ?
7 а + b сумма-сынын эң чоң маанисин тап ?
0 B) – 4 C) – 5 D) – 6 E) – 20
a,b,c – натуралдык сандар.Эгерде а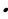 b=30 жана b
b=30 жана b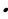 с=24 болсо,
с=24 болсо,
а + b + с нын эң кичине маанисин тап ?
15 B) 21 C) 29 D) 55 E) 61
34 жана 51 сандарынын, ЭЧЖБ 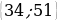 жана ЭКЖБ
жана ЭКЖБ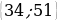 тап ?
тап ?
17 жана 51 B) 34 жана 102 C) 17 жана 102 D) 34 жана 51
E) 51 жана 1
25. 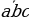 – саны 9 га бөлүнсө жана бирдиги 3 кө барабар болсо, цифралары (a
– саны 9 га бөлүнсө жана бирдиги 3 кө барабар болсо, цифралары (a b
b c) шартын канааттандыруучу канча үч орундуу сандар бар.
c) шартын канааттандыруучу канча үч орундуу сандар бар.
А) бир B) эки C) үч D) төрт E) беш
26. 5 ке бөлгөндө 3 калдык калуучу натуралдык сандын формуласы кайсы?
A)3n+5 B) 5 C) 3n-5 D) 5n+3 E) 3
27. 95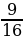 – 88
– 88 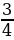 +
+ 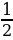
 0,0001: 0,005
0,0001: 0,005
А) 369 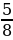 B) 365
B) 365 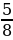 C) – 364 D) 366
C) – 364 D) 366 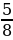 E) –365
E) –365 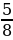
28. 500 санынын канча оң бүтүн бөлүүчүсү бар ?
A) 11 B) 12 C) 13 D) 10 E) 9
500х саны эмнеге барабар, эгерде 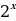 = n жана
= n жана 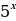 = m болсо, төмөнкүлөрдүн кимиси туура ?
= m болсо, төмөнкүлөрдүн кимиси туура ?
А) n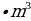 B)
B) 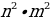 C)
C) 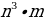 D)
D) 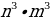 E)
E) 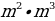
30. 2+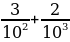 = ?
= ?
А) 2,32 B) 2,032 C) 2,303 D) 2,0032 E) 2,0302
31. а = 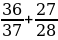 жана b =
жана b = 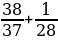 болсо, а ны b аркылуу туюнт.
болсо, а ны b аркылуу туюнт.
А) 1- b B) 2-b C) 3- b D) 1-3 b E) 3-2b
32. (1+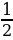 )
) (1+
(1+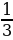 )
) (1+
(1+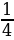 )
) ...
... (1+
(1+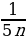 )=63
)=63
А) 20 B) 22 C) 24 D) 25 E) 29







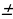 в)2 =а2
в)2 =а2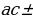 ab
ab 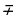 2ав
2ав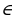 Z+
Z+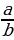 =
= 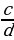 катышы берилсин, ал үчүн төмөндөгү барабардыктар аткарылат: ad = bc ,
катышы берилсин, ал үчүн төмөндөгү барабардыктар аткарылат: ad = bc , 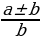 =
= 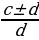 ,
, 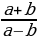 =
= 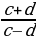 ,
,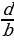 =
= 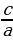 ,
, 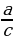 =
= 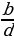 ,
, 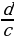 =
= 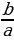 ,
, 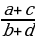 =
= 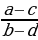 ,
, 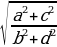 , a
, a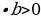
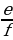
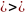 a:c:e = b:d:f болот.
a:c:e = b:d:f болот.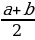 , ал эми геометриялык орто саны -
, ал эми геометриялык орто саны - 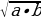 болот.
болот.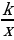 .
.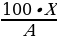 % , ал эми Х =
% , ал эми Х = 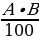 болот.
болот.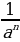 ;
;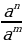 = an−m; 5) an∙bn = (a∙b)n;
= an−m; 5) an∙bn = (a∙b)n;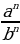 = (
= (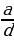 ) n , мында (b ≠ 0); 7)
) n , мында (b ≠ 0); 7) 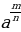 =
= 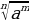 .
.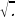 - тамырдын абсалюттук чоңдук белгиси.
- тамырдын абсалюттук чоңдук белгиси.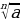 =
= 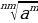 ,
, 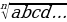 =
= 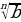
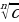
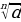 … ,
… ,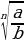 =
= 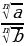 , (
, (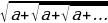 =
= 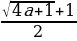
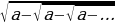 =
= 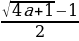
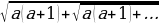 = a+1
= a+1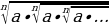 =
= 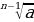
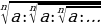 =
= 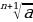
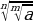 =
=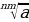 ,
, 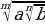 =
= 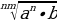 .
. b, a
b, a b
b 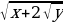 =
= 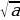 +
+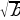
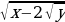 =
= 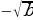 .
.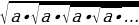 =
= 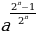 .
.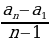 формуласы менен эсептейбиз.
формуласы менен эсептейбиз.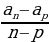 формуласы менен эсептейбиз.
формуласы менен эсептейбиз.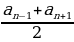
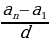 формуласы менен эсептейбиз.
формуласы менен эсептейбиз.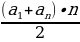 =
= 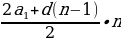 формуласы менен эсептейбиз.
формуласы менен эсептейбиз.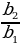 =
= 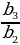 = … =
= … = 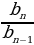 формуласы менен эсептейбиз.
формуласы менен эсептейбиз.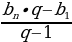 =
= 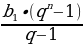 =
= 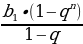 формуласы менен эсептейбиз. Чексиз кемүүчү геомертиялык прогрессиянын суммасын Sn =
формуласы менен эсептейбиз. Чексиз кемүүчү геомертиялык прогрессиянын суммасын Sn = 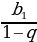 формуласы менен эсептейбиз.
формуласы менен эсептейбиз.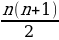 ;
; 1 жана а
1 жана а  = logab +
= logab +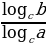 8. loga1 = 0
8. loga1 = 0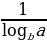 11. loga
11. loga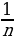 logab
logab 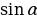 =
= 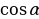 =
= 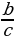 , tg
, tg 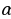 =
= 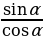
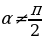 +
+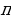 n , ctg
n , ctg 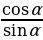
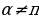 n .
n .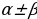 ) = sin
) = sin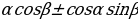
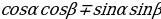 ушул төрт формулалардан калган формулалардын баары келип чыгат
ушул төрт формулалардан калган формулалардын баары келип чыгат








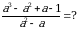 А)3 Б)4 В)5 Г)6 Д)7
А)3 Б)4 В)5 Г)6 Д)7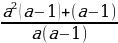 =
= 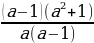 =
= 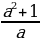 жообу (А)
жообу (А) 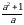 Б)
Б) 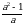 В)
В) 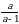 Г)
Г) 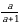 Д)
Д) 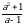
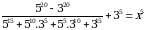 x ти тап ?
x ти тап ?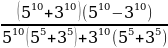

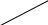 + 35 =
+ 35 = 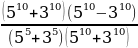 + 35 =
+ 35 = 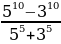 + 35 =
+ 35 = 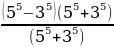 + 35 =
+ 35 = 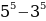 + 35 = 55 = х5 мындан х = 5 к.ч.
+ 35 = 55 = х5 мындан х = 5 к.ч. 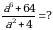
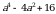 Б)
Б) 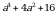 В)
В) 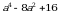 Г)
Г) 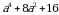 Д)
Д) 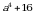
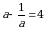 болсо, эсепте
болсо, эсепте 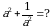
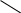 a
a 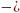
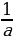 )2 = 42
)2 = 42 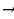 a2 – 2 a
a2 – 2 a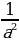 = 16
= 16 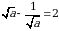 болсо, эсептегиле
болсо, эсептегиле 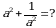
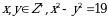 болсо, эсептегиле 2x – y = ?
болсо, эсептегиле 2x – y = ?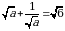 болсо, эсептегиле
болсо, эсептегиле 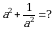
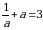 болсо, эсептегиле
болсо, эсептегиле 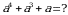
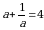 болсо, эсептегиле
болсо, эсептегиле 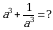
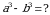
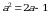 болсо,тапкыла
болсо,тапкыла 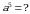
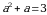 болсо, эсептегиле
болсо, эсептегиле 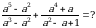
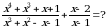
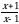 Б) x+1 В) x-1 Г) x Д) 1
Б) x+1 В) x-1 Г) x Д) 1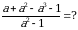
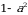 Б)
Б) 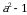 В) a+1 Г) a-1 Д) 1-a
В) a+1 Г) a-1 Д) 1-a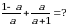
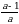 Б)
Б) 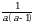 Д)
Д) 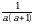
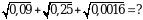
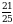 Б)
Б) 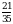 В)
В) 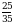 Г)
Г) 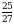 Д) 0
Д) 0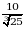 =?
=?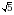 Б)
Б) 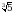 В)
В) 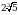 Г)
Г) 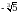 Д)
Д) 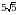
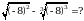
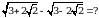
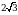 Б)
Б) 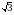 В)
В) 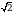 Г) 3 Д) 2
Г) 3 Д) 2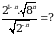 А)
А) 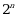 Б)
Б) 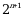 В)
В) 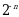 Г)
Г) 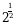 Д)
Д) 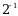
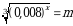 болсо,
болсо, 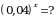 тапкыла.
тапкыла.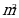 Г)
Г) 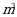 Д)
Д) 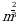
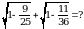
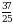 Б)
Б) 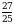 В)
В) 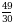 Г)
Г) 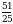 Д)
Д) 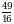
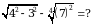 А) 0 Б) 1 В) 2 Г) 3 Д) 4
А) 0 Б) 1 В) 2 Г) 3 Д) 4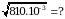 А) 0,3 Б) 0,9 В) 3 Г) 9 Д)
А) 0,3 Б) 0,9 В) 3 Г) 9 Д) 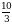
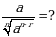
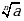 Б)
Б) 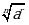 В)
В) 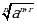 Г)
Г) 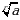 Д)
Д) 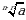
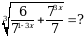
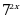 Б)
Б) 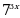 В)
В) 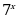 Г) 7 Д) 49
Г) 7 Д) 49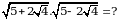 А) 2 Б) 3 В) 4 Г) 9 Д) 16
А) 2 Б) 3 В) 4 Г) 9 Д) 16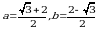 болсо,
болсо, 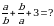 тапкыла
тапкыла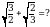
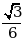 Б)
Б) 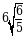 В)
В) 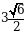 Г)
Г) 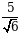 Д)
Д) 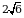
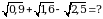
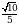 Б)1,2 В) 0,2 Г)
Б)1,2 В) 0,2 Г) 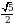 Д)
Д) 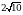
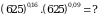
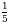 Г) 25 Д)
Г) 25 Д) 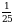
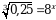 болсо, x ти тапкыла ?
болсо, x ти тапкыла ?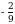 Б)
Б) 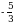 В)
В) 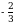 Г)
Г) 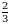 Д)
Д) 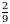
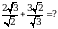
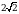 Б)
Б) 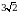 Г)
Г) 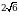 Д)
Д) 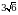
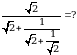 А)
А) 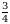 В)
В) 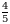 Г)
Г) 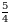 Д)
Д) 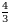
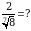 А)
А) 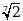 Б)
Б) 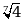 В)
В) 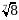 Г)
Г) 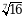 Д)
Д) 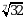
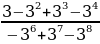
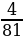 б)
б) 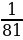 в) -
в) - 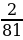 г)
г) 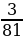 д)
д) 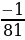
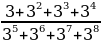
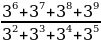
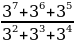
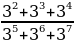
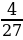 б)
б) 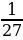 в) -
в) - 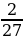 г)
г) 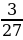 д)
д) 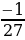
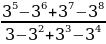
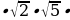 4
4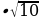
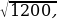 б) 3
б) 3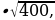 в) 4
в) 4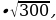 г) 120, д) 1200.
г) 120, д) 1200.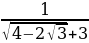 туюнтмасын жөнөкөйөт.
туюнтмасын жөнөкөйөт.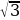 , б)
, б)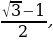 в)
в) 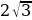 -1, д) 2 -
-1, д) 2 - 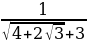 туюнтмасын жөнөкөйөт.
туюнтмасын жөнөкөйөт.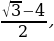 в)
в) 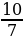 , б) -1, в) 1, г)
, б) -1, в) 1, г) 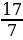 .
.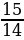 , д)
, д) 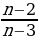 бөлчөгү бүтүн сан боло тургандай бардык п дердин бүтүн маанилеринин суммасын тап?
бөлчөгү бүтүн сан боло тургандай бардык п дердин бүтүн маанилеринин суммасын тап?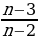 бөлчөгү бүтүн сан боло тургандай бардык п дердин бүтүн маанилеринин суммасын тап?
бөлчөгү бүтүн сан боло тургандай бардык п дердин бүтүн маанилеринин суммасын тап?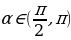 ,
, 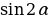 нин мааниси эмнеге барабар?
нин мааниси эмнеге барабар?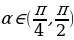 ,
, 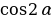 нин мааниси эмнеге барабар?
нин мааниси эмнеге барабар?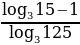 туюнтмасынын маанисин тап ?
туюнтмасынын маанисин тап ?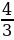 , г)
, г) 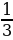 , д)
, д) 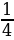 .
.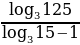 туюнтмасынын маанисин тап ?
туюнтмасынын маанисин тап ?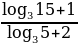 туюнтмасынын маанисин тап ?
туюнтмасынын маанисин тап ?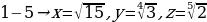
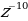
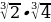
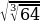
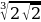
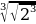
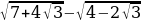
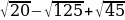
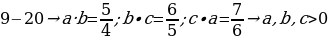
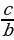
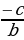
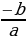
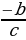

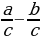
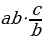
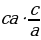
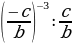
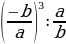
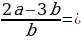 7 а + b сумма-сынын эң чоң маанисин тап ?
7 а + b сумма-сынын эң чоң маанисин тап ?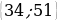 жана ЭКЖБ
жана ЭКЖБ – саны 9 га бөлүнсө жана бирдиги 3 кө барабар болсо, цифралары (a
– саны 9 га бөлүнсө жана бирдиги 3 кө барабар болсо, цифралары (a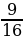 – 88
– 88 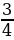 +
+ 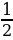
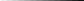 0,0001: 0,005
0,0001: 0,005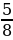 B) 365
B) 365 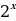 = n жана
= n жана 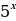 = m болсо, төмөнкүлөрдүн кимиси туура ?
= m болсо, төмөнкүлөрдүн кимиси туура ?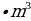 B)
B) 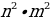 C)
C) 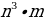 D)
D) 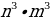 E)
E) 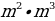
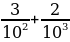 = ?
= ?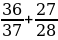 жана b =
жана b = 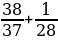 болсо, а ны b аркылуу туюнт.
болсо, а ны b аркылуу туюнт.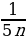 )=63
)=63









