Значение логического выражения (ОГЭ, задание 2)
Справочная информация
 Для максимально быстрого и однозначно верного решения задач будем придерживаться принципа: чем меньше вычислений и другой работы мы делаем, тем меньше вероятность появления ошибок в результате.
Для максимально быстрого и однозначно верного решения задач будем придерживаться принципа: чем меньше вычислений и другой работы мы делаем, тем меньше вероятность появления ошибок в результате.
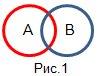
Для более наглядного отображения логических отношений между множествами точек А и В будем использовать геометрическую схему в виде кругов Эйлера.
Точка принадлежит множеству А, если она находится внутри круга, его ограничивающего, что записывается в виде А=1 (истина), иначе А=0 (ложь).
Правил при получении результатов выполнения логических операций много, а исключения всего два, поэтому и будем решать задачи при их использовании.
Результатом применения логических операций могут быть только истина (1) или ложь (0).
Существуют всего три базовые логические операции, при помощи которых строятся логические выражения: НЕ, И и ИЛИ.
НЕ: отрицание (инверсия). Обозначается знаком ¬ ,например, ¬А). Результат применения: ¬1 = 0, ¬0 = 1 , т.е. истина превращается в ложь, а ложь – в истину. Будем говорить, что операция НЕ (¬) переворачивает результат (значение).
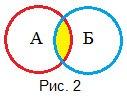 И: конъюнкция (логическое умножение) . Обозначается знаками /\ либо &, (например, А /\ В либо А & В). Результатом выполнения конъюнкции служит пересечение множеств А и В (на рис.2 выделено желтым цветом). При этом точка принадлежит пересечению множеств А и В, если она принадлежит одновременно обоим множествам:
И: конъюнкция (логическое умножение) . Обозначается знаками /\ либо &, (например, А /\ В либо А & В). Результатом выполнения конъюнкции служит пересечение множеств А и В (на рис.2 выделено желтым цветом). При этом точка принадлежит пересечению множеств А и В, если она принадлежит одновременно обоим множествам:
А & B = 1 при А=1 и В=1.
Во всех остальных случаях в результате применения выражения И получаем ложь. Т.о,. исключение № 1:
«И» правда, когда все части выражения правда.
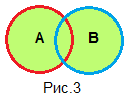
ИЛИ: дизъюнкция (логическое сложение). Обозначается \/ (например, А \/ В). Результатом выполнения конъюнкции служит объединение множеств А и В (на рис.3 выделено зеленым цветом). При этом точка не принадлежит объединению множеств А и В, если она не принадлежит ни А, ни В:
А \/ B = 0 при А=0 и В=0.
Во всех остальных случаях в результате применения выражения ИЛИ получаем правду.
 Т.о., исключение № 2:
Т.о., исключение № 2:
«ИЛИ» ложно, когда все части выражения ложны.
При вычислении логических выражений следует помнить, что логические операции выполняются в следующем порядке: НЕ, И, ИЛИ. Как и в математике, скобки могут поменять последовательность их выполнения.
При этом любая операция, которая выполняется последней, может поменять результат, а операция НЕ, стоящая перед скобками, переворачивает результат, полученный в скобках.
Применяя все выше сказанное, будем вычислять значение логического выражения от последней операции к первой, используя только два исключения и не открывая скобки.
Рассмотрим решение задач на примерах.
Задача 1.
Для какого из приведённых значений числа X ложно высказывание:
НЕ (X ИЛИ (X
1) 6
2) 5
3) 4
4) 3
Решение.
Последней операцией при вычислении этого выражения будет ИЛИ, а для нее действует исключение № 2.
 Следовательно,
Следовательно,
 НЕ (X ) ИЛИ (X 0
НЕ (X ) ИЛИ (X 0
0 ИЛИ 0 = 0
В левой части выражения тоже два действия. Разложим и их по порядку. Последней здесь выполняется операция НЕ, которая переворачивает результат выполнения действия в скобках. Тогда
 НЕ (X = 0
НЕ (X = 0
при НЕ ( 1 ) = 0
Отсюда следует, что выражение в левой скобке соответствует истине, а в правой – лжи (соответственно, при открытии скобок переворачиваем математический знак на противоположный, не забывая и про знак «=»), т.е.
4 ≤ Х
Таким образом, правильный ответ указан под номером 3.
Ответ: 3
Задача 2.
Для какого из приведённых значений числа X истинно высказывание:
НЕ (X И (X
1) 5
2) 6
3) 7
4) 8
Решение.
Последней операцией при вычислении этого выражения будет И, а для нее действует исключение № 1.

 Следовательно,
Следовательно,
НЕ (X ) И (X 1
1 И 1 = 1
В левой части выражения тоже два действия, разложим и их по порядку. Последней здесь выполняется операция НЕ, которая переворачивает результат выполнения действия в скобках.
 Тогда НЕ (X = 1
Тогда НЕ (X = 1
при НЕ ( 0 ) = 1
Отсюда следует, что выражение в левой скобке соответствует лжи (соответственно, при открытии скобок переворачиваем математический знак на противоположный, не забывая и про знак «=»), а в правой – истине т.е.
7 ≤ Х
Таким образом, правильный ответ указан под номером 4.
Ответ: 4
Задача 3.
Для какого из приведённых имён ложно высказывание:
НЕ ((Первая буква гласная) И (Последняя буква согласная))?
1) Вера
2) Степан
3) Анна
4) Иван
Решение.
Запишем задание в виде схемы:
НЕ ((Первая буква гласная) И (Последняя буква согласная)) = 0
НЕ ( И = 1 ) = 0
Последней в этом выражении будет выполняться операция НЕ, тогда для получения лжи в результате ее выполнения в общих скобках должна быть истина.
Поэтому применим для решения выражения во внутренних скобках исключение № 1:
(Первая буква гласная) И (Последняя буква согласная) = 1
когда обе части выражения истинны, т.е. первая буква имени – гласная, а последняя согласная, что соответствует имени Иван.
Ответ: 4
Задача 4.
Для какого из приведённых чисел ложно высказывание:
(число ИЛИ НЕ (число чётное) ?
1) 137
2) 64
3) 9
4) 8
Решение.

 Последней в этом выражении выполняется операция ИЛИ, тогда применяем исключение № 2.
Последней в этом выражении выполняется операция ИЛИ, тогда применяем исключение № 2.
Тогда (число ИЛИ НЕ (число чётное) = 0
0 ИЛИ НЕ ( 1 ) = 0
При открытии скобок в левой части выражения меняем знак переворачивает результат при ее открытии, т.е. в правой скобке записана истина.
Таким образом, получаем (число ≥ 40) ИЛИ (число четное), что соответствует числу 64.
Ответ: 2
Задача 5.
Для какой из приведённых последовательностей цветных бусин истинно высказывание:
(Вторая бусина жёлтая) И НЕ(Четвёртая бусина зелёная) И НЕ(Последняя бусина красная)
(К — красный, Ж — жёлтый, С — синий, З — зелёный) ?
1) СЗККЖК
2) ЖЖКСЗК
3) СЖСЗКЗ
4) КЖЗСКС
Решение.
Прежде всего, отметим, что данное выражение составлено из трех последовательных операций И, тогда, согласно исключению № 1, истина будет результатом выражения только в случае истинных результатов во всех трех частях выражения. Т.к. перед второй и третьей скобками стоит НЕ, то в выражение в этих скобках должно дать в ответе ложь, а в первой скобке – истину, то получаем выражение
(Вторая бусина жёлтая) И (Четвёртая бусина НЕ зелёная) И (Последняя бусина НЕ красная) = 1
Проверяем поочередно варианты ответа по частям данного выражения и вычеркиваем ложные:
Вторая бусина жёлтая: 1) СЗККЖК
2) ЖЖКСЗК
3) СЖСЗКЗ
4) КЖЗСКС
Четвёртая бусина НЕ зелёная: 1) СЗККЖК
2) ЖЖКСЗК
3) СЖСЗКЗ
4) КЖЗСКС
Последняя бусина НЕ красная: 1) СЗККЖК
2) ЖЖКСЗК
3) СЖСЗКЗ
4) КЖЗСКС
находим, что истинным ответом здесь будет вариант 4.
Ответ: 4
Задача 7.
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
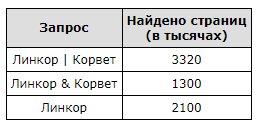
Сколько страниц в тысячах будет найдено по запросу Корвет ?
Решение:
Применив формулу ИЛИ = А + В - И, получаем:
3320 = 2100 + Корвет - 1300
Тогда Корвет = 3320 - 2100 + 1300 = 2520
Ответ: 2520
Задача 8.
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
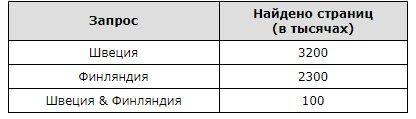
Сколько страниц (в тысячах) будет найдено по запросу Швеция | Финляндия ?
Решение:
Применив формулу ИЛИ = А + В - И, получаем:
Швеция | Финляндия = 3200 + 2300 - 100 = 5400
Ответ: 5400







 Для максимально быстрого и однозначно верного решения задач будем придерживаться принципа: чем меньше вычислений и другой работы мы делаем, тем меньше вероятность появления ошибок в результате.
Для максимально быстрого и однозначно верного решения задач будем придерживаться принципа: чем меньше вычислений и другой работы мы делаем, тем меньше вероятность появления ошибок в результате. И: конъюнкция (логическое умножение) . Обозначается знаками /\ либо &, (например, А /\ В либо А & В). Результатом выполнения конъюнкции служит пересечение множеств А и В (на рис.2 выделено желтым цветом). При этом точка принадлежит пересечению множеств А и В, если она принадлежит одновременно обоим множествам:
И: конъюнкция (логическое умножение) . Обозначается знаками /\ либо &, (например, А /\ В либо А & В). Результатом выполнения конъюнкции служит пересечение множеств А и В (на рис.2 выделено желтым цветом). При этом точка принадлежит пересечению множеств А и В, если она принадлежит одновременно обоим множествам: Т.о., исключение № 2:
Т.о., исключение № 2: Следовательно,
Следовательно,  НЕ (X ) ИЛИ (X 0
НЕ (X ) ИЛИ (X 0  Следовательно,
Следовательно, 

 Последней в этом выражении выполняется операция ИЛИ, тогда применяем исключение № 2.
Последней в этом выражении выполняется операция ИЛИ, тогда применяем исключение № 2.











