Значения синуса, косинуса, тангенса и котангенса углов.

Оценка: определяют результаты своей работы на уроке

Синтез: используют значения тригонометрических функций в решении задач

Анализ: изучают значения тригонометрических функций, работают с таблицей

Применение: демонстрируют применение значения синуса, косинуса, тангенса и котангенса произвольного угла

Понимание: обсуждают значения синуса, косинуса, тангенса и котангенса произвольного угла

Знание: рассказывают значения синуса, косинуса, тангенса и котангенса произвольного угла

Учебно-воспитательные задачи:

Образовательная:

Познакомиться со значениями синуса, косинуса, тангенса и котангенса произвольного угла, обеспечить усвоение новых знаний по данной теме, сформировать навыки применения знаний по данной теме

Развивающая: развитие способности выражать мысли, познавательных способностей, формирование алгоритмического мышления, расширение кругозора

Воспитательная: способствовать выявлению, раскрытию способностей учащихся, возбуждать интерес к предмету, побуждать учащихся к применению полученных знаний

Результаты обучения:

Учащиеся знают значения синуса, косинуса, тангенса и котангенса произвольного угла

Учащиеся умеют: применять значения тригонометрических функций в решении задач, ясно выражать мысли, участвовать в дискуссии, умеют слушать и слышать

Этапы урока

Содержание этапа

Оргмомент.

Задачи: обеспечить нормальную внешнюю обстановку на уроке, психологически подготовить детей к общению

Приветствие

Проверка подготовленности к уроку

Организация внимания школьников

Ознакомление с планом проведения урока

Проверка домашнего задания.

Задачи: установить правильность, полноту и осознанность выполнения всеми учащимися домашнего задания, выявить пробелы в знаниях, устранить в ходе проверки обнаруженные пробелы

Выявление степени усвоения заданного учебного материала

Ликвидация обнаруженных недостатков.

Проверка выполнения домашнего задания у доски

Вызов.

Задачи: обеспечить включение школьников в совместную деятельность по определению целей учебного занятия.

Сообщение темы урока

Формулируют цели: сформировать навыки применения знаний по данной теме

Актуализация знаний и умений

Задачи: психологическая подготовка ученика: сосредоточение внимания, осознание значимости предстоящей деятельности, возбуждение интереса к уроку; учащиеся воспроизводят известные им знания, осознают их, обобщают факты, связывают старые знания с новыми условиями, с новыми данными и т.д. 

У доски игра «крестики-нолики»

sin 30° cos 45° tg 0° тg 90° sin 60° cos 0° сos 60° tg 180° sin 0°

tg π/3 sin π/4 tg π/6 sin π/2 cos π/6 tg π/4 cos π/2 cos π sin π

Переведите:60°, 120°, 270°, в радианную меру.

Переведите:90°, 135°, 360°, в радианную меру.

Переведите: π/2, π/4, 3π/4, в градусную меру.

Переведите: π, π/6, 5 π/6, в градусную меру.

Осмысление

Изучение нового материала.

Задачи: обеспечить восприятие, осмысление и первичное запоминание изучаемого материала, осознание своих способов проработки учебной информации

Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов

Тригонометрические определения синуса, косинуса, тангенса и котангенсапозволяют указать значения тригонометрических функций для углов 0 и 90градусов:
 , а котангенс нуля градусов не определен, и
, а тангенс 90 градусов не определен.

В курсе геометрии из прямоугольных треугольников с углами 30, 60 и 90 градусов, а также 45, 45 и 90 градусов находятся значения синуса, косинуса, тангенса и котангенса углов 30, 45 и 60 градусов:

Занесем указанные значения тригонометрических функций для углов 0, 30, 45, 60 и90 градусов (0, π/6, π/4, π/3, π/2 радиан) в таблицу, назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса.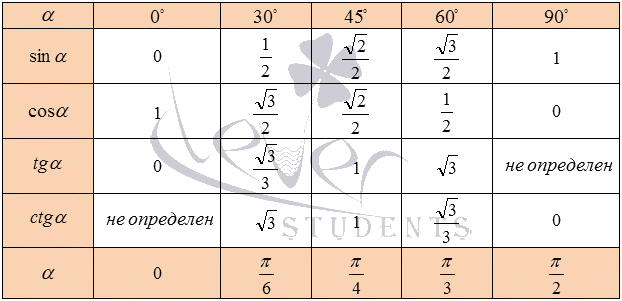

Используя формулы приведения, только что составленную таблицу синусов, косинусов, тангенсов и котангенсов можно расширить, дополнив значениями тригонометрических функций для углов 120, 135, 150, 180, 210, 225, 240, 270, 300,315, 330 и 360 градусов (0, π/6, π/4, π/3, π/2, …, 2π радиан). При этом она принимает следующий вид.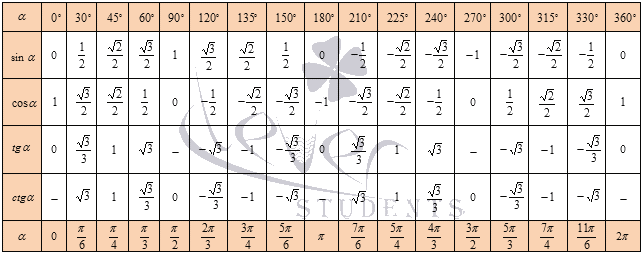

Опираясь на свойство периодичности синуса, косинуса, тангенса и котангенса, таблицу основных значений тригонометрических функций можно расширить еще, заменив углы 0, 30, 45, 60, 90, …, 360 градусов соответственно на , где z – любое целое число. Из такой таблицы можно найти значения для всех углов, которым соответствуют точки единичной окружности, указанные на чертеже ниже.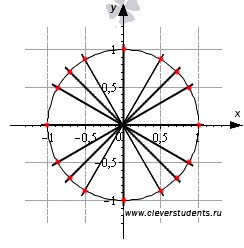

Основные значения тригонометрических функций, собранные в заполненной выше таблице, желательно знать наизусть

Закрепления новых знаний и умений.

Задачи: обеспечить повышение уровня осмысления учащимися изученного материала, глубины его усвоения

tg π/4*cos π/6+2sin45°

4cos60°-3sinπ/2+1/2tg45°

6sin π/2-1,5tg180°-√3cos π/6

√2cos π/4+√3tg30°+1,5cosπ

Проверка новых знаний

Задачи: установить правильность и осознанность учащимися изученного материала, выявить пробелы первичного осмысления

Работа с учебником №369-372

Уровень В № 375,376

Коррекция знаний.

Задачи: скорректировать выявленные проблемы

Организация деятельности учащихся по коррекции выявленных недостатков

Индивидуальное задание.

Повторное разъяснение учителя.

Подведение итогов. Рефлексия.

Задачи: инициировать рефлексию учащихся по поводу своего эмоционального состояния, дать оценку работе отдельных учащихся и всего класса

Мобилизация учащихся на рефлексию

В занятии для меня было:

Самым полезным_________________________________________________

Самым приятным __________________________________________________

самым интересным ______________________________________________

.Выставление оценок.