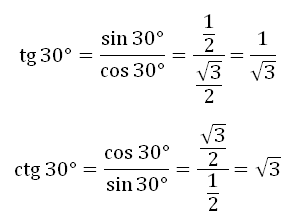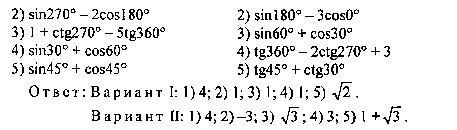Тема урока: Синус, косинус, тангенс и котангенс числа.
Тип урока: Комбинированный.
Цели урока:
- Образовательные: ввести понятие тригонометрических функций синуса, косинуса, тангенса и котангенса, как координат точки единичной окружности; определить множество значении этих функций; рассмотреть перевод градусной меры измерения улов в радианную меру и наоборот; рассмотреть зависимости между косинусом, синусом, тангенсом и котангенсом одного и того же аргумента.
- Развивающие: развивать и совершенствовать умения применять имеющиеся у учащихся знания в различных ситуациях; развивать грамотную математическую речь учащихся, умение давать лаконичные формулировки.
- Воспитательные: воспитывать у учащихся аккуратность, умение слушать, высказывать свое мнение; культуру поведения.
- Оснащение урока: карточки
- Литература: Математика 10 кл.; А.Н.Колмогоров
Ход урока:
1. Организационный момент
Здравствуйте ребята. Садитесь. Проверка готовности к уроку, отсутствующие.
2. Повторение теоретического материала (3 мин.)
А теперь давайте вспомним что мы проходили на прошлом уроке:
Что такое прямой угол? (это угол в 90 градусов)
Что такое острый угол? (это угол от 0 до 90 градусов)
Что такое тупой угол? (это угол от 90 до 180 градусов)
Какой угол называется развернутым? (этот угол равен 180 градусов)
3. Изучение нового материала (30 мин)
Острый угол в прямоугольном треугольнике
Из курса геометрии известны определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. Они даются как отношение сторон прямоугольного треугольника. Приведем их формулировки.
Определение.
Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе.
Определение.
Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе.
Определение.
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.
Определение.
Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему.
Там же вводятся обозначения синуса, косинуса, тангенса и котангенса – sin, cos, tg и ctg соответственно.
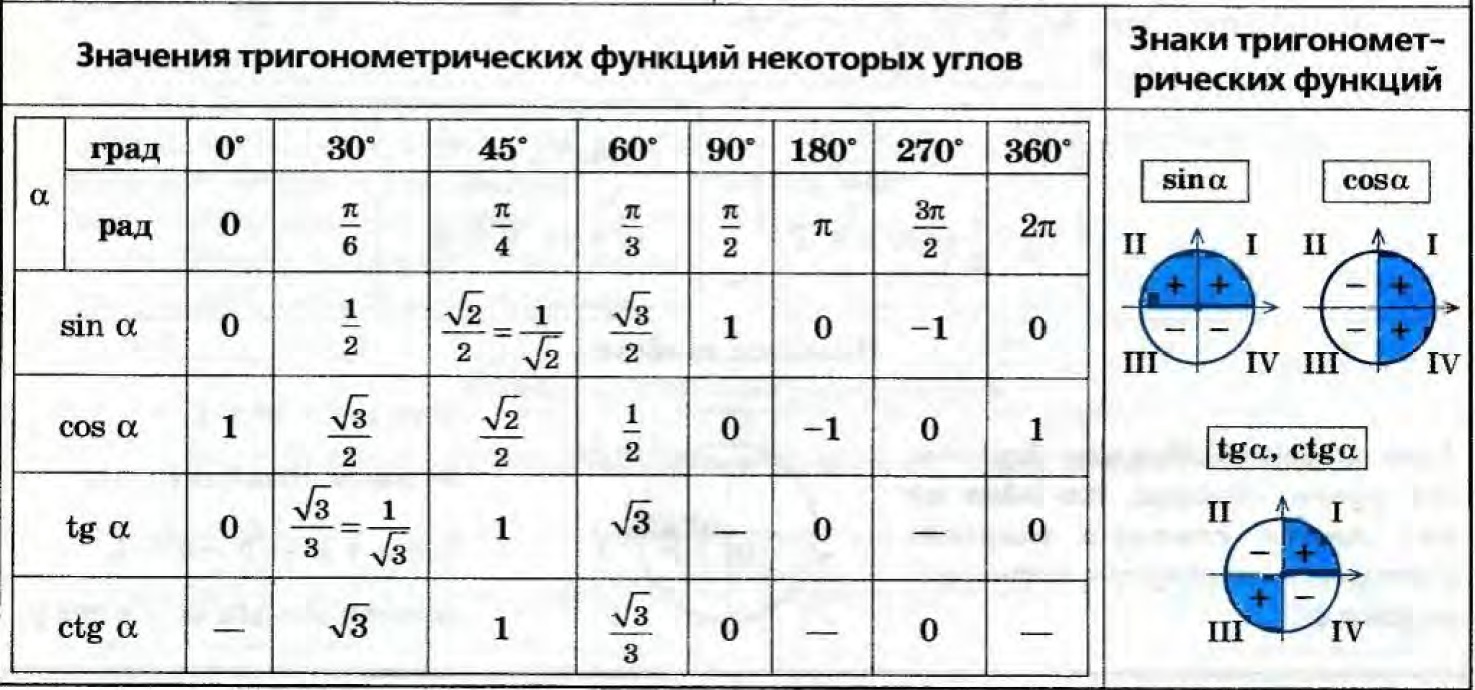
Мы получили значения синуса и косинуса углов от 0 до 90 градусов. Далее, зная формулы тангенса и котангенса:

вы сможете найти значения для указанных углов.
Например:

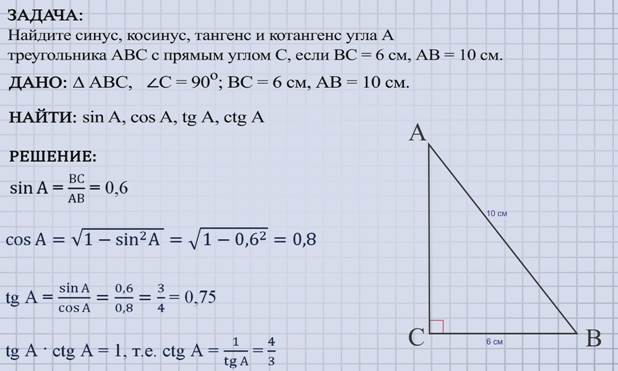
 4.Закрепление Задание№1
4.Закрепление Задание№1

Задание№2:
Найдите числовое значение выражения;
Sin0+cosπ/2+sinπ=0+0+0=0
Просмотр содержимого документа
«Синус, косинус, тангенс и котангенс числа.»
Тема урока: Синус, косинус, тангенс и котангенс числа.
Тип урока: Комбинированный.
Цели урока:
Образовательные: ввести понятие тригонометрических функций синуса, косинуса, тангенса и котангенса, как координат точки единичной окружности; определить множество значении этих функций; рассмотреть перевод градусной меры измерения улов в радианную меру и наоборот; рассмотреть зависимости между косинусом, синусом, тангенсом и котангенсом одного и того же аргумента.
Развивающие: развивать и совершенствовать умения применять имеющиеся у учащихся знания в различных ситуациях; развивать грамотную математическую речь учащихся, умение давать лаконичные формулировки.
Воспитательные: воспитывать у учащихся аккуратность, умение слушать, высказывать свое мнение; культуру поведения.
Оснащение урока: карточки
Литература: Математика 10 кл.; А.Н.Колмогоров
Ход урока:
1. Организационный момент
Здравствуйте ребята. Садитесь. Проверка готовности к уроку, отсутствующие.
2. Повторение теоретического материала (3 мин.)
А теперь давайте вспомним что мы проходили на прошлом уроке:
Что такое прямой угол? (это угол в 90 градусов)
Что такое острый угол? (это угол от 0 до 90 градусов)
Что такое тупой угол? (это угол от 90 до 180 градусов)
Какой угол называется развернутым? (этот угол равен 180 градусов)
3. Изучение нового материала (30 мин)
Острый угол в прямоугольном треугольнике
Из курса геометрии известны определения синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике. Они даются как отношение сторон прямоугольного треугольника. Приведем их формулировки.
Определение.
Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе.
Определение.
Косинус острого угла в прямоугольном треугольнике – это отношение прилежащего катета к гипотенузе.
Определение.
Тангенс острого угла в прямоугольном треугольнике – это отношение противолежащего катета к прилежащему.
Определение.
Котангенс острого угла в прямоугольном треугольнике – это отношение прилежащего катета к противолежащему.
Там же вводятся обозначения синуса, косинуса, тангенса и котангенса – sin, cos, tg и ctg соответственно.
Мы получили значения синуса и косинуса углов от 0 до 90 градусов. Далее, зная формулы тангенса и котангенса:

вы сможете найти значения для указанных углов.
Например:
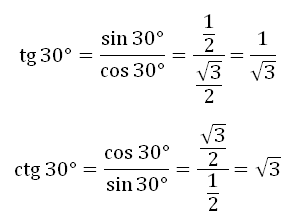
4.Закрепление Задание№1
Задание№2:
Найдите числовое значение выражения;
Sin0+cosπ/2+sinπ=0+0+0=0
Задание№3:
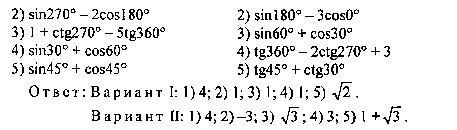
Задание№4:
9. Дом/ задание №6\
10.Итог урока . Ребята, вернемся к теме нашего урока. Над какой темой мы сегодня работали? - Достигли ли мы цели урока?








 4.Закрепление Задание№1
4.Закрепление Задание№1