Дата проведения:
Группа:
Тема урока: Знаки синуса, косинуса и тангенса угла
Преподаватель: Касымова У.Ш.
Тип урока: систематизация знаний.
Цели урока:
1) образовательная: обобщить и проверить знания учащихся о понятиях «синус», «косинус», «тангенс», определении знаков и табличных значений и умения находить значения тригонометрических функций;
2) воспитательная: воспитывать интерес к предмету;
3) развивающая: развивать память, логическое мышление.
Литература: Алгебра и начала математического анализа А.Н.Колмогоров
Ход урока:
I. Организационный момент.
Учитель сообщает тему, цели и задачи урока.
II. Повторение (фронтальная работа с классом).
Устные упражнения
1) Выразить угол в радианах с помощью π.
45°, 150°, 90°, 360°, 30°, 270°, 135°, 60°, 180°, -720°.
3. Новая тема
Число  (пи) – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,14.
(пи) – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,14.
Какие знаки имеют координаты точки в зависимости от их положения в системе координат?
У точек первой четверти 
у точек второй четверти 
у точек третьей четверти 
у точек четвёртой четверти 
В какой координатной четверти находятся точки с указанными координатами


Ответ:
А если точка находится на тригонометрической окружности, то как узнать зависимость знака координат точки от угла поворота вокруг начала координат?
Сегодня на уроке мы узнаем знаки синуса, косинуса, тангенса и котангенса, научимся определять положение точки на тригонометрической окружности в зависимости от комбинации знаков синуса и косинуса, тангенса и котангенса.
1.Рассмотрим единичную окружность в прямоугольной системе координат хОу.

Точка Р(1;0) при повороте вокруг начала координат на угол  переместилась в точку Рₐ. Определим её координаты.
переместилась в точку Рₐ. Определим её координаты.
Синусом угла является ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол
является ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол  .
.
Косинусом угла является абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол
является абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол  .
.
Если угол  то точка Рₐ находится в первой четверти, здесь
то точка Рₐ находится в первой четверти, здесь  , значит
, значит 

Если угол  , то точка Рₐ находится во второй четверти, здесь
, то точка Рₐ находится во второй четверти, здесь  ,
,  , значит ,
, значит ,  .
.
Если угол  , то точка Рₐ находится в третьей четверти, здесь
, то точка Рₐ находится в третьей четверти, здесь  ,
,  , значит
, значит 

Если угол  , то точка Рₐ находится в четвертой четверти, здесь
, то точка Рₐ находится в четвертой четверти, здесь  ,
,  , значит
, значит  ,
, 
На рисунке видно какие знаки имеет синус, а какие косинус.


3.Закрепление Пример1. Определить знаки синуса и косинуса угла .
.
Решение: Выясним, в какой четверти находится точка, полученная поворотом на угол  .
.
 во второй четверти синусы положительны, косинусы отрицательны.
во второй четверти синусы положительны, косинусы отрицательны.
Ответ: 
Пример 2. Определить знаки синуса и косинуса угла  .
.
Решение: Полный угол, при котором точка «обойдёт» всю окружность, равен  .
.
 а это значит, что точка после 2 оборотов окажется в первой четверти, где синус и косинус положительны.
а это значит, что точка после 2 оборотов окажется в первой четверти, где синус и косинус положительны.
Ответ: 
Пример 3.Определить знаки синуса и косинуса угла  .
.
Решение: Угол отрицательный, значит точка получена поворотом по часовой стрелке.
 в 4 четверти синусы отрицательны, косинусы положительны.
в 4 четверти синусы отрицательны, косинусы положительны.
Ответ: синус отрицательный, косинус положительный.
Пример 4. Определить знаки . 
Решение: Знаем, что , а
, а  . Значит,
. Значит,  . Точка во второй четверти.
. Точка во второй четверти.
Ответ: 
2.Знаки тангенса и котангенса.
Тангенс это отношение синуса угла к его косинусу: 
Котангенс это отношение косинуса угла к его синусу:  .
.
Тангенс и котангенс будут положительными там, где синус и косинус имеют одинаковые знаки. Это первая и третья четверти. Синус и косинус имеют разные знаки во второй и четвёртой четвертях, здесь тангенс и котангенс будут отрицательны. На рисунке изображены знаки тангенса и котангенса.

Пример 5.
Определить знак тангенса угла 
Решение  , угол второй четверти
, угол второй четверти
Ответ: tg >
> 0
0
Пример 6
Вывод: чтобы определить знаки синуса, косинуса, тангенса и котангенса, нужно:
- выяснить в какой координатной четверти находится угол;
- знак синусов такой же, как ордината точки (у).
- знак косинусов такой же, как абсцисса точки (х).
- тангенсы и котангенсы положительны там, где синус и косинус имеют одинаковые знаки(1ч. и 4ч.), отрицательны, где синус и косинус имеют противоположные знаки (2ч. и 3ч.).
5.Итог урока
Оценивание
6.Дом/задание. Определить знак тангенса угла  .
.
Просмотр содержимого документа
«Знаки синуса, косинуса и тангенса угла»
Дата проведения:
Группа:
Тема урока: Знаки синуса, косинуса и тангенса угла
Преподаватель: Касымова У.Ш.
Тип урока: систематизация знаний.
Цели урока:
1) образовательная: обобщить и проверить знания учащихся о понятиях «синус», «косинус», «тангенс», определении знаков и табличных значений и умения находить значения тригонометрических функций;
2) воспитательная: воспитывать интерес к предмету;
3) развивающая: развивать память, логическое мышление.
Литература: Алгебра и начала математического анализа А.Н.Колмогоров
Ход урока:
I. Организационный момент.
Учитель сообщает тему, цели и задачи урока.
II. Повторение (фронтальная работа с классом).
Устные упражнения
1) Выразить угол в радианах с помощью π.
45°, 150°, 90°, 360°, 30°, 270°, 135°, 60°, 180°, -720°.
3. Новая тема
Число  (пи) – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,14.
(пи) – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,14.
Какие знаки имеют координаты точки в зависимости от их положения в системе координат?
У точек первой четверти 
у точек второй четверти 
у точек третьей четверти 
у точек четвёртой четверти 
В какой координатной четверти находятся точки с указанными координатами

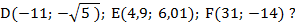
Ответ:
А если точка находится на тригонометрической окружности, то как узнать зависимость знака координат точки от угла поворота вокруг начала координат?
Сегодня на уроке мы узнаем знаки синуса, косинуса, тангенса и котангенса, научимся определять положение точки на тригонометрической окружности в зависимости от комбинации знаков синуса и косинуса, тангенса и котангенса.
1.Рассмотрим единичную окружность в прямоугольной системе координат хОу.
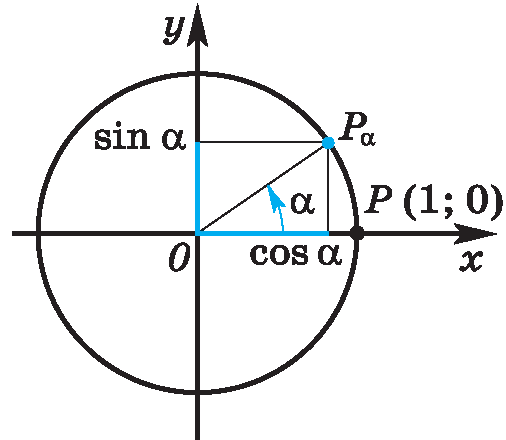
Точка Р(1;0) при повороте вокруг начала координат на угол  переместилась в точку Рₐ. Определим её координаты.
переместилась в точку Рₐ. Определим её координаты.
Синусом угла является ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол
является ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол  .
.
Косинусом угла является абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол
является абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол  .
.
Если угол  то точка Рₐ находится в первой четверти, здесь
то точка Рₐ находится в первой четверти, здесь  , значит
, значит 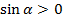
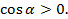
Если угол  , то точка Рₐ находится во второй четверти, здесь
, то точка Рₐ находится во второй четверти, здесь 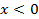 ,
,  , значит ,
, значит , 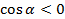 .
.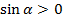
Если угол 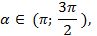 , то точка Рₐ находится в третьей четверти, здесь
, то точка Рₐ находится в третьей четверти, здесь 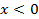 ,
,  , значит
, значит 
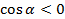
Если угол 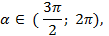 , то точка Рₐ находится в четвертой четверти, здесь
, то точка Рₐ находится в четвертой четверти, здесь 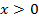 ,
,  , значит
, значит  ,
, 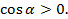
На рисунке видно какие знаки имеет синус, а какие косинус.


3.Закрепление Пример1. Определить знаки синуса и косинуса угла .
.
Решение: Выясним, в какой четверти находится точка, полученная поворотом на угол 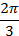 .
.
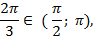 во второй четверти синусы положительны, косинусы отрицательны.
во второй четверти синусы положительны, косинусы отрицательны.
Ответ: 
Пример 2. Определить знаки синуса и косинуса угла  .
.
Решение: Полный угол, при котором точка «обойдёт» всю окружность, равен  .
.
 а это значит, что точка после 2 оборотов окажется в первой четверти, где синус и косинус положительны.
а это значит, что точка после 2 оборотов окажется в первой четверти, где синус и косинус положительны.
Ответ: 
Пример 3.Определить знаки синуса и косинуса угла  .
.
Решение: Угол отрицательный, значит точка получена поворотом по часовой стрелке.
 в 4 четверти синусы отрицательны, косинусы положительны.
в 4 четверти синусы отрицательны, косинусы положительны.
Ответ: синус отрицательный, косинус положительный.
Пример 4. Определить знаки . 
Решение: Знаем, что , а
, а  . Значит,
. Значит,  . Точка во второй четверти.
. Точка во второй четверти.
Ответ: 
2.Знаки тангенса и котангенса.
Тангенс это отношение синуса угла к его косинусу: 
Котангенс это отношение косинуса угла к его синусу:  .
.
Тангенс и котангенс будут положительными там, где синус и косинус имеют одинаковые знаки. Это первая и третья четверти. Синус и косинус имеют разные знаки во второй и четвёртой четвертях, здесь тангенс и котангенс будут отрицательны. На рисунке изображены знаки тангенса и котангенса.

Пример 5.
Определить знак тангенса угла 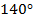
Решение 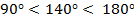 , угол второй четверти
, угол второй четверти
Ответ: tg 0
0
Пример 6
Вывод: чтобы определить знаки синуса, косинуса, тангенса и котангенса, нужно:
выяснить в какой координатной четверти находится угол;
знак синусов такой же, как ордината точки (у).
знак косинусов такой же, как абсцисса точки (х).
тангенсы и котангенсы положительны там, где синус и косинус имеют одинаковые знаки(1ч. и 4ч.), отрицательны, где синус и косинус имеют противоположные знаки (2ч. и 3ч.).
5.Итог урока
Оценивание
6.Дом/задание. Определить знак тангенса угла  .
.
Ответы присылайте на почту.
Укажите Ф.И и группу.
[email protected]






 (пи) – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,14.
(пи) – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,14.






 переместилась в точку Рₐ. Определим её координаты.
переместилась в точку Рₐ. Определим её координаты. является ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол
является ордината точки, полученной поворотом точки (1;0) вокруг начала координат на угол  .
. является абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол
является абсцисса точки, полученной поворотом точки (1;0) вокруг начала координат на угол  .
. то точка Рₐ находится в первой четверти, здесь
то точка Рₐ находится в первой четверти, здесь  , значит
, значит 

 , то точка Рₐ находится во второй четверти, здесь
, то точка Рₐ находится во второй четверти, здесь  ,
,  , значит ,
, значит ,  .
. , то точка Рₐ находится в третьей четверти, здесь
, то точка Рₐ находится в третьей четверти, здесь  ,
,  , значит
, значит 

 , то точка Рₐ находится в четвертой четверти, здесь
, то точка Рₐ находится в четвертой четверти, здесь  ,
,  , значит
, значит  ,
, 

 .
. .
. во второй четверти синусы положительны, косинусы отрицательны.
во второй четверти синусы положительны, косинусы отрицательны.
 .
. .
. а это значит, что точка после 2 оборотов окажется в первой четверти, где синус и косинус положительны.
а это значит, что точка после 2 оборотов окажется в первой четверти, где синус и косинус положительны.
 .
. в 4 четверти синусы отрицательны, косинусы положительны.
в 4 четверти синусы отрицательны, косинусы положительны.
 , а
, а  . Значит,
. Значит,  . Точка во второй четверти.
. Точка во второй четверти.

 .
.

 , угол второй четверти
, угол второй четверти 0
0 .
.



 0
0









