21.05.2020 р. 8 клас. Геометрія. Повторення. Многокутники та їх площі

Чотирикутник, у якого протилежні сторони попарно паралельні, називається паралелограмом.

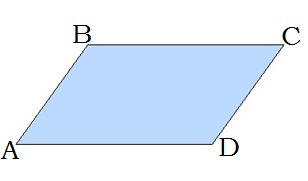
Властивості паралелограма

1. Протилежні сторони паралелограма рівні: AB = DC, BC = AD.

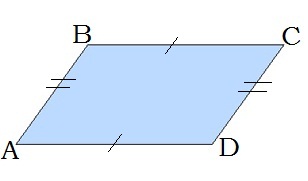
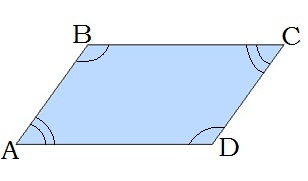
2. Протилежні кути паралелограма рівні: ∠A = ∠C, ∠B = ∠D.

3. Діагоналі паралелограма діляться навпіл точкою перетину: BO = OD, AO = OC.

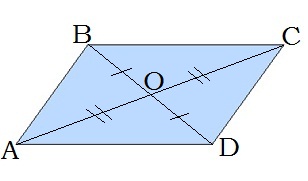
4. Діагональ ділить паралелограм на два рівні трикутники: ABC і CDA.

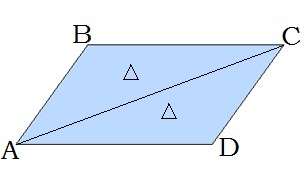
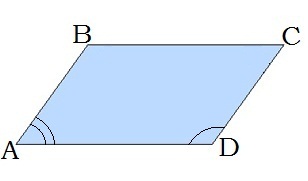
5. Сума кутів, прилеглих до кожної сторони паралелограма, дорівнює 180°. ∠A + ∠D = 180°.

6. Різносторонні кути при діагоналі рівні: ∠BAC = ∠ACD, ∠BCA = ∠CAD.

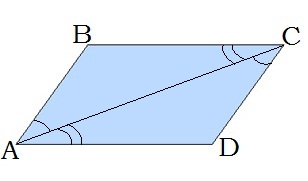
Прямокутником називається паралелограм, у якого всі кути прямі.

Властивості прямокутника

Оскільки прямокутник є паралелограмом, він має всі властивості паралелограма.

1. Протилежні сторони прямокутника рівні: AB = CD, BC = AD.

2. Кожен кут прямокутника дорівнює 90°.

Це означає, що протилежні кути рівні й сума кутів, прилеглих до однієї сторони, дорівнює 180°.

3. Діагоналі прямокутника точкою перетину діляться навпіл: BO = OD, AO = OC.

Крім того, BO = OD = AO = OC (див. шосту властивість).

4. Діагональ прямокутника ділить його на два рівні прямокутні трикутники.

5. Різносторонні кути при діагоналі рівні.

Особлива властивість прямокутника

6. Діагоналі прямокутника рівні: BD = AC.

Використовуючи ознаки ромба, можна визначити, чи є даний чотирикутник або паралелограм ромбом.

1. Якщо діагоналі паралелограма перпендикулярні, то такий паралелограм є ромбом. 2. Якщо дві суміжні сторони паралелограма рівні, то такий паралелограм є ромбом. 3. Якщо діагоналі паралелограма є бісектрисами його кутів, то такий паралелограм є ромбом. 4. Якщо всі сторони чотирикутника рівні, то такий чотирикутник є ромбом.

Квадратом називається прямокутник, у якого всі сторони рівні.

Властивості квадрата

Квадрату притаманні всі властивості паралелограма. Квадрат можна вважати ромбом із прямими кутами або прямокутником із рівними сторонами, тому квадрат має всі властивості ромба і прямокутника.

1. Всі сторони квадрата рівні: AB = BC = CD = AD.

2. Кожен із кутів квадрата дорівнює 90°.

3. Діагоналі квадрата рівні й точкою перетину діляться навпіл: BD = AC; BO = OD = AO = OC.

4. Діагоналі квадрата взаємно перпендикулярні: BD ⊥ AC.

5. Діагоналі квадрата є бісектрисами його кутів: ∠ABD = ∠DBC = ∠BCA = … = 45°.

6. Діагоналі квадрата ділять його на чотири рівні прямокутні рівнобедрені трикутники.

Зверни увагу! Своїх власних особливих властивостей квадрат не має.

Площа паралелограма Необхідно визначити, що таке висота паралелограма. Це перпендикуляр, проведений з будь-якої точки сторони паралелограма до прямої, що містить протилежну паралельну сторону. Зазвичай, висоту проводять з вершини паралелограма. Оскільки паралелограм має дві пари паралельні сторони, тоді він має висоти двох різних довжин. Висота BE, проведена між довгими сторонами, коротше висоти BF, проведеної між короткими сторонами. 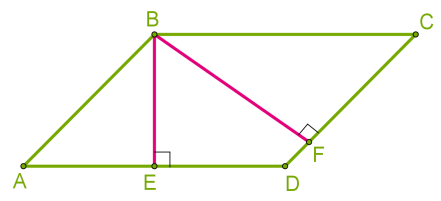Оскільки сторони ромба однакові, тоді висоти ромба також однакові BE = BF. 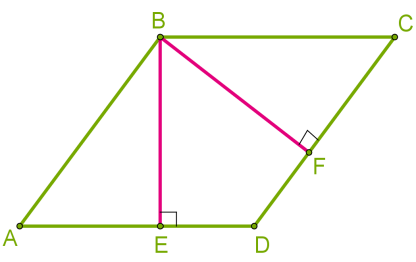Площа довільного паралелограма. Площа паралелограма дорівнює добутку висоти і сторони, до якої проведена висота. 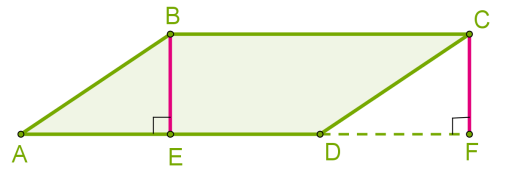Sп−гр = a⋅h. Для визначення площі паралелограма можна використовувати коротку сторону і висоту, проведену до короткої сторони. Площа ромба. Діагоналі ромба в точці перетину діляться навпіл, вони перпендикулярні і ділять ромб на чотири рівних прямокутних трикутника. 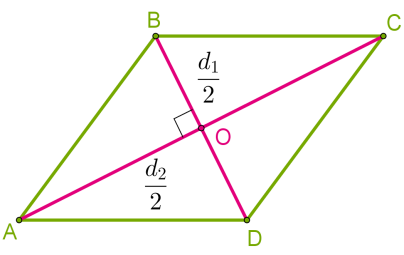Формула визначення площі ромба: Sромба = ½d₁⋅d₂. Ця формула справедлива для визначення площі будь-якого чотирикутника, якщо його діагоналі перпендикулярні. Оскільки діагоналі квадрата рівні, тоді для визначення площі квадрата у формулі достатньо довжини однієї діагоналі: Sквадрата = ½d². Площа довільного трикутника. Оскільки діагональ паралелограма ділить його на два рівних трикутника, тоді площа трикутника дорівнює половині площі паралелограма. 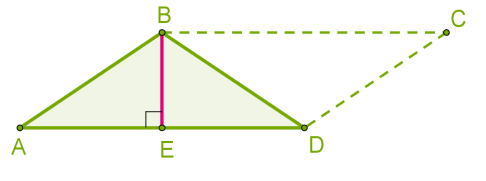Sтрик = ½a·h_а, де h — висота (на малюнку — BE), проведена до сторони a (на малюнку — AD). Для визначення площі трикутника можна використовувати будь-яку сторону і висоту, проведену до цієї сторони. Зручно іноді використовувати формулу Герона, якщо відомі довжини всіх трьох сторін трикутника. SΔ = √p(p−a)(p−b)(p−c), де p = ½(a+b+с) — формула Герона, де a,b і c — сторони трикутника, p — півпериметр трикутника. Площа прямокутного трикутника. Оскільки катети прямокутного трикутника взаємно перпендикулярні, тоді один катет може бути висотою, а інший катет — стороною, до якої проведена висота. Отримуємо формулу: S = ½ a⋅b, де a і b — катети. Площа трапеції. Трапеція має одну пару паралельних сторін, отже, має одну висоту — перпендикуляр, проведений між паралельними сторонами. Найчастіше висоту трапеції проводять з вершин або через точку перетину діагоналей.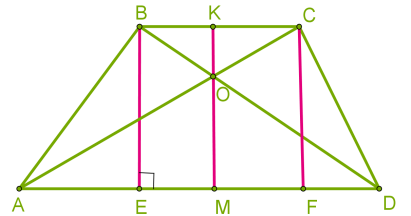 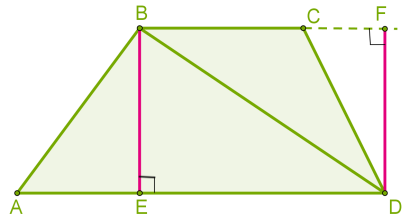S_трап. = ½ (а + b)·h, де a і b - основи трапеції,h - її висота.

21.05.2020 р. Скласти конспект матеріалу. Повторити пункти 19 - 22. Виконати вправу № 857.