07.05.2020 р. 8 клас. Геометрія. Повторення. Теорема Піфагора

Одна з найвідоміших геометричних теорем — теорема Піфагора, знаменитого давньогрецького філософа і математика.

В історії математики знаходимо твердження, що цю теорему знали за багато років до Піфагора, наприклад, стародавні єгиптяни знали про те, що трикутник зі сторонами 3, 4 і 5 є прямокутним.

У наш час теорема звучить так (маючи на увазі не тільки площі, але і довжини сторін прямокутного трикутника):

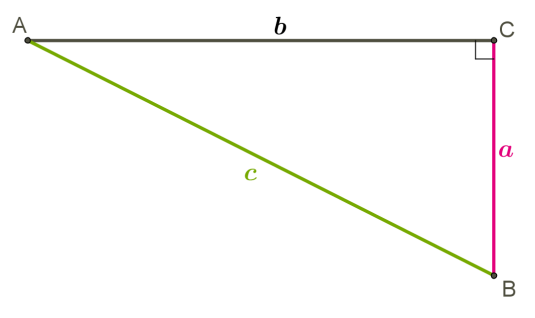
У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів c² = a²+b².

Відомо дуже багато доведень теореми з різними математичними методами, але одні з найбільш наочних пов'язані з площами.

1. Побудуємо квадрат, сторона якого дорівнює сумі катетів даного трикутника a+b. Площа квадрата дорівнює (a+b)²:

2. Якщо провести гіпотенузи c, очевидно, що вони утворили квадрат всередині побудованого квадрата.

Сторони чотирикутника дорівнюють c, а кути — прямі, оскільки гострі кути прямокутного трикутника в сумі дають 90°, тоді кут чотирикутника також дорівнює 90°, тому що разом всі три кута дають 180°.

Отже, площа квадрата складається з чотирьох площ рівних прямокутних трикутників і площі квадрата, утвореного гіпотенузами:

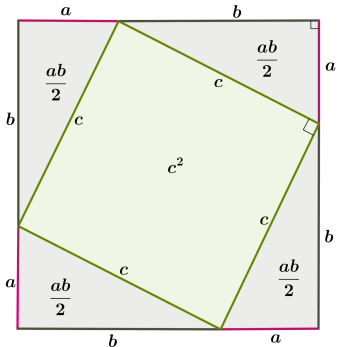
3. На двох сторонах квадрата змінимо місцями відрізки a і b, при цьому довжина сторони квадрата не змінюється. Тепер площу квадрата можемо скласти з двох площ квадратів, утворених катетами a і b і двох площ прямокутників:

4. З цього випливають висновки:

4⋅ab/2 = 2ab і c² = a²+b², що і є одним із доведень теореми Піфагора.

Зверни увагу!

Якщо знаходимо довжину гіпотенузи c, тоді виконуємо додавання квадратів довжин катетів a і b і визначаємо квадратний корінь:

c² = а²+b²; c = √a²+b².

Якщо знаходимо довжину одного катета, тоді виконуємо віднімання довжини квадрата іншого катета від квадрата довжини гіпотенузи і визначаємо квадратний корінь: a² = c²−b²; a = √c²−b².

Зворотна теорема використовується, як ознака прямокутного трикутника.

Якщо квадрат однієї сторони трикутника дорівнює сумі квадратів двох інших сторін, тоді трикутник є прямокутним.

Приклад:

Чи є трикутник зі сторонами 6 см, 7 см і 9 см прямокутним?

Обираємо більшу сторону і перевіряємо, чи виконується теорема Піфагора: 92 = 62+72; 81 ≠ 36+49, отже, цей трикутник не прямокутний.

Чи є трикутник зі сторонами 5 см, 12 см і 13 см прямокутним? Обираємо більшу сторону і перевіряємо, чи виконується теорема Піфагора:

132 = 122+52; 169 = 144+25, отже, цей трикутник прямокутний.

Щоб не витрачати багато часу на розв'язання, корисно запам'ятати найбільш використовувані числа Піфагора:

катет, катет, гіпотенуза: 3; 4; 5 та 6; 8; 10 і 12; 16; 20 та 5; 12; 13.

07.05.2020 р. Скласти конспект матеріалу п. 16. Виконати вправу № 554.