08.05.2020 р. 9 клас. Геометрія. Повторення. Теорема синусів і косинусів. Розв'язуванння трикутників

Теорема синусів

Теорему Піфагора і тригонометричні функції гострого кута можна використовувати для обчислення елементів лише в прямокутному трикутнику.

Для знаходження елементів у довільному трикутнику використовується теорема синусів або теорема косинусів.

Теорема синусів. Сторони трикутника пропорційні синусам протилежних кутів:

a/sinA = b/sinB = c/sinC (під час розв'язання задачі одночасно пишуться дві частини, утворюючи пропорцію).

Теорема синусів використовується для обчислення:

1) невідомих сторін трикутника, якщо відомі два кути і одна сторона;

2) невідомих кутів трикутника, якщо відомі дві сторони і один прилеглий кут.

Оскільки один із кутів трикутника може бути тупим, значення синуса тупого кута знаходиться за формулою:

sin(180°−α) = sinα.

Найчастіше використовуються тупі кути: sin120° = sin(180°−60°) = sin60° = √3/2; sin150° = sin(180°−30°) = sin30° = 1/2; sin135° = sin(180°−45°) = sin45° = √2/2.

Радіус описаного кола

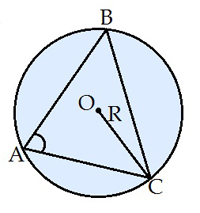
asinA = bsinB = csinC = 2R, де R — радіус описаного кола.

Виразивши радіус, отримуємо R = a/(2sinA), або R = b/(2sinB), або R = c/(2sinC).

Теорема косинусів

Для обчислення елементів прямокутного трикутника достатньо 2 дані величини (дві сторони або сторона і кут).

Для обчислення елементів довільного трикутника необхідно хоча б 3 дані величини.

Теорема косинусів. Квадрат сторони трикутника дорівнює сумі квадратів двох інших сторін мінус подвоєний добуток цих сторін на косинус кута між ними: a² = b² + c² − 2⋅b⋅c⋅cosA.

Також теорема виконується для будь-якої сторони трикутника: b² = a² + c² − 2⋅a⋅c⋅cosB; c² = a² + b² − 2⋅a⋅b⋅cosC.

Теорема косинусів використовується для обчислення:

1) невідомої сторони трикутника, якщо відомі дві сторони і кут між ними;

2) обчислення косинуса невідомого кута трикутника, якщо відомі всі сторони трикутника.

Значення косинуса тупого кута знаходиться за формулою:

cos(180°−α) = −cosα.

Найчастіше використовуються тупі кути: cos120° = cos(180°−60°) = −cos60° = −1/2; cos150° = cos(180°−30°) = −cos30° = −√3/2; cos135° = cos(180°−45°) = −cos45° = −√2/2.

Якщо необхідно знайти наближене значення синуса або косинуса іншого кута або обчислити кут за знайденим синусом чи косинусом, використовується таблиця або калькулятор.

Розв'язати трикутник означає знайти невідомі його сторони та кути за відомими сторонами та кутами. Теореми косинусів і синусів дають змогу розв'язувати будь-який трикутник. Величини кутів будемо знаходити до одиниць, а довжини сторін будемо округлювати до десятих.

08.05.2020 р. Скласти конспект матеріалу пункти 1 - 4. Виконати вправу № 21.4