Геометрическое изображение комплексных чисел. Тригонометрическая форма записи комплексного числа (для ДО)

Тема: «Геометрическое изображение комплексных чисел. Тригонометрическая форма записи комплексных чисел»

1. Продолжаем работать с комплексными числами. Как вы уже поняли, комплексное число можно записать в виде z = x+iy ( или z = x+yi, что в принципе одно и тоже, в разных учебниках может быть записано по разному), а так же может быть использована запись z = a+ib, здесь а- это как х (икс), а b – как у (игрэк). Поэтому и в различных видео-уроках может быть использовано разное обозначение!

2. Перейдём к изучению нового материала. Вот вопросы на которые нужно найти ответ сегодня:

Как геометрически можно изобразить комплексные числа? Какой вид имеет тригонометрическая форма комплексного числа? Ответить на эти вопросы вы сможете, просмотрев видео-урок№1 (2 мин) по ссылке

https://www.youtube.com/watch?v=i9rw7EQ8MPQ, здесь объясняется в доступной форме как именно изображается комплексное число в системе координат (с помощью точки или радиус-вектора). Все объяснения по видео-уроку необходимо записать в тетрадь.

Далее перейдём к видео-уроку№2 (9 мин.) по ссылке https://www.youtube.com/watch?v=oj756X5jCqo, здесь тоже показано изображение комплексных чисел ( далее буду писать сокращенно к.ч.) и выводится тригонометрическая форма к.ч. Так же формулы и объяснения необходимо записать в тетрадь. Материал сложный, но по учебнику разбираться гораздо сложнее. Эта тема не включена в экзаменационную работу, но текущий тест по теме будет.

3. Повторение ранее изученного. Давайте вспомним, как выполняются действия над комплексными числами в алгебраической форме. Для этого посмотрите предыдущий конспект, действия с к.ч. в алгебраической форме.

Пример1. Выполнить действия: а) (2 + 3i)²; б) (3 – 5i)²; в) (5 + 3i)³.

Решение. Воспользуемся формулой «квадрат суммы» и «квадрат разности», «куб суммы» (в предыдущем конспекте мы их записали)

а) (2 + 3i)² = 4 + 2×2×3i + 9i² = 4 + 12i – 9 = – 5 + 12i;

б) (3 – 5i)² = 9 – 2×3×5i + 25i² = 9 – 30i – 25 = – 16 – 30i;

в) (5 + 3i)³ = 125 + 3×25×3i + 3×5×9i² + 27i³;

так как i² = – 1, а i³ = – i ( что такое i³ =i² * i, вместо i² =-1, то -1 умножить на i, получим –i), то по формуле кубов, получим :

(5 + 3i)³ = 125 + 225i – 135 – 27i = – 10 + 198i.

Рассмотрим теперь применение формулы (a + b)(a – b) = a² – b².

Пример2. Выполнить действия: а) (5 + 3i)(5 – 3i); б) (2 + 5i)(2 – 5i); в) (1 + i)(1 – i).

Решение.

а) (5 + 3i)(5 – 3i) = 5² – (3i)² = 25 – 9i² = 25 + 9 = 34;

б) (2 + 5i)(2 – 5i) = 2² – (5i)² = 4 + 25 = 29;

в) (1 + i)(1 – i) = 1² – i² = 1 + 1 = 2.

Пример3. Выполнить деление: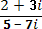

Решение:

Напоминаю, чтобы выполнить деление, нужно числитель и знаменатель умножить на выражение сопряженное для знаменателя, т.е. на (5+7i). Умножим отдельно числитель и знаменатель на (5+7i):

Числитель: (2 + 3i)(5 + 7i) = 10 + 14i + 15i + 21i² = – 11 + 29i;

Знаменатель: (5 – 7i)(5 + 7i) = 25 – 49i² = 25 + 49 = 74.

Итак, получим: 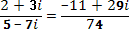. Это ответ.

А теперь, давайте рассмотрим решение квадратных уравнений, дискриминант которых отрицателен. Неожиданно, правда?

Пример4. Решите уравнение: а) x² – 6x + 13 = 0; б) 9x² + 12x + 29 = 0.

Решение:

а) Найдем дискриминант по формуле: D = b² – 4ac.

Так как a = 1, b = – 6, c = 13, то D = (– 6)² – 4×1×13 = 36 – 52 = – 16; D < 0, √-16=√16i²=4i, так как i² – это -1

Корни уравнения находим по формулам: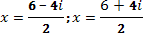

Это ответ.

б) Здесь a = 9, b = 12, c = 29. Следовательно, D = b² – 4ac =12² – 4×9×29 = 144 – 1044 = – 900, √-900=√900i²=30i

Находим корни уравнения: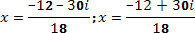

Это ответ.

Вывод! Мы видим, что если дискриминант квадратного уравнения отрицателен, то квадратное уравнение имеет два сопряженных комплексных корня, т.е. корни отличаются только знаком в числителе.

4. Внимание! Домашняя работа: на оценку «3» выполнить 4.1.(1,2,3,4)

«4» выполнить 4.1. (1,2,3,5,7,8) и 4.2.(а)

«5» выполнить 4.1.(1,3,5,7,8,10) и 4.2.(а, в), можно решить все задания (в качестве подстраховки)

4.1.Выполните действия:

1) (3 + 5i) + (7 – 2i) ; 2) (6 + 2i) + (5 + 3i); 3) (– 2 + 3i) - (7 – 2i) ; 4) (2 + 3i) - (5 – 7i); 5) (6 + 4i)×(5 + 2i); 6) (– 2 + 3i)×(3 + 5i); 7) (1 –i)×(1 + i) ; 8) (3 + 5i)² ; 9) (2 – 7i)² ;;10)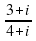

4.2.Решите уравнения: а) x² – 4x + 13 = 0; б) x² + 3x + 4 = 0; в) 4x² – 20x + 26 = 0.

Решение домашней работы отправляем на почту [email protected]. Если есть вопросы- задавайте, пишите на почту.