

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока





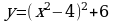 , её ветви направлены вверх (коэффициент при
, её ветви направлены вверх (коэффициент при 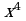 положительный, равен 1); она имеет два минимума в точках
положительный, равен 1); она имеет два минимума в точках 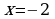 и
и 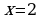
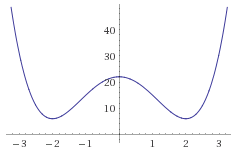
 -координату, а запоминание новой точки минимума происходит только тогда, когда только что вычисленное значение F(t) станет строго меньше, чем хранящееся в переменной R:
-координату, а запоминание новой точки минимума происходит только тогда, когда только что вычисленное значение F(t) станет строго меньше, чем хранящееся в переменной R:









