Математика. Признаки делимости. Примеры.

Признаки делимости чисел– это правила, позволяющие не производя деления сравнительно быстро выяснить, делится ли это число на заданное без остатка.  Некоторые из признаков делимости довольно просты, некоторые сложнее. На этой странице Вы найдете как признаки делимости простых чисел, таких как, например, 2, 3, 5, 7, 11, так и признаки делимости составных чисел, таких, как 6 или 12.

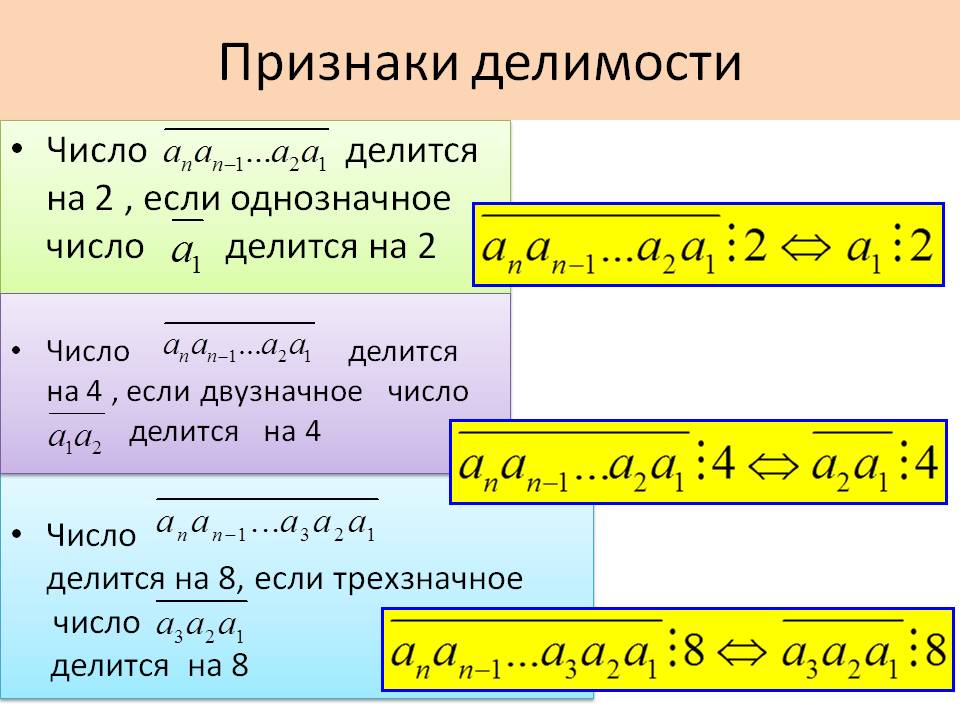
Признак делимости на 2

Это один из самых простых признаков делимости. Звучит он так: если запись натурального числа оканчивается чётной цифрой, то оно чётно (делится без остатка на 2), а если запись числа оканчивается нечётной цифрой, то это число нечётно. Другими словами, если последняя цифра числа равна 2, 4, 6, 8 или 0 - число делится на 2, если нет, то не делится Например, числа: 234, 8270, 1276, 9038, 502 делятся на 2, потому что они чётные. А числа: 235, 137, 2303 на 2 не делятся, потому что они нечетные.

Признак делимости на 3

У этого признака делимости совсем другие правила: если сумма цифр числа делится на 3, то и число делится на 3; если сумма цифр числа не делится на 3, то и число не делится на 3. А значит, чтобы понять, делится ли число на 3, надо лишь сложить между собой цифры, из которых оно состоит. Выглядит это так: 3987 и 141 делятся на 3, потому что в первом случае 3+9+8+7=27 (27:3=9 - делится без остака на 3), а во втором 1+4+1=6 (6:3=2 - тоже делится без остака на 3). А вот числа: 235 и 566 на 3 не делятся, потому как 2+3+5=10 и 5+6+6=17 (а мы знаем, что ни 10 ни 17 не делятся на 3 без остатка).

Признак делимости на 4

Этот признак делимости будет посложнее. Если последние 2 цифры числа образуют число, делящееся на 4 или это 00, то и число делится на 4, в противном случае данное число не делится на 4 без остатка. Например: 100 и 364 делятся на 4, потому что в первом случае число оканчивается на 00, а во втором на 64, которое в свою очередь делится на 4 без остатка (64:4=16) Числа 357 и 886 не делятся на 4, потому что ни 57 ни 86 на 4 не делятся, а значит не соответствуют данному признаку делимости.

Признак делимости на 5

И опять перед нами довольно простой признак делимости: если запись натурального числа оканчивается цифрой 0 или 5, то это число делится без остатка на 5. Если же запись числа оканчивается иной цифрой, то число без остатка на 5 не делится. Это значит, что любые числа, оканчивающиеся цифрами 0 и 5, например 12355 и 430, подпадают под правило и делятся на 5. А, к примеру, 15493 и 564 не оканчиваются на цифру 5 или 0, а значит они не могут делиться на 5 без остатка.

Признак делимости на 6

Перед нами составное число 6, которое является произведением чисел 2 и 3. Поэтому признак делимости на 6 тоже является составным: для того, чтобы число делилось на 6, оно должно соответствовать двум признакам делимости одновременно: признаку делимости на 2 и признаку делимости на 3. При этом обратите внимание, что такое составное число как 4 имеет индивидуальный признак делимости, ведь оно является призведением числа 2 на само себя. Но вернемся к признаку делимости на 6. Числа 138 и 474 чётные и отвечают признакам делимости на 3 (1+3+8=12, 12:3=4 и 4+7+4=15, 15:3=5), а значит они делятся на 6. Зато 123 и 447 хоть и делятся на 3 (1+2+3=6, 6:3=2 и 4+4+7=15, 15:3=5), но они нечётные, а значит не соответсвуют признаку делимости на 2, а следовательно и не соответсвуют признаку делимости на 6.

Признак делимости на 7

Этот признак делимости более сложный: число делится на 7, если результат вычитания удвоенной последней цифры из числа десятков этого числа делится на 7 или равен 0. Звучит довольно запутанно, но на практике просто. Смотрите сами: число 959 делится на 7, потому что 95-2*9=95-18=77, 77:7=11 (77 делится на 7 без остатка). Причем если с полученным во время преобразований числом возникли сложности (из-за его размера сложно понять, делится оно на 7 или нет, то данную процедуру можно продолжать столько раз, сколько Вы сочтете нужным). Например, 455 и 45801 обладают признаками делимости на 7. В первом случае все довольно просто: 45-2*5=45-10=35, 35:7=5. Во втором случае мы поступим так: 4580-2*1=4580-2=4578. Нам сложно понять, делится ли 4578 на 7, поэтому повторим процесс: 457-2*8=457-16=441. И опять воспользуемся признаком делимости, так как перед нами пока еще трехзначное число 441. Итак, 44-2*1=44-2=42, 42:7=6, т.е. 42 делится на 7 без остатка, а значит и 45801 делится на 7. А вот числа 111 и 345 не делятся на 7, потому что 11-2*1=11-2=9 (9 не делится без остатка на 7) и 34-2*5=34-10=24 (24 не делится без остатка на 7). 

Признак делимости на 8

Признак делимости на 8 звучит так: если последние 3 цифры образуют число, делящееся на 8, или это 000, то заданное число делится на 8. Числа 1000 или 1088 делятся на 8: первое оканчивается на 000, у второго 88:8=11 (делится на 8 без остатка). А вот числа 1100 или 4757 не делятся на 8,так как числа 100 и 757 не делятся без остатка на 8.

Признак делимости на 9

Этот признак делимости схож с признаком делимости на 3: если сумма цифр числа делится на 9, то и число делится на 9; если сумма цифр числа не делится на 9, то и число не делится на 9. Например: 3987 и 144 делятся на 9, потому что в первом случае 3+9+8+7=27 (27:9=3 - делится без остака на 9), а во втором 1+4+4=9 (9:9=1 - тоже делится без остака на 9). А вот числа: 235 и 141 на 9 не делятся, потому как 2+3+5=10 и 1+4+1=6 (а мы знаем, что ни 10 ни 6 не делятся на 9 без остатка).

Признаки делимости на 10, 100, 1000 и другие разрядные единицы

Данные признаки делимости я объединил потому, что их можно описать одинаково: число делится на разрядную единицу, если количество нулей на конце числа больше или равно количеству нулей у заданной разрядной единицы. Другими словами, например, мы имеем такие числа: 6540, 46400, 867000, 6450. из них все делятся на 10; 46400 и 867000 делятся еще и на 100; и лишь одно из них - 867000 делится на 1000. Любые числа, у которых количество нулей на конце меньше чем у разрядной единицы, не делятся на эту разрядную единицу, например 60030 и 793 не делятся 100.

Признак делимости на 11

Для того, чтобы выяснить, делится ли число на 11, надо получить разность сумм четных и нечетных цифр этого числа. Если данная разность равна 0 или делится на 11 без остатка, то и само число делится на 11 без остатка. Чтобы было понятнее, предлагаю рассмотреть примеры: 2354 делится на 11, потому что (2+5)-(3+4)=7-7=0. 29194 тоже делится на 11, так как (9+9)-(2+1+4)=18-7=11. А вот 111 или 4354 не делятся на 11, так как в первом случае у нас получается (1+1)-1=1, а во втором (4+5)-(3+4)=9-7=2.

Признак делимости на 12

Число 12 является составным. Его признаком делимости является соответствие признакам делимости на 3 и на 4 одновременно. Например 300 и 636 соответствуют и признакам делимости на 4 (последние 2 цифры это нули или делятся на 4) и признакам делимости на 3 (сумма цифр и первого и втророго числа делятся на 3), а занчит, они делятся на 12 без остатка. А вот 200 или 630 не делятся на 12, потому что в первом случае число отвечает лишь признаку делимости на 4, а во втором - лишь признаку делимости на 3. но не обоим признакам одновременно.

Признак делимости на 13

Признаком делимости на 13 является то, что если число десятков числа, сложенное с умноженными на 4 единицами этого числа, будет кратно 13 или равно 0, то и само число делится на 13.  Возьмем для примера 702. Итак, 70+4*2=78, 78:13=6 (78 делится без остатка на 13), значит и 702 делится на 13 без остатка. Еще пример - число 1144. 114+4*4=130, 130:13=10. Число 130 делится на 13 без остатка, а значит заданное число соответсвует признаку делимости на 13. Если же взять числа 125 или 212, то получаем 12+4*5=32 и 21+4*2=29 соответсвенно, и ни 32 ни 29 не делятся на 13 без остатка, а значит и заданные числа не делятся без остатка на 13.