Построение таблиц истинности логических выражений.
Про обозначения
К сожалению, обозначения логических операций И, ИЛИ и НЕ, принятые в «серьезной» математической логике (,,¬), неудобны, интуитивно непонятны и никак не проявляют аналогии с обычной алгеброй. Автор, к своему стыду, до сих пор иногда путает и . Поэтому на его уроках операция «НЕ» обозначается чертой сверху, «И» – знаком умножения (поскольку это все же логическое умножение), а «ИЛИ» – знаком «+» (логическое сложение).
В разных учебниках используют разные обозначения. К счастью, в начале задания ЕГЭ приводится расшифровка закорючек (,,¬), что еще раз подчеркивает проблему.
Что нужно знать:
¬ A, 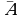 не A (отрицание, инверсия)
не A (отрицание, инверсия)
A B, 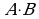 A и B (логическое умножение, конъюнкция)
A и B (логическое умножение, конъюнкция)
A B, 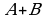 A или B (логическое сложение, дизъюнкция)
A или B (логическое сложение, дизъюнкция)
A → B импликация (следование)
A B эквивалентность (равносильность)
A → B = ¬ A B или в других обозначениях A → B = 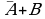
¬ (A B) = ¬ A ¬ B 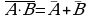
¬ (A B) = ¬ A ¬ B 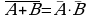
если в выражении нет скобок, сначала выполняются все операции «НЕ», затем – «И», затем – «ИЛИ», «импликация», и самая последняя – «эквивалентность»
таблица истинности выражения определяет его значения при всех возможных комбинациях исходных данных
если известна только часть таблицы истинности, соответствующее логическое выражение однозначно определить нельзя, поскольку частичной таблице могут соответствовать несколько разных логических выражений (не совпадающих для других вариантов входных данных);
количество разных логических выражений, удовлетворяющих неполной таблице истинности, равно 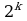 , где
, где 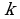 – число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических выражения, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
– число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических выражения, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
логическая сумма A + B + C + … равна 0 (выражение ложно) тогда и только тогда, когда все слагаемые одновременно равны нулю, а в остальных случаях равна 1 (выражение истинно)
логическое произведение A · B · C · … равно 1 (выражение истинно) тогда и только тогда, когда все сомножители одновременно равны единице, а в остальных случаях равно 0 (выражение ложно)
логическое следование (импликация) А→В равна 0 тогда и только тогда, когда из A (посылка) истинна, а B (следствие) ложно
эквивалентность АB равна 1 тогда и только тогда, когда оба значения одновременно равны 0 или одновременно равны 1
Пример задания:
(http://ege.yandex.ru) Дан фрагмент таблицы истинности выражения F. Какое выражение соответствует F?
| x1 | x2 | x3 | x4 | x5 | F |
| 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
Одно из приведенных ниже выражений истинно при любых значениях переменных x1, x2,x3, x4, x5. Укажите это выражение.
1) F(x1,x2,x3,x4,x5)x1
2) F(x1,x2,x3,x4,x5)x2
3) F(x1,x2,x3,x4,x5)x3
4) F(x1,x2,x3,x4,x5)x4
Решение:
во всех заданных вариантах ответа записана импликация, она ложна только тогда, когда левая часть (значение функции F) истинна, а правая – ложна.
выражение 1 ложно для набора переменных в третьей строке таблицы истинности, где F(…) = 1 и 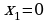 , оно не подходит
, оно не подходит
выражение 2 ложно для набора переменных в третьей строке таблицы истинности, где F(…) = 1 и 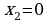 , оно не подходит
, оно не подходит
выражение 3 истинно для всех наборов переменных, заданных в таблице истинности
выражение 4 ложно для набора переменных в первой строке таблицы истинности, где F(…) = 1 и 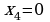 , оно не подходит
, оно не подходит
ответ: 3.







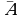 не A (отрицание, инверсия)
не A (отрицание, инверсия)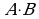 A и B (логическое умножение, конъюнкция)
A и B (логическое умножение, конъюнкция)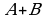 A или B (логическое сложение, дизъюнкция)
A или B (логическое сложение, дизъюнкция)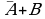
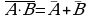
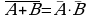
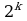 , где
, где 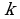 – число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических выражения, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)
– число отсутствующих строк; например, полная таблица истинности выражения с тремя переменными содержит 23=8 строчек, если заданы только 6 из них, то можно найти 28-6=22=4 разных логических выражения, удовлетворяющие этим 6 строчкам (но отличающиеся в двух оставшихся)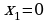 , оно не подходит
, оно не подходит 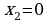 , оно не подходит
, оно не подходит 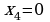 , оно не подходит
, оно не подходит 









