7 кл. Разработка урока "Отрезок. Длина отрезка. Треугольник"

Отрезок. Длина отрезка. Треугольник.

Цели урока:

1) Обучающая: формировать представление о точке, отрезке и многоугольниках, взаимных расположениях точек и отрезка; организовать деятельность, направленную на выполнение учебных заданий на распознавание взаимного расположения точек и отрезков с выполнением соответствующих записей.

2) Развивающая: создать условия для развития навыков изображения и обозначения точек и отрезков.

3) Воспитывающая: содействовать воспитанию аккуратности при изображении рисунков.

Тип урока: изучение нового материала с первичным закреплением.

План урока:

1. Организационный этап.

2. Актуализация опорных знаний.

3. Этап получения новых знаний.

4. Этап обобщения и закрепления нового материала.

5. Рефлексия.

6. Заключительный этап.

Ход урока:

1. Организационный этап.

Здравствуйте. Прежде чем мы приступим к уроку, давайте проверим как вы готовы к уроку. На партах должны лежать: учебник, тетрадь, дневник, ручка, карандаш, линейка и ластик. Все из перечисленных предметов есть у вас?

2. Актуализация опорных знаний:

На доске изображены геометрические фигуры: точка, прямая, отрезок, луч, треугольник, круг, квадрат, прямоугольник.

- Какие из изображенных фигур вам знакомы?

- Какие из них самые простые?

Откройте тетради и запишите число и тему нашего урока.

3. Этап получения знаний:

Тема урока «Отрезок. Длина отрезка. Треугольник». Сегодня на уроке мы поговорим о таком понятии как точка. Научимся строить отрезки. Разберемся, как измерять и сравнивать отрезки, а также познакомимся с многоугольниками.

Простейшей геометрической фигурой является точка. Определение этой геометрической фигуре дать невозможно, но представление о ней каждый из вас знает. Давайте разберемся, что же она из себя представляет. Если посмотреть на звездное небо, то каждая из звезд по отдельности будет представлять нам точку. А самым простым обозначением точки будет след на бумаге от касания заостренным карандашом. Точки принято обозначать большими буквами латинского алфавита: А, В, С, …

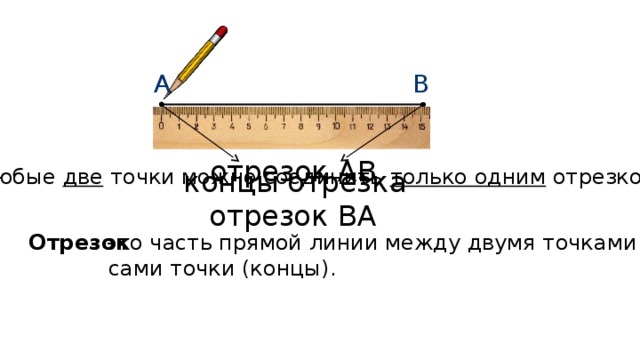
Давайте отметим две точки А и В. Если к двум этим точкам приложить линейку и провести вдоль неё прямую линию от точки А до точки В, то получится отрезок. Его обозначают именами точек, т.е. у нас получился отрезок АВ. Этот же отрезок можно обозначить ВА. Сами же точки А и В называют концами отрезка АВ. Как вы думаете сколько еще отрезков мы можем провести через эти две точки? Любые две точки можно соединить только одним отрезком. И так, запомните определение:

Отрезок – это часть прямой линии между двумя точками включая эти точки (концы).

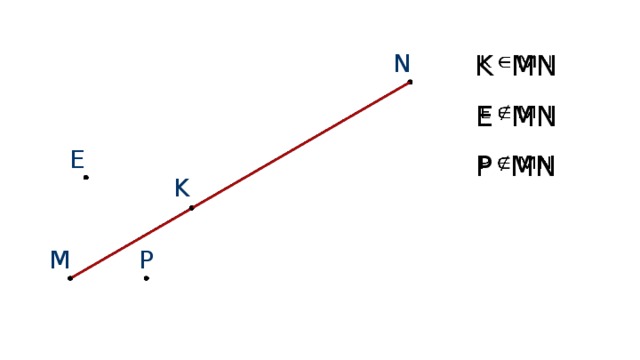
Давайте рассмотрим как могут располагаться точки по отношению к отрезку. Посмотрите на слайд. Изобразим отрезок MN. Поставим точки К, Е и Р, таким образом точку К на отрезок MN, а Е и Р вне его. Точка К лежит на отрезке. Записывают это так К∈NM и говорят точка К принадлежит отрезку MN. Точка К разделяет отрезок MN на 2 отрезка MК и КN. Точки Е и Р не лежат на этом отрезке, поэтому записывают так Е∉MN, Р∉MN, а говорят точки Е и Р не принадлежат отрезку MN

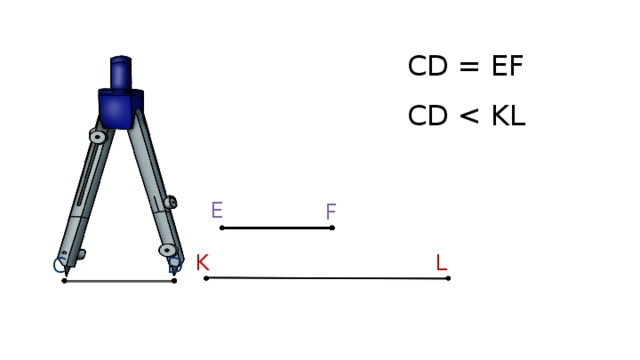
Отрезки можно сравнивать между собой. А сравнивают их при помощи измерителя. Для этого ставят измеритель концами в точки отрезка, а затем прикладывают его к другому отрезку. Если отрезок выходит за пределы концов измерителя, то он больше исходного отрезка, если точки совпадают, значит отрезки равны. А если же отрезок будет находиться между концами измерителя, то он меньше исходного. Посмотрим это на слайде. У нас есть 3 отрезка. Отрезок СD, ЕF и КL. Давайте сравним их. Для этого поставим измеритель концами соответственно в точки С и D. Дальше приложим измеритель к отрезку ЕF. Концы измерителя совпали с точками отрезка. Значит отрезки СD и ЕF равны, записывают это так СD=ЕF. Дальше приложим измеритель к отрезку КL. Отрезок КL выходит за границы измерителя, значит он длиннее отрезка СD. И записывают это так СD

На слайде изображен отрезок РМ его длина 1 см. Отрезок АВ

состоит из трех частей, каждая из которых равна отрезку РМ. Значит

длина отрезка АВ равна 3 см. Пишут: АВ = 3 см.

Длина отрезка АВ – это расстояние между точками А и В.

Кроме сантиметра существуют и другие единицы измерения длины, такие как миллиметр, дециметр, метр, километр и т.д..

Один сантиметр равен десяти миллиметрам: 1 см = 10 мм.

Десять сантиметров называют 1 дециметром: 10 см = 1 дм.

Сто сантиметров равны 1 метру: 100 см = 1 м.

Большие расстояния измеряют в километрах. Например, длина экватора Земли составляет 40 077 км

Один километр равен одной тысяче метров: 1 км = 1000 м.

На слайде изображены три точки А, В и С. Давайте соединим их отрезками. У нас получился треугольник. Обозначают его ∆АВС и говорят треугольник АВС.

Точки А, В и С — называют вершинами треугольника ABC. А отрезки АВ, ВС и АС – сторонами треугольника.

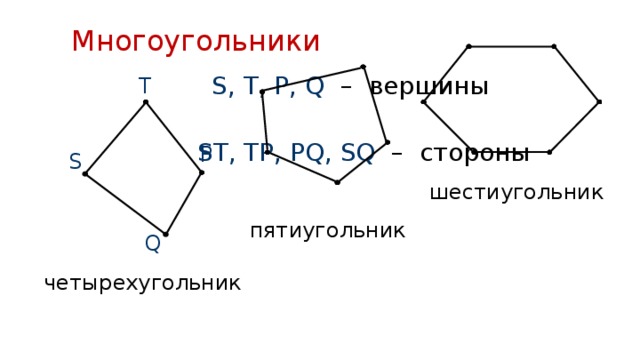
Если соединить 4 точки S,T,P,Q, то мы получим новую фигуру, которая называется четырехугольник STPQ.

Точки S, T, P и Q – называют вершинами четырехугольника STPQ , а отрезки ST, TP, PQ и SQ – сторонами. Если соединить пять точек, то мы получим пятиугольник, шесть точек – шестиугольник и т.д..

Такие фигуры, как треугольник, четырехугольник, пятиугольник и другие, называют многоугольниками.

4. Этап обобщения и закрепления нового материала.

Итак, сделаем основные выводы:

Сегодня на уроке мы с вами разобрались, что из себя представляет точка, как она обозначается; научились чертить отрезки, мерить и сравнивать их. А также познакомились с многоугольниками.

Для закрепления материала ответьте на вопросы:

Как изображается и обозначается точка в математике? Как изображается и обозначается отрезок? Что означает: точка принадлежит отрезку (не принадлежит)? Какие многоугольники вы знаете? Сколько сторон в пятиугольнике? Сколько вершин в треугольнике?

5. Рефлексия.

Хотелось бы узнать, понравился ли вам урок? Что было не понятным на уроке? Что еще бы вы хотели узнать?

6. Домашнее задание: § 1 п. 2 (№ 34, 36, 37, 48)

Дополнительные задания (математический диктант):

№1. Изобразите и обозначьте точку А (отрезок АВ).

№2. Изобразите и обозначьте отрезок CD (точку С).

№3. Начертите четырехугольник АВСD ( пятиугольник EFGHК).

№4.Изобразите точки А и В принадлежащие отрезку CD (точкиE и F не принадлежащие отрезку KL).

Отрезок. Длина отрезка.

Треугольник

• точка

• построение отрезков

• измерение отрезков

• сравнение отрезков

• многоугольники

Точка

A

C

B

B

A

отрезок AB

Любые две точки можно соединить только одним отрезком!

концы отрезка

отрезок BA

– это часть прямой линии между двумя точками и

Отрезок

сами точки (концы).

K MN

N

E MN

E

P MN

K

M

P

CD = EF

CD

E

F

L

K

C

D

P

M

1 cм

A

B

AB = 3 cм

Длина отрезка – это расстояние между точками (концами).

Единицы измерения длины:

миллиметр

1 см = 10 мм

дециметр

10 см = 1 дм

метр

100 см = 1 м

1 км = 1000 м

километр

40 077 км

Треугольник

 ABC

B

A, B, C – вершины

C

AB, BC, AC – стороны

A

Многоугольники

S, T, P, Q – вершины

T

ST, TP, PQ, SQ – стороны

P

S

шестиугольник

пятиугольник

Q

четырехугольник

• представление о точке

• построение отрезков

• измерение отрезков

• сравнение отрезков

• многоугольники