ОТКРЫТЫЙ УРОК ПО ДИСЦИПЛИНЕ МАТЕМАТИКА
Боковая и полная поверхность призмы, пирамиды
Преподаватель математики:
Шаройкина Т.Я.
Калининград
2025
Предмет: Математика
Группа: ИСа24-1. 09.02.07 Информационные системы и программирование
Тема урока: Боковая и полная поверхность призмы, пирамиды
Цель: повторение определений призмы, пирамиды их элементов, ознакомление с понятиями площади поверхности призмы, пирамиды, усеченной пирамиды, формулами вычисления площадей поверхностей многогранников; формирование умений обучающихся применять теоретический материал к решению практических задач.
Формирование познавательных, регулятивных, коммуникативных УУД. Воспитание стремления к сознательному самостоятельному труду. Развитие интереса к предмету. выявление и развитие математических способностей обучающихся.
Задачи урока:
Обобщить и систематизировать сведения о призме, пирамиде, усеченной пирамиде.
Доказать теоремы о площадях боковых поверхностей прямой призмы, правильной пирамиды и правильной усеченной пирамиды.
Применять теоретические знания к решению задач с практическим содержанием.
Вести исследовательскую работу.
Проводить оценку и самооценку знаний и умений.
Тип урока: комбинированный.
Формируемые компетенции:
ОК 01Выбирать способы решения задач профессиональной деятельности применительно к различным контекстам.
ОК 02Использовать современные средства поиска, анализа и интерпретации информации, и информационные технологии для выполнения задач профессиональной деятельности.
ОК 03Планировать и реализовывать собственное профессиональное и личностное развитие, предпринимательскую деятельность в профессиональной сфере, использовать знания по финансовой грамотности в различных жизненных ситуациях.
ОК 04 Эффективно взаимодействовать и работать в коллективе и команде.
ПК 1.1 Формировать алгоритмы разработки программных модулей в соответствии с техническим заданием.
Основные методы, применяемые на уроке:
Оборудование:
техническое: проектор; компьютер, учебная презентация, учебный видеоролик.
дидактическое: карточки для самостоятельной работы, справочный материал, учебник Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 класс. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и другие. - М: Просвещение, 2022.
Внутрипредметные связи: единство терминологии; связь с предыдущим материалом; связь с последующим материалом дисциплины.
Структура урока:
Организационный момент.
2. Актуализация опорных знаний.
3. Изучение нового материала:
3.1 История и практическое применение призмы, пирамиды.
3.2 Площадь полной и боковой поверхности призмы
3.3 Площадь полной и боковой поверхности пирамиды
3.4 Физкультминутка. Кроссворд.
3.5 Площадь полной и боковой поверхности усеченной пирамиды.
4.Закрепление нового материала.
Решение задач
5. Подведение итогов.
Домашнее задание.
Рефлексия.
Ход урока:
1.Организационный момент.
Почему торжественно вокруг?
Слышите, как быстро смолкла речь?
Это о царице всех наук
Поведем сегодня с вами речь.
Неслучайно ей такой почет.
Это ей дано давать ответы,
Как хороший выполнить расчет
Для постройки здания, ракеты.
Есть о математике молва,
Что она в порядок ум приводит.
Потому хорошие слова
Часто говорят о ней в народе.
Ты нам, математика, даешь
Для победы трудностей закалку.
Учится с тобою молодежь
Развивать и волю, и смекалку.
Приветствие. Отметка отсутствующих. Сегодня мы продолжаем изучать многогранники. С какими многогранниками вы познакомились на предыдущих уроках? Комната является призмой? Как рассчитать сколько необходимо купить обоев, чтобы обклеить комнату, в которой вы проживаете. -Что для этого нам необходимо знать? Представьте, что нам надо покрыть железом крышу дома, которая имеет форму правильной 4- угольной пирамиды. Что для этого надо найти? Сформулируйте тему урока. Запишите в тетрадь Боковая и полная поверхность призмы, пирамиды.
2.Актуализация опорных знаний.
У вас на столах листы самооценки знаний, в которые вы будете ставить себе баллы за правильно выполненные задания.
Проверка домашнего задания.
Проведение устного фронтального опроса:
На столе многогранники, выбрать призмы и пирамиды.
| Египтяне их сложили И так ловко смастерили, Что стоят они веками. Догадайтесь-ка, сами Что же это за тела, Где вершина всем видна? Догадались? Из-за вида Всем известна…(пирамида) | Это, вроде бы, ведро.
Но, совсем другое дно
Не кружок, а треугольник
Или даже шестиугольник.
Очень тело уж капризно
Потому что это… (призма).
|
- Дайте определение призмы, пирамиды, усеченной пирамиды.
- Назовите элементы призмы, пирамиды.
- Какие виды призм бывают? Какие виды пирамид бывают?
-Что значит прямая призма?
-Какая призма называется правильной? Какая пирамида называется правильной?
- Дайте определение апофемы.
Проведение самостоятельной работы с последующей самопроверкой.
Тест.
1 вариант.
1). Призма – это выпуклый многогранник, который состоит из:
а) многоугольника и нескольких параллелограммов
б) двух равных многоугольников и нескольких параллелограммов
в) двух равных многоугольников, лежащих в параллельных плоскостях,
и n параллелограммов
2). В основании призмы лежит:
а) любой выпуклый многоугольник
б) только правильный многоугольник
в) любой многоугольник или окружность
3). Призма является прямой, если:
а) боковые ребра перпендикулярны основаниям
б) основания – правильные многоугольники
в) некоторые боковые грани – квадраты
4). Призма является правильной, если:
а) в основании лежит правильный многоугольник
б) боковые грани перпендикулярны основаниям
в) она прямая и в основании лежит правильный многоугольник
5). Высотой прямой призмы можно считать:
а) ребро основания
б) боковое ребро
в) любой отрезок, перпендикулярный основанию
6). Определение пирамиды
а) Многогранник, составленный из двух п-угольников и п-треугольников.
б) Многогранник, составленный из двух равных п-угольников, расположенных в параллельных плоскостях, и п параллелограммов.
в) Многогранник, составленный из одного п-угольника и п-треугольников.
г) Многогранник, составленный из двух равных п-угольников и п-треугольников.
7). Определение апофемы.
а) Высота грани пирамиды.
б) Высота боковой грани правильной пирамиды.
в) Высота боковой грани пирамиды.
г) Высота грани правильной пирамиды.
8). Сколько боковых граней имеет треугольная пирамида
а) Одну.
б) Две.
в) Три.
г) Много
9). Какая фигура не может быть в основании пирамиды?
а) Трапеция
б) Круг.
в) Треугольник.
г) Квадрат.
2 вариант.
1). Призма – это выпуклый многогранник, который состоит из:
а) двух равных многоугольников, лежащих в параллельных плоскостях,
и n параллелограммов
б) двух равных многоугольников и нескольких параллелограммов
в) многоугольника и нескольких параллелограммов
2). В основании призмы лежит:
а) только правильный многоугольник
б) любой многоугольник или окружность
в) любой выпуклый многоугольник
3). Призма является прямой, если:
а) некоторые боковые грани – квадраты
б) боковые ребра перпендикулярны основаниям
в) основания – правильные многоугольники
4). Призма является правильной, если:
а) в основании лежит правильный многоугольник
б) она прямая и в основании лежит правильный многоугольник
в) боковые грани перпендикулярны основаниям
5). Высотой прямой призмы можно считать:
а) боковое ребро
б) любой отрезок, перпендикулярный основанию
в) ребро основания
6). Что представляет собой боковая грань пирамиды?
а) Параллелограмм
б) Круг
в) Прямоугольник
г) Треугольник
7). Определение правильной пирамиды
а). Прямая пирамида называется правильной, если в основании лежит правильный многоугольник.
б). Пирамида называется правильной, если в основании лежит правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
в). Пирамида называется правильной, если отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
г). Пирамида называется правильной, если в основании лежит многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является ее высотой.
8) Что представляет собой боковая грань правильной пирамиды?
а) Равносторонний треугольник
б) Квадрат
в). Прямоугольник
г) Равнобедренный треугольник
9). Сколько оснований имеет правильная пирамида?
а). Одно.
б). Два.
в). Три.
г) Много.
Самопроверка по ответам на доске и выставление баллов в листок самооценки знаний. Каждое задание 1 балл.
3. Изучение нового материала.
3.1. (Подготовил один из обучающихся, презентация) Термин «Призма» греческого происхождения и буквально означает «отпиленное» тело. В памятниках вавилонской и древнеегипетской архитектуры встречаются такие геометрические фигуры, как куб, параллелепипед, призма. Башня ветров в Афинах является выдающимся памятником архитектуры поздней греческой античности.
Одна из версий происхождения термина пирамида утверждает, что название происходит от греческого слова «пир» огонь т.к. форма пирамиды напоминает форму пламени. В архитектуре пирамида широко используется для создания монументальных сооружений, таких как пирамиды в Египте или храмы в Мексике. Ее стройная форма и прочная конструкция делают ее идеальным выбором для создания зданий, которые должны выдерживать тяжелые нагрузки и противостоять времени. Пирами́да Хео́пса или Великая пирамида Гизы — крупнейшая из египетских пирамид, памятник архитектурного искусства Древнего Египта; единственное из «Семи чудес света», сохранившееся до наших дней, и самое древнее из них: её возраст оценивается примерно в 4500 лет. Высота изначально 147м..Вес 6400000т.До 1889г. была самым высоким зданием пока не построили Эйфелеву башню.
Размеры сооружения поразительны даже по современным меркам. Площадь основания способна вместить 10 футбольных полей- 53000м2. Длина основания 230м.
Кроме того, стоит упомянуть о практическом применении знаний о площади поверхности многогранников. Эти знания необходимы в различных областях, таких как архитектура, инженерия, дизайн и даже экология. Например, при проектировании зданий важно знать, сколько материала потребуется для покрытия стен, что напрямую зависит от площади поверхности. Также в упаковке товаров площадь поверхности играет ключевую роль в определении количества материалов, необходимых для упаковки продукта, чтобы обеспечить его безопасность и сохранность
Примеры моделей призмы, которые можно встретить в реальной жизни, включают такие объекты, как базальтовые колонны, кристаллы поваренной соли, пчелиные соты, торты, детские игрушки, шкафы, холодильники, чемоданы и многие другие. В профессиях призма может использоваться при создании архитектурных моделей, дизайне интерьеров, в графическом дизайне и в процессе изучения геометрии.
Сейчас мы часто встречаем пирамиду на улице в виде элементов зданий или самих архитектурных построек. Это очень модно и придаёт зданию некоторый шик.
3.2 Площадь полной и боковой поверхности призмы.
Определение площади полной и боковой поверхности призмы. Как найти площадь боковой поверхности прямой призмы? Обучающиеся выводят формулы, затем открывают учебник и конспектируют учебный материал.
Учебник. Стр.68. Площадь полной поверхности призмы, площадь боковой поверхности призмы. Теорема о площади боковой поверхности прямой призмы.
3.3 Площадь полной и боковой поверхности пирамиды.
Определение площади полной и боковой поверхности пирамиды. Как найти площадь боковой поверхности правильной пирамиды? Обучающиеся выводят формулы, затем открывают учебник и конспектируют учебный материал.
Учебник стр.73-74. Площадь полной поверхности пирамиды, площадь боковой поверхности пирамиды. Теорема о площади боковой поверхности правильной пирамиды.
3.4 Физкультминутка. Кроссворд.
Представьте, что вы – красивые и стройные пирамиды. Потянитесь руками к вашей вершине, вдох. Плавно, через стороны, опускаем руки вниз и тянемся к основанию, выдох. А теперь показываем, какое широкое применение призмы, пирамиды в окружающем мире, руки в стороны, вдох. Исходное положение, выдох. Движения повторяем.
Кроссворд по теме «Многогранники»
Вопросы к кроссворду.
1. Фигура, состоящая из многоугольника и n треугольников.
2. Концы рёбер.
3. Высота боковой грани правильной пирамиды.
4. Фигура, являющаяся боковой гранью пирамиды.
5. Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания призмы.
6. Основание призмы.
7. Какой величины не хватает в формуле 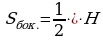 .
.
8. Фигура, являющаяся боковой гранью усечённой пирамиды.
9. Отрезок, соединяющий две вершины, не принадлежащие одной грани.
10. Многоугольники, из которых составлен многогранник.
11. Для какой фигуры вычисляется объём по формуле 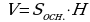 .
.
12. Правильный многогранник, состоящий из 8 равносторонних треугольников.
|
|
| 1 |
|
|
| м |
|
|
|
|
|
|
|
| 2 |
|
|
|
| н |
|
|
|
|
|
|
|
|
|
|
| 3 |
| о |
|
|
|
|
|
|
|
|
| 4 |
|
|
| г |
|
|
|
|
|
|
|
|
|
|
| 5 |
| о |
|
|
|
|
|
|
| 6 |
|
|
|
|
| г |
|
|
|
|
|
|
|
|
|
|
| 7 |
| р |
|
|
|
|
|
|
|
|
|
|
| 8 |
| а |
|
|
|
|
|
|
|
| 9 |
|
|
|
| н |
|
|
|
|
|
|
|
|
|
| 10 |
|
| н |
|
|
|
|
|
|
|
|
|
|
| 11 |
| и |
|
|
|
|
|
|
|
|
|
|
|
| 12 | к |
|
|
|
|
|
|
3.5 Площадь полной и боковой поверхности усеченной пирамиды.
Определение площади полной и боковой поверхности усеченной пирамиды. Как найти площадь боковой поверхности правильной усеченной пирамиды? Обучающиеся выводят формулы, затем открывают учебник и конспектируют учебный материал. Учебник стр.75
4. Закрепление нового материала.
1. Вычислить площадь боковой поверхности пирамиды Хеопса, если
сторона основания –230м., высота – 138м.
2. Коллекционер заказал аквариум, имеющий форму правильной шестиугольной призмы. Сколько квадратных метров стекла необходимо для изготовления аквариума, если сторона основания 0,5 м, а высота 1,2 м? Ответ округлите до сотых.
3. На заводе выпускают подарочные коробки в виде прямой призмы, в основании которой лежит ромб с диагоналями 24 см и 10 см. Площадь полной поверхности призмы равна 760 кв. см. Какой будет высота этой коробки?
4. На даче нужно покрасить с внешней и внутренней стороны бак с крышкой для воды. Бак имеет форму прямой призмы высотой 1,5 м. В основании призмы лежит прямоугольный треугольник с катетами 0,6 м и 0,8 м. В магазине имеется краска в банках по 1 кг и 2,5 кг. Сколько и каких по массе банок краски надо купить для покраски бака, если на 1 квадратный метр расходуется 0,2 кг краски?
5. Палатка имеет форму правильной четырёхугольной пирамиды, сторона основания которой равна 2 м, а высота — 1,5 м. Сколько квадратных метров ткани необходимо, чтобы сшить саму палатку и ее основание, если на швы и обрезки еще дополнительно тратится 10 % от необходимого количества ткани?
6. Представим себе, что мы работаем в экономическом отделе предприятия по изготовлению упаковок для сока. Необходимо просчитать, какая упаковка будет экономически выгодна для производства: упаковка, имеющая форму правильного тетраэдра или упаковка, имеющая форму прямоугольного параллелепипеда.
1 вариант
| Кол-во
упаковок | Длина
(а) | Ширина
(b) | Высота
(h) |
Sосн.
| Sбок.пов. | Sполн.пов. |
| 1 | 6 см | 4 см | 8,5 см | |
|
|
2 вариант
| Кол-во
упаковок | Сторона
грани
(b) | Sполн.пов. для правильного тетраэдра a2√3 |
| 1 | 12 см |
|
Ребята озвучивают свои решения и делают вывод
Экономия составит: на 1 упаковке – ≈31см2;
Вывод: экономически более выгодна будет упаковка, имеющая форму прямоугольного параллелепипеда. Поэтому в магазинах упаковку в виде правильного тетраэдра можно встретить очень редко.
7.Самостоятельная работа.
Вариант 1
1). Площадь полной поверхности призмы – это:
а) сумма площадей всех боковых граней
б) сумма площадей двух оснований
в) сумма площадей всех её граней
2). Площадь боковой поверхности прямой призмы можно найти по формуле:
а) Sбок=Sосн·h
б) Sбок=а·h, где а – сторона основания
в) Sбок=Росн·h
3). Площадь полной поверхности прямой призмы можно найти по формуле:
а) Sполн=Sосн+ Sбок
б) Sполн=2Sосн+ Sбок
в) Sполн=2Росн+ Sбок
4). Крыша башни имеет вид правильной четырехугольной пирамиды, у которой сторона основания равна 12 м, а высота 18 м. Сколько понадобится плиток на покрытие этой крыши, если каждая плитка имеет вид прямоугольника со сторонами 22 см и 18 см.
Вариант 2
1). Площадь полной поверхности пирамиды – это:
а) сумма площадей всех боковых граней
б) сумма площадей двух оснований
в) сумма площадей всех её граней
2). Площадь боковой поверхности правильной пирамиды можно найти по формуле:
а) Sбок=Sосн·h
б) Sбок=а·h, где а – сторона основания
в) Sбок=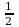 Росн·l , где l- апофема
Росн·l , где l- апофема
3). Площадь полной поверхности пирамиды можно найти по формуле:
а) Sполн=Sосн+ Sбок
б) Sполн=2Sосн+ Sбок
в) Sполн=2Росн+ Sбок
4.Задача. Крыша имеет форму пирамиды с квадратным основанием 6 м х 6 м и высотой 4 м. Сколько листов железа размером 70 см х 140 см нужно для покрытия крыши, если на отходы нужно добавить 10% площади крыши?
Самопроверка по ответам на слайде презентации. Выставление баллов в листок самооценки.
5. Подведение итогов.
Домашнее задание.
Рефлексия.
Домашнее задание: Дома придумать задачу практического содержания на тему «Площадь поверхности призмы, пирамиды».
Сдаем листы самооценки знаний:
Ф.И._________________________________________________
| Виды деятельности на уроке | Максимальное количество баллов | Набранные баллы |
| Домашняя работа | 1 |
|
| Устная разминка | 1 и больше |
|
| Тест №1 | 9 |
|
| Подготовленный материал к уроку | 3 |
|
| Доказательство теорем | 1 и больше |
|
| Кроссворд | 12 |
|
| Решение задач | 6 |
|
| Тест №2 | 4 |
|
| Всего баллов: | 30-36- «5» 24-29- «4» 15-23 - «3» |
|
|
| Оценка |
|
Выводы (выводы делают обучающиеся).
Мы повторили теоретический материал по теме «Многогранники», вывели теоремы о площадях поверхностей многогранников, решили задачи практического содержания и делаем вывод, что площадь поверхности многогранников имеет множество практических применений. Полученные знания позволят нам решать реальные задачи и принимать обоснованные решения в проектировании, строительстве и компьютерной графике.
Заполняется таблица:
| № | Вопрос | Ответ ( + или - ) |
| 1 | Комфортно ли вам было на уроке? | . |
| 2 | Поняли ли вы материал урока? | . |
| 3 | Требовалась ли вам помощь: а) учителя б) учебника в) соседа по парте? |
. . . |
| 4 | Оцените свою работу на уроке по пятибалльной системе. | . |







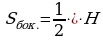 .
.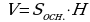 .
.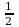 Росн·l , где l- апофема
Росн·l , где l- апофема









