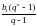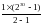Конспект урока алгебры в 9 классе
Тема: Формула суммы n первых членов геометрической прогрессии
Подготовила учитель первой квалификационной категории Икковской основной школы Чебоксарского района Чувашской Республики Федотова Юлия Тимофеевна
Девиз: «Мало знать, надо уметь этим пользоваться»
Цели: 1. Расширить и углубить знания о прогрессиях, продолжить формирование у
учащихся умения применять формулу суммы n- первых членов геометрической прогрессии.
Способствовать развитию наблюдательности, умения анализировать, применять приемы сравнения, переноса знаний в новую ситуацию; развитию логического мышления, творческих способностей учащихся путем решения межпредметных задач.
Побуждать учащихся к преодолению трудностей, самоконтролю, взаимоконтролю. Воспитывать познавательную активность, стремления
расширять свой кругозор.
Тип урока: комбинированный.
1.Вопросы по проверке теоретического уровня знаний.
Какая последовательность называется арифметической прогрессией?
какая последовательность называется геометрической прогрессией?
Как вычислить разность арифметической прогрессии ?
Как вычислить знаменатель геометрической прогрессии?
Почему прогрессия называется арифметической?
Почему прогрессия называется геометрической?
Какому множеству чисел принадлежит число п ?
Запишите формулу суммы n первых членов геометрической прогрессии (q≠1):
если известен первый член и знаменатель геометрической прогрессии;
если известен первый n член и знаменатель.
2. Математический диктант
1.У арифметической прогрессии первый член равен 5, второй член 7.
Найти разность d.
2. У арифметической прогрессии первый член равен 4, второй член 1.
Найти третий член.
3.У геометрической прогрессии первый член 10, второй 5. Найти знаменатель q.
4. У геометрической прогрессии первый член 6, второй 3. Найти третий член.
5. Найти десятый член арифметической прогрессии, если ее первый член равен 1,
а разность d=3.
6.Найти четвертый член геометрической прогрессии, если ее первый член 1,
а знаменатель q= -2.
7. (Физика) Имеется радиоактивное вещество массой 256 г, масса которого
за сутки уменьшается вдвое. Какова станет масса вещества на вторые сутки? На третьи?
8.(Биология) Бактерия за 1 секунду делится на три. Сколько бактерий
будет в пробирке через 5 секунд?
Найти сумму пяти первых членов геометрической прогрессии,
если ее первый член равен -1, а знаменатель 2.
Найти сумму первых четырех членов геометрической прогрессии: 2; -6;
Ответы
1 d=2
2. а3 =-2
3. q=1/2
4. b3=1,5
5. a10=28
6. b4=-8
7. 128, 64
8. 243
9. 31
10. -40
3.Сейчас я вам предлагаю прорешать задачи.
Для их решения потребуются формулы, которые мы с вами повторили.
№651 (б),
№653(б).
4.Задания из сборника предназначенного для подготовки к итоговой аттестации в новой форме по алгебре в 9 классе.


5.Историческая справка
Сами по себе прогрессии известны так давно, что конечно, нельзя говорить о том, кто их открыл. Ведь уже натуральный ряд есть арифметическая прогрессия с первым членом, равным 1, и разностью, тоже равной 1. О том, как давно была известна геометрическая прогрессия, свидетельствует знаменитое предание о создании шахмат.
6.Проверка домашнего задания
В старинной арифметике Магницкого приведена следующая забавная задача.
Некто продал лошадь за 156 руб.Но покупатель, приобретая лошадь, раздумал ее покупать и возвратил продавцу, говоря:
- Нет мне расчета покупать за эту цену лошадь ,которая таких денег не стоит.
Тогда продавец предложил другие условия:
- Если по – твоему, цена лошади высока, то купи ее подковные гвозди; лошадь же тогда получишь в придачу бесплатно. Гвоздей в каждой подкове 6. За первый гвоздь дай мне всего ¼к., за второй ½к., за третий 1к. и т.д.
Покупатель, соблазненный низкой ценой и желая даром получить лошадь, принял условие продавца, рассчитывая, что за гвозди придется уплатить не более 10р.
На сколько рублей покупатель проторговался?
Решение.
Дано:
геометрическая прогрессия
b1=1
q=2
Найти:
S30
Решение:
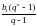
Sn=
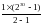
S30= = 230 -1 = 1073741824 -1 =
= 1073741823 коп = 10737418 руб 23 коп
купец получил 3000000 руб
мужик - 10737418 руб 23 коп
разница составляет 7737418 РУБ 23 КОП !!!
Так кому выгодна эта сделка?
7.Выступление ученика . На связь между прогрессиями первым обратил внимание великий Архимед. В печати же эти мысли отчетливо прозвучали лишь в 1544 г., когда вышла книга немецкого математика Михаила Штифеля «Общая арифметика». Штифель составил такую таблицу
| -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
|
| 1/16 | 1/8 | 1/4 | 1/2 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
В верхней строчке написана арифметическая прогрессия с разностью 1. В нижней строчке – геометрическая прогрессия со знаменателем 2.
Пример №1. Надо умножить ½ на 128. Обращаем внимание, что в таблице над ½ написано -1, а над 128 написано 7. Сложим эти числа, получим 6, а под шестеркой читаем 64. Это и есть искомое произведение.
Пример №2. Разделим 32 на 8. Обращаем внимание, что в таблице над 32 написано 5, а над 8 написано 3. Вычтем эти числа 5-3, получим 2, а под двойкой читаем 4. Это и есть искомое
Заметим, что с помощью таблицы можно возводить в степень и извлекать корни. Например, чему равно 43? Против 4 читаем 2, умножаем 2 на 3, получаем 6, против 6 читаем 64, значит, 43 = 64. А чему равен корень четвертой степени из 256? Делим 8 на 4, против 2 читаем 4, значит, корень четвертой степени из 256 равен 4.
Если вспомнить тождества аm ×an=am+n и am:an=am-n, то нижнюю строчку таблицы Штифеля можно переписать так:
|
1/16 |
1/8 |
1/4 |
1/2 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
|
|
| 2-4 | 2-3 | 2-2 | 2-1 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
Теперь можно увидеть, что если показатели степени составляют арифметическую прогрессию, то сами степени составляют геометрическую прогрессию
8.Итог урока.
1.Что нового узнали на уроке?
2.Запишите формулу суммы n первых членов геометрической прогрессии (q≠1): если известен первый член и знаменатель геометрической прогрессии; если известен первый n член и знаменатель.
3. Ответьте на вопрос: «Что каждого из вас получается хорошо при решении задач ?»
ДОМАШНЕЕ ЗАДАНИЕ
П. 28, № 654,656, 658;
примеры применения геометрической прогрессии в жизни (оформить в электронном виде).
А также прошу вас ответить на следующий вопрос:
При каком русском царе изучали математику в России по «Арифметике» Магницкого?
Все формулы мы с вами повторили.
Урок успешно завершили.
Литература
Ю.Н. Макарычев, Н.Г. Миндюк. К.И. Нешков, с. Б Суворова ; под ред. С.А. Теляковского. Алгебра. Учебник для 9 кл. общеобразовательных учреждений. Москва. «Просвещение» 2012 г.
Лысенко Ф. Ф. Алгебра 9кл. Итоговая аттестация. Ростов-на-Дону. Издательство «Легион» 2015.