Просмотр содержимого документа
«К семинару "Решение тригонометрических уравнений"»

СЕМИНАР 10 – 11 классы.
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

ЦЕЛЬ :
- Обобщение знаний по решению тригонометрических уравнений.
- Выделение основных проблем при решении этих уравнений:
- Потеря корней.
- Посторонние корни.
- Отбор корней.

ПЛАН УРОКА .
- Вводная часть, повторение теоретического материала. (Фронтальная работа)
- Решение тригонометрических уравнений. ( Групповая работа)
- Проблемы, возникающие при решении тригонометрических уравнений.

Основные методы решения
тригонометрических уравнений.
- Разложение на множители.
- Введение новой переменной.
- Функционально – графический метод.

Некоторые типы тригонометрических уравнений .
- Уравнения, сводящиеся к квадратным, относительно
cos х = t , sin х = t .
A sin 2 x + B cosx + C = 0
A cos 2 x + В sinx + C = 0
- A sin 2 x + B cosx + C = 0 A cos 2 x + В sinx + C = 0
- A sin 2 x + B cosx + C = 0 A cos 2 x + В sinx + C = 0
Решаются методом введения новой переменной.
2.Однородные уравнения первой и второй степени.
I ст . A sinx + B cosx = 0 : cosx
A tg x + B = 0
II ст . A sin 2 x + B sinx cosx + A cos 2 x = 0 : cos 2 x
A tg 2 x + B tgx + C = 0
Решаются методом разложения на множители и методом введения новой переменной .
3. Уравнение вида:
А sinx + B cosx = C . А, В, С 0
Применимы все методы.

4. Понижение степени.
А cos 2 x + В = C .
A cos2x + B = C.
Решаются методом разложения на множители.
A sin2x + B = C.
A sin2x + B = C.
Сводятся к однородным уравнениям С = С( ).
Сводятся к уравнению А sin 2 x + B cos 2 x = C .
5. Уравнение вида:
A(sinx + cosx) + B sin2x + C = 0.
Сводятся к квадратным относительно t = sinx + cosx .

Формулы .
Универсальная подстановка.
х + 2 n ; Проверка обязательна!
Понижение степени.
= (1 + cos2x ) : 2
= (1 – cos 2x) : 2
Метод вспомогательного аргумента.
a cosx + b sinx заменим на C sin ( x + ), где
cos =
sin =
- вспомогательный аргумент.

Правила .
- Увидел квадрат – понижай степень.
- Увидел произведение – делай сумму.
- Увидел сумму – делай произведение.

Потеря корней, лишние корни.
1.Потеря корней:
- делим на g (х).
- опасные формулы (универсальная подстановка).
Этими операциями мы сужаем область определения.
2. Лишние корни:
- возводим в четную степень.
- умножаем на g (х) (избавляемся от знаменателя).
Этими операциями мы расширяем область определения.
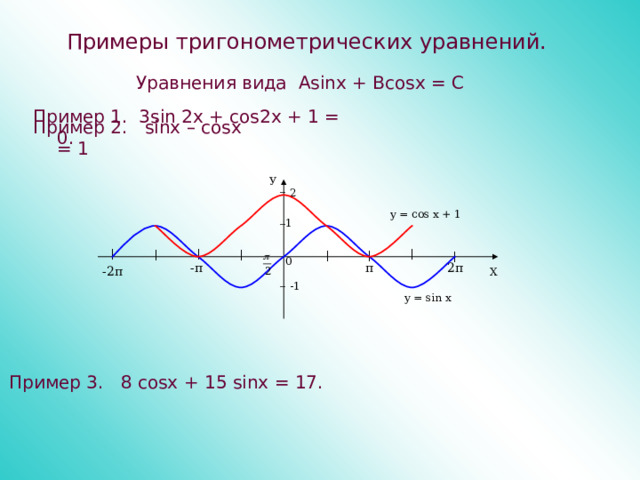
Примеры тригонометрических уравнений.
Уравнения вида Asinx + Bcosx = C
Пример 1. 3 sin 2 x + cos 2 x + 1 = 0.
Пример 2. sinx – cosx = 1
У
_
2
y = cos x + 1
_
1
|
|
|
|
|
|
|
|
0
-π
2π
π
-2π
Х
_
-1
y = sin x
Пример 3. 8 cosx + 15 sinx = 17.

Понижение степени.
Уравнения вида A cos 2 x + B = C . A cos2x + B = C.
Пример.
Сведение к однородному.
A sin2x + B sin 2 x = C, Asin2x + Bcos 2 x = C.
Уравнения вида
Пример. 5 sin 2 x +
sinx cosx + 6 cos 2 x = 5.
Уравнение вида: А( sinx + cosx ) + В sin 2 x + С = 0.
Пример. 4 + 2 sin 2 x – 5( sinx + cosx ) = 0.
Разложение на множители.
Пример. - 2 cosx = 4 sinx - sin 2 x

Проблемы, возникающие при решении тригонометрических уравнений.
1.Потеря корней .
- Делим на g (х).
- Применяем опасные формулы.
Пример. cos x = sin x * sin
2. Посторонние корни.
- Освобождаемся от знаменателя.
- Возводим в четную степень.

Пример 1 .
(sin 4x – sin 2x + cos 3x + 2sin x – 1) : (2sin 2x - ) = 0
У
/
/
\
π
2π
Х
\
Пример 2.
У
/
\
π
2π
t

Отбор корней.
Пример.
tg x + tg 2 x = tg 3 x
.
х
0
х
0

































