СЕМИНАР ДЛЯ 10 – 11 КЛАССОВ ПО ТЕМЕ РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
ЦЕЛЬ: Обобщение знаний по решению тригонометрических уравнений всех типов.
Выделение основных проблем при решении этих уравнений:
потеря корней.
посторонние корни.
отбор корней.
ПЛАН УРОКА.
Вводная часть, повторение теоретического материала. (Фронтальная работа)
Решение тригонометрических уравнений. (Групповая работа)
Проблемы, возникающие при решении тригонометрических уравнений.
I. Вводная часть.
1.Основные методы решения тригонометрических уравнений.
Разложение на множители.
Введение новой переменной.
Функционально – графический метод.
2.Некоторые типы тригонометрических уравнений.
1.Уравнения, сводящиеся к квадратным, относительно cos х = t, sin х = t.
A sin
2 x + B cosx + C = 0 A cos
2 x + В sinx + C = 0
Решаются методом введения новой переменной.
2.Однородные уравнения первой и второй степени.
I

ст. A sinx + B cosx = 0 : cosx A tg x + B = 0 II ст. A sin
2 x + B sinx cosx
+
A cos
2 x = 0 : cos
2x A tg
2 x + B tgx + C = 0
Решаются методом разложения на множители и методом введения новой переменной.
3. Уравнение вида:
А

sinx + B cosx = C. А, В, С 0
Применимы все методы.
4. Понижение степени.
А cos2x + В cos
2x = C. A cos2x + B sin
2x = C.
Решаются методом разложения на множители.
A sin2x + B sin
2x = C. A sin2x + B cos
2x = C.
Сводятся к однородным уравнениям С = С(sin2х + cos2х).
Сводятся к уравнению А sin2x + B cos2x = C.
5. Уравнение вида:
A(sinx + cosx) + B sin2x + C = 0.
Сводятся к квадратным относительно t = sinx + cosx.
sin2x = t2 – 1.
3. Формулы.
Универсальная подстановка.
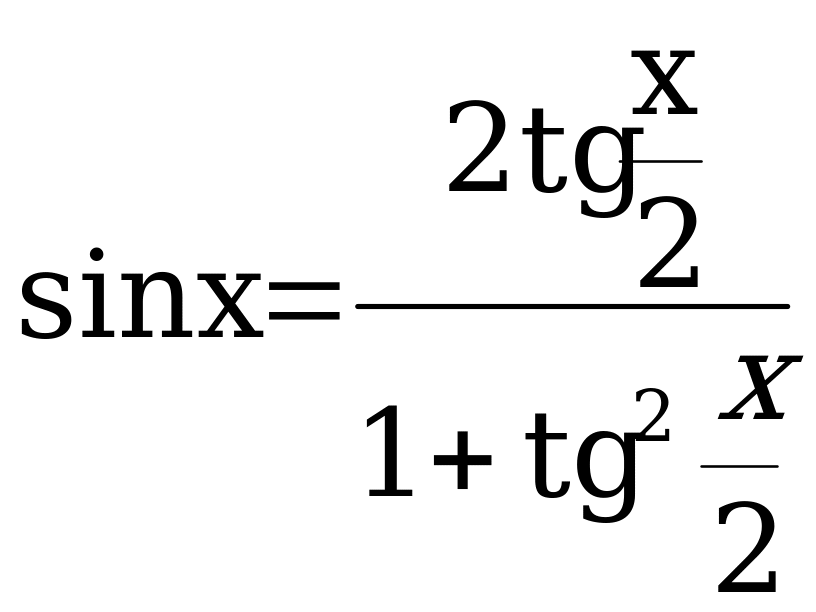
;
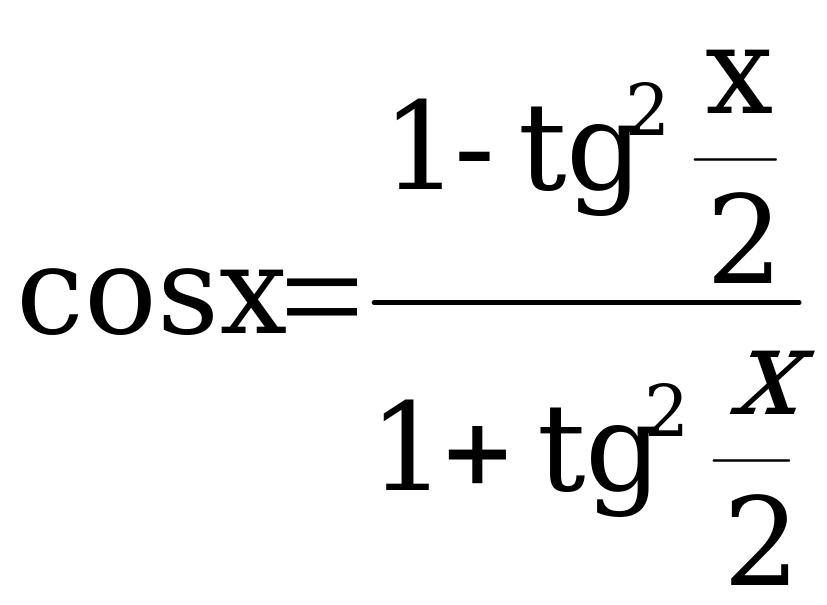
;
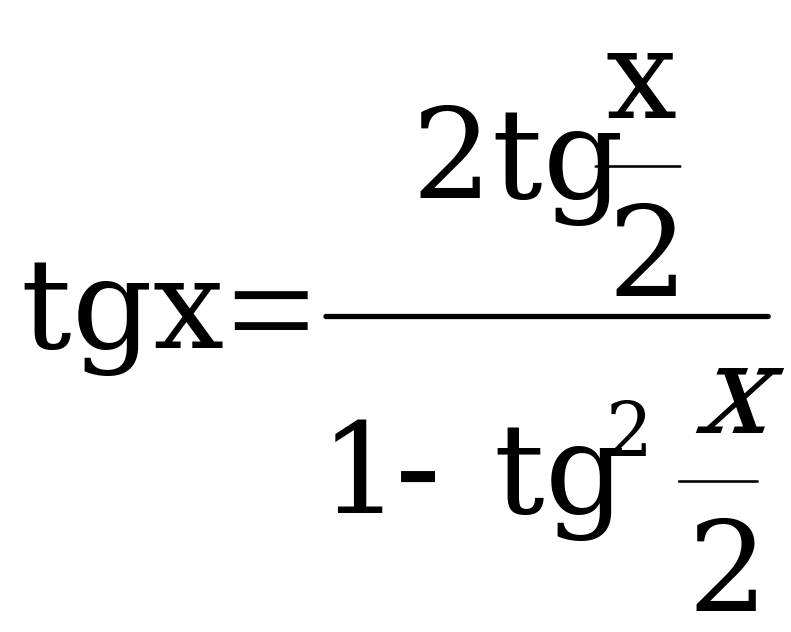
.
х + 2n; Проверка обязательна!
Понижение степени.
cos
2x = (1 + cos2x ) : 2 sin
2x = (1 – cos 2x) : 2
Метод вспомогательного аргумента.
a cosx +b sinx заменим на C sin(x+), где
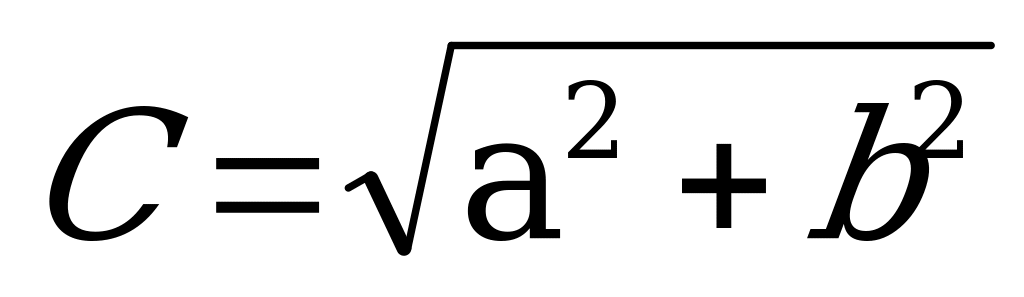
, sin =
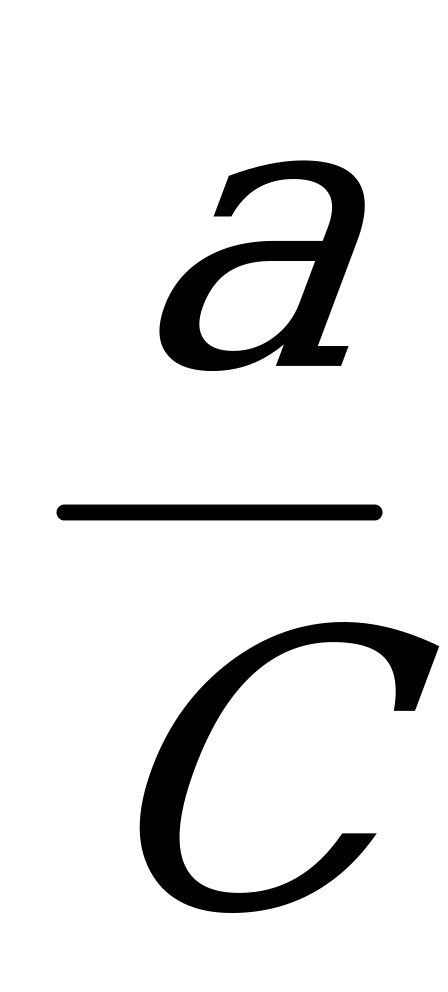
; cos =
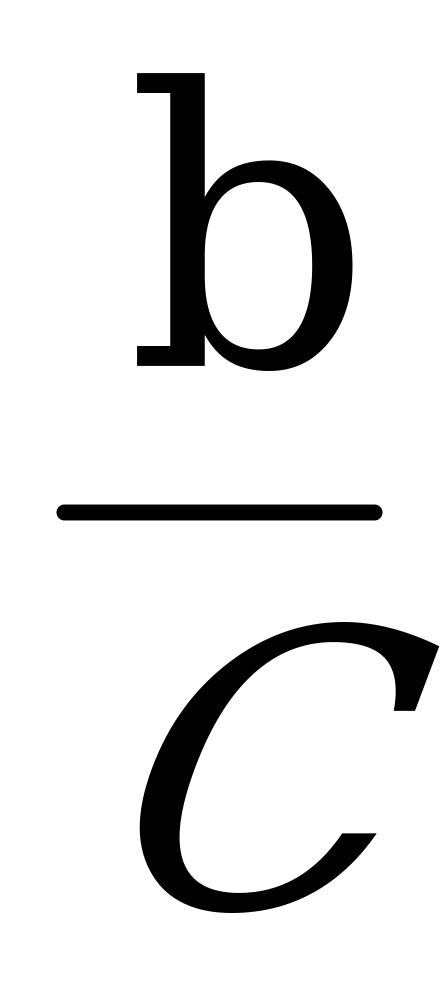
; - вспомогательный аргумент.
4. Правила.
Увидел квадрат – понижай степень.
Увидел произведение – делай сумму.
Увидел сумму – делай произведение.
5. Потеря корней, лишние корни.
1.Потеря корней:
Этими операциями мы сужаем область определения.
2. Лишние корни:
Возводим в четную степень.
Умножаем на g(х) (избавляемся от знаменателя).
Этими операциями мы расширяем область определения.
II. Примеры тригонометрических уравнений.
1. Уравнения вида Asinx + Bcosx = C
Решение.
Воспользуемся универсальной подстановкой:
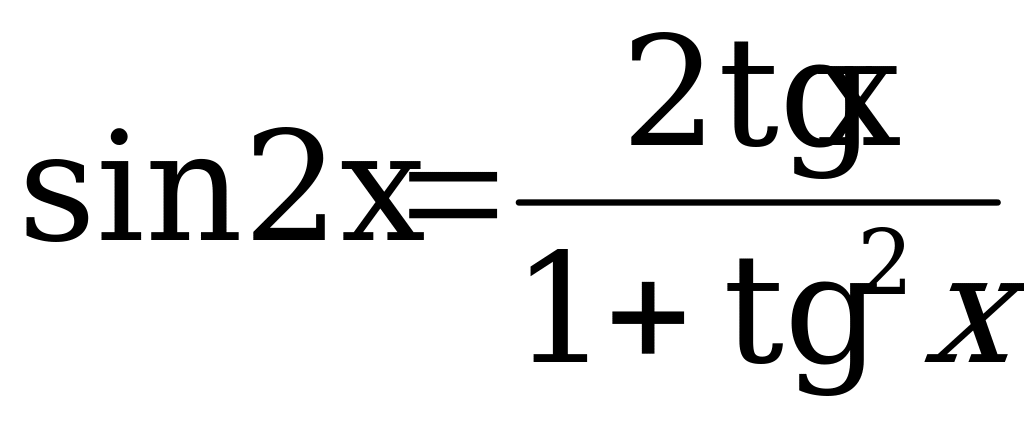 ,
, 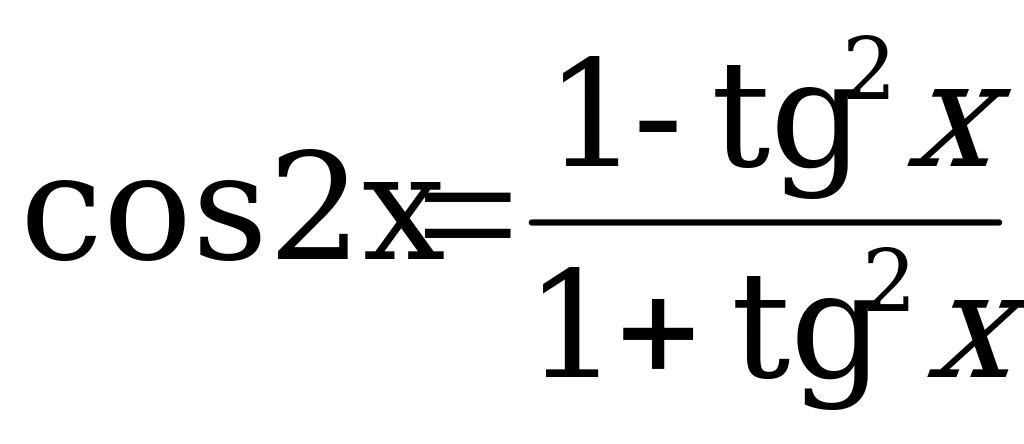
Положим tgx = u. где x  + n, тогда sin2x =
+ n, тогда sin2x = 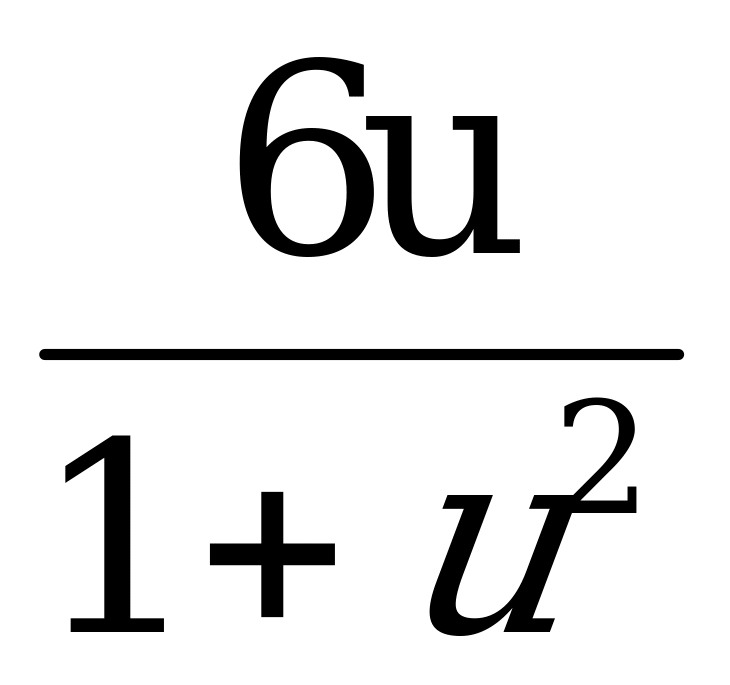 , cos2x =
, cos2x =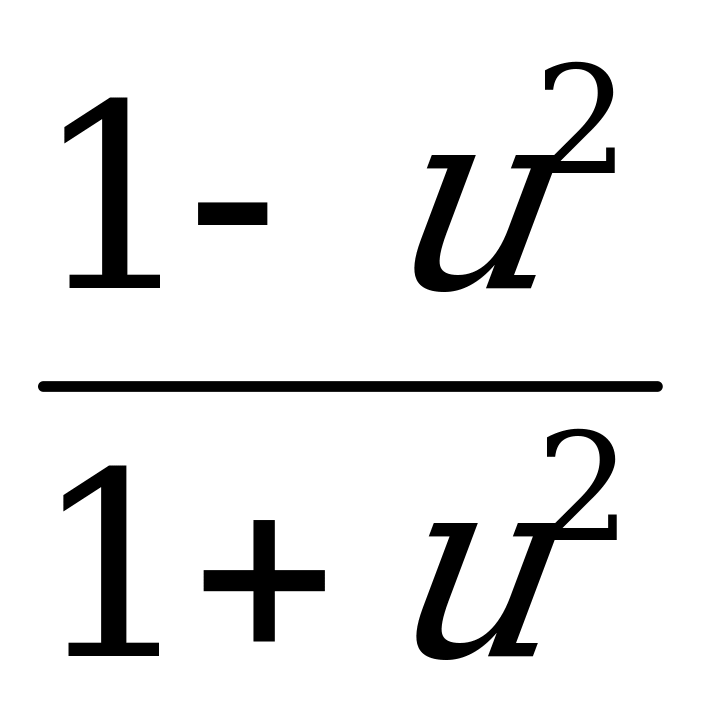 .
.
Уравнение примет вид 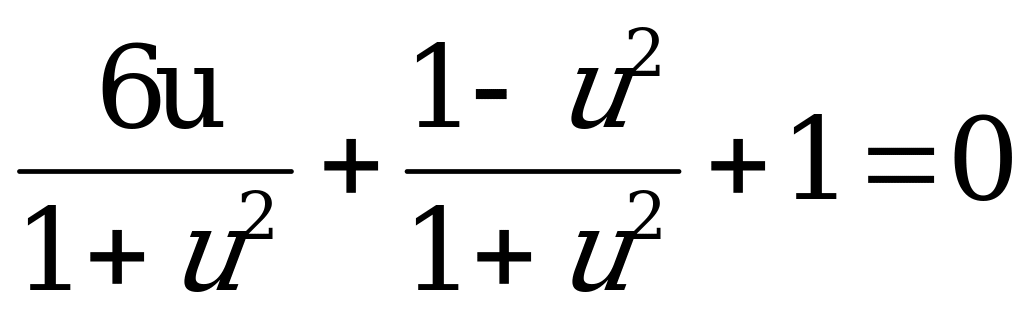
Решив это уравнение, получим u =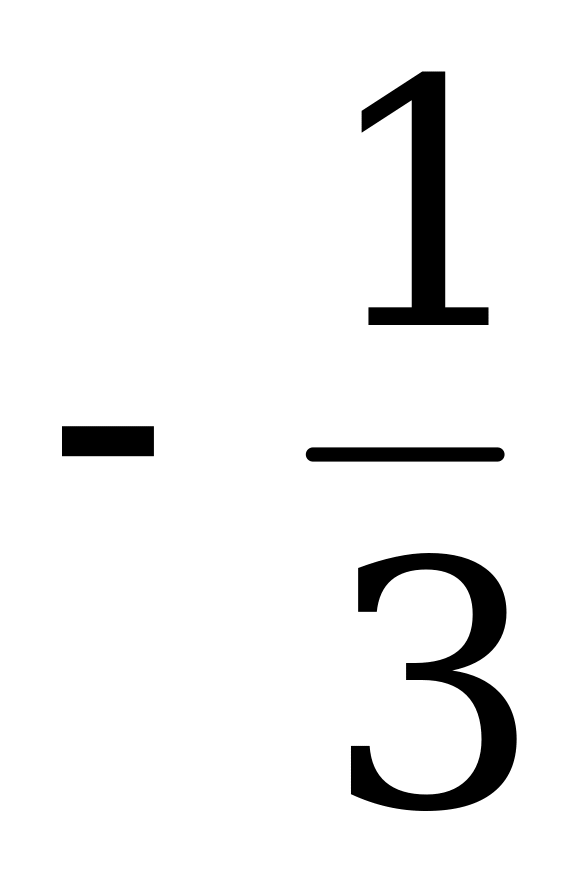
Таким образом, tg x =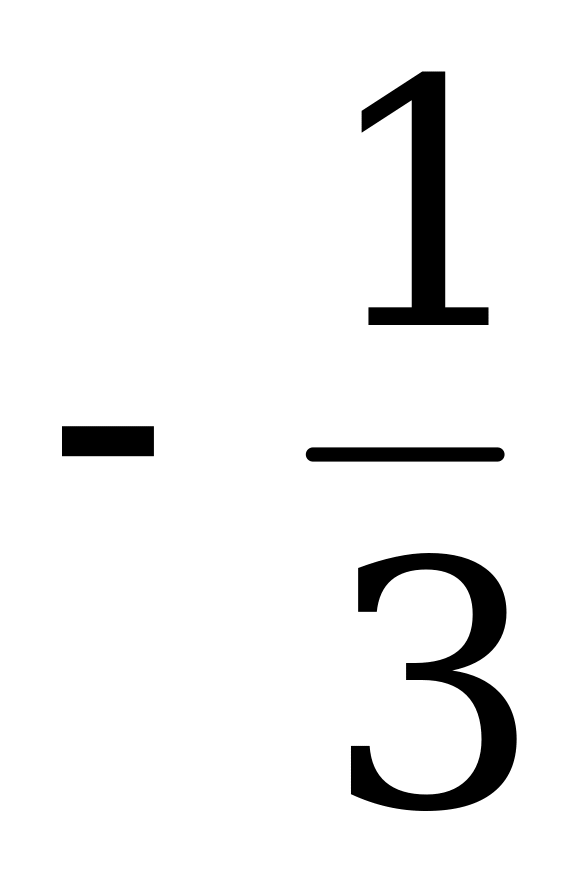 , откуда x = arctg(
, откуда x = arctg(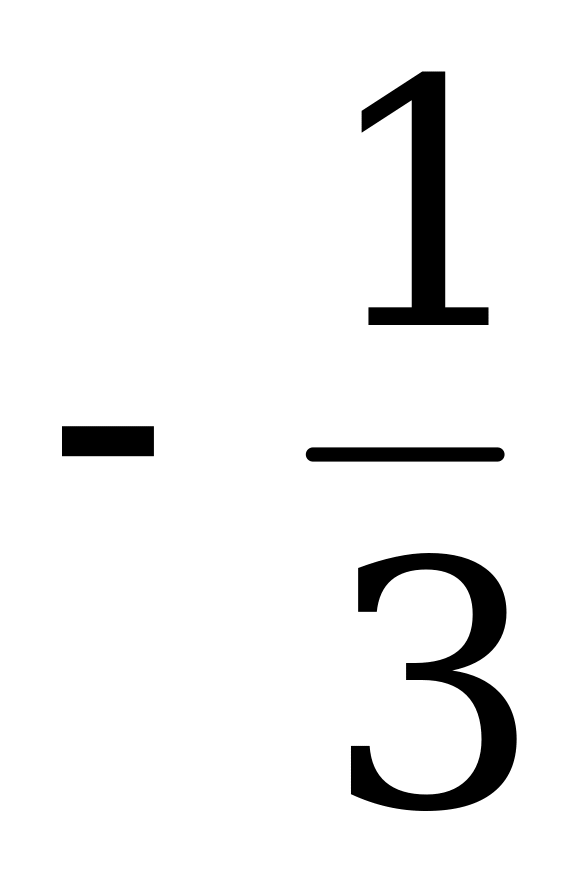 ) + k, k Z.
) + k, k Z.
Проверим отброшенные корни x  + n.
+ n.
Проверка:
3 sin( + 2n) + cos( + 2n) + 1 = 3 sin + cos + 1 = 0 – 1 + 1 = 0.
Т.е. x =  + n, n Z, являются корнями уравнения.
+ n, n Z, являются корнями уравнения.
Ответ: х = arctg(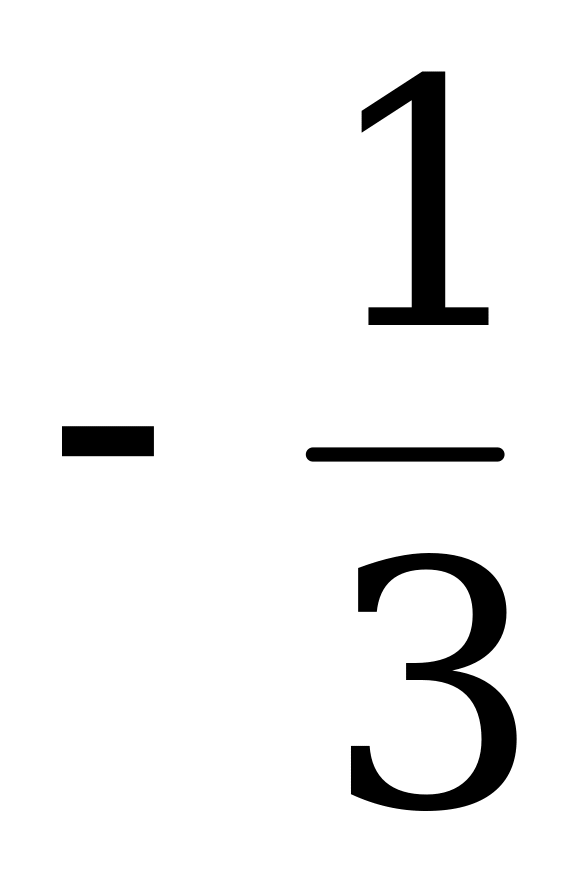 ) + k, k Z, x =
) + k, k Z, x =  + n, n Z.
+ n, n Z.
Решение.
В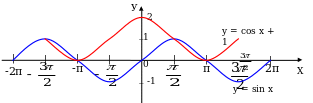 оспользуемся функционально-графическим методом.
оспользуемся функционально-графическим методом.
Преобразуем уравнение к виду sinx = cosx + 1. Построим графики функций y= sinx, y=cosx+1
Ответ: х =  + 2 n, n ; x = + 2 k, k Z.
+ 2 n, n ; x = + 2 k, k Z.
Решение.
Воспользуемся введением вспомогательного аргумента.
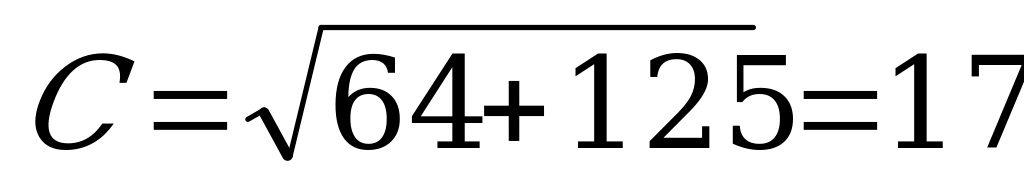 ,
,
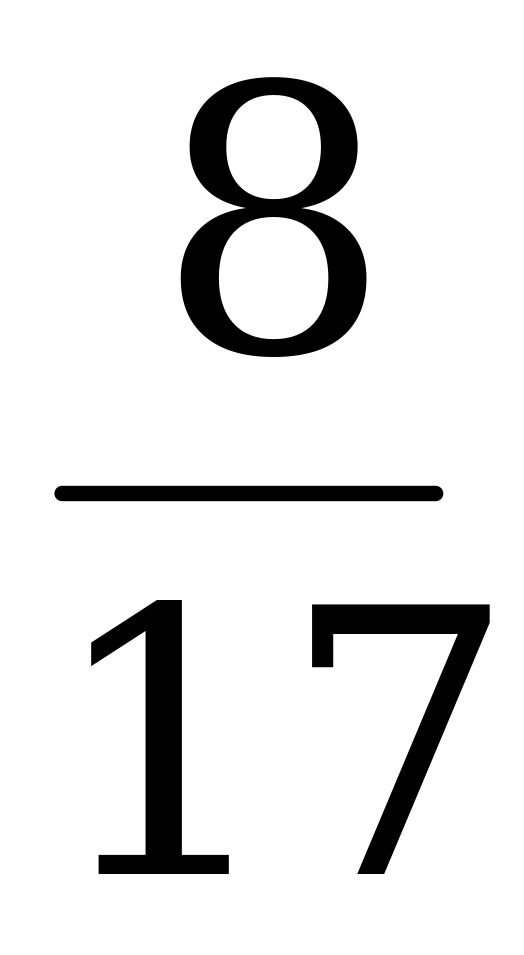 cosx +
cosx + 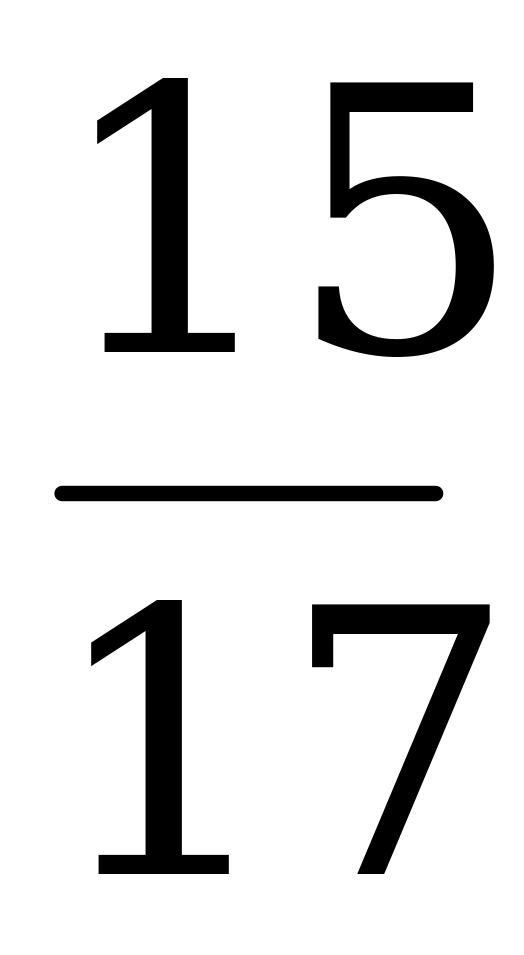 sinx = 1, т.к.
sinx = 1, т.к. 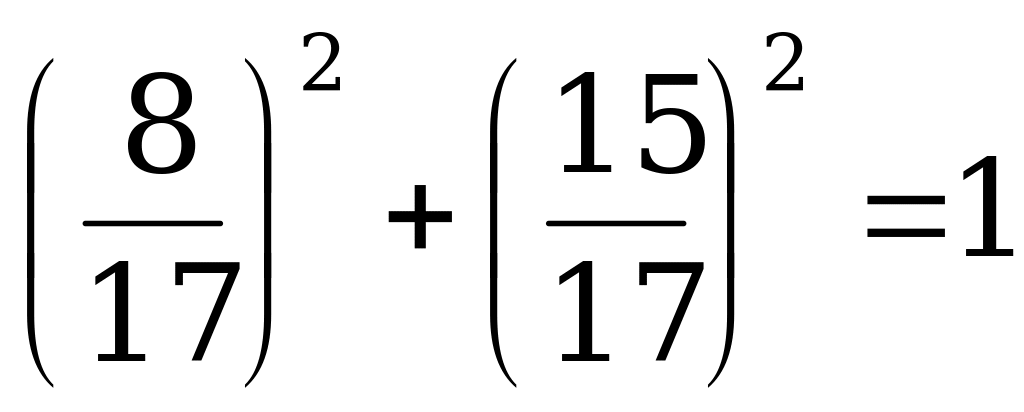 , то существует такое ,
, то существует такое ,
что sinj = 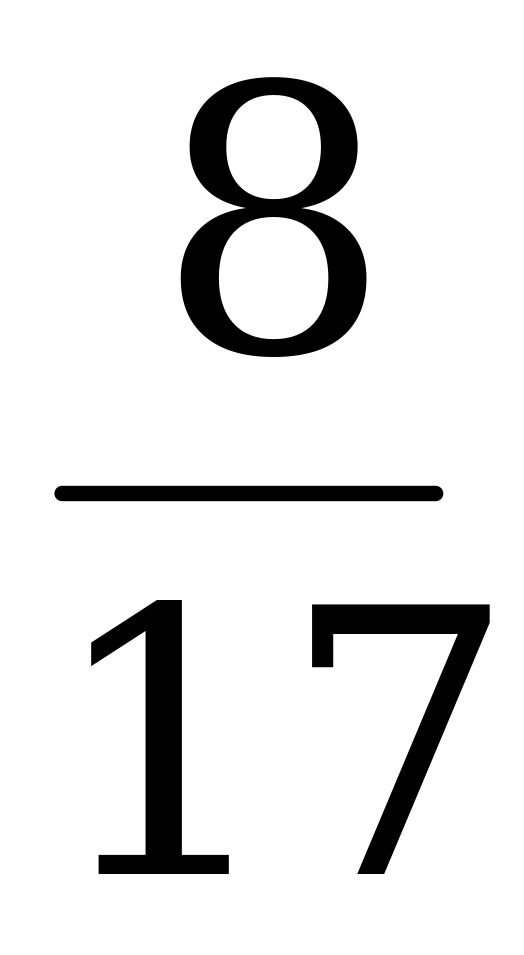 , cosj =
, cosj = 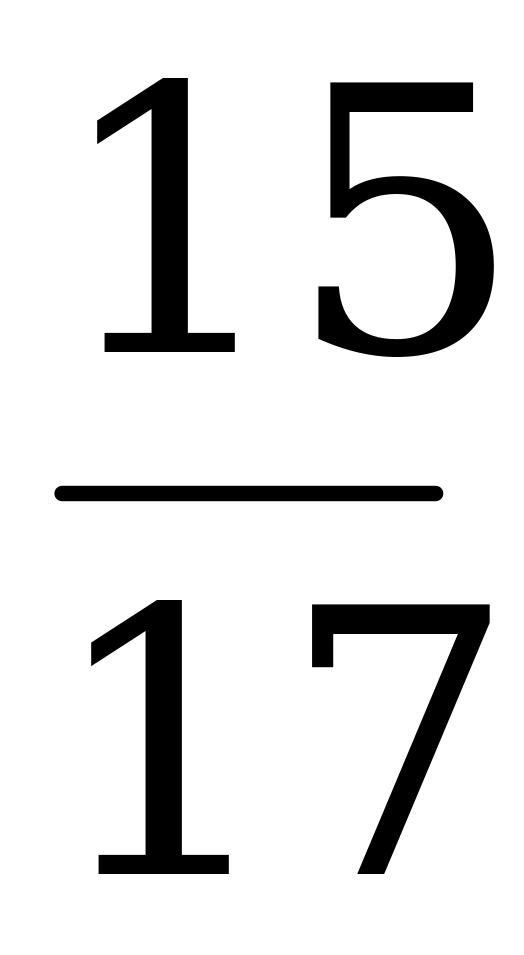 , значит sinj cosx + sinx cosj = 1; j = arcsin
, значит sinj cosx + sinx cosj = 1; j = arcsin 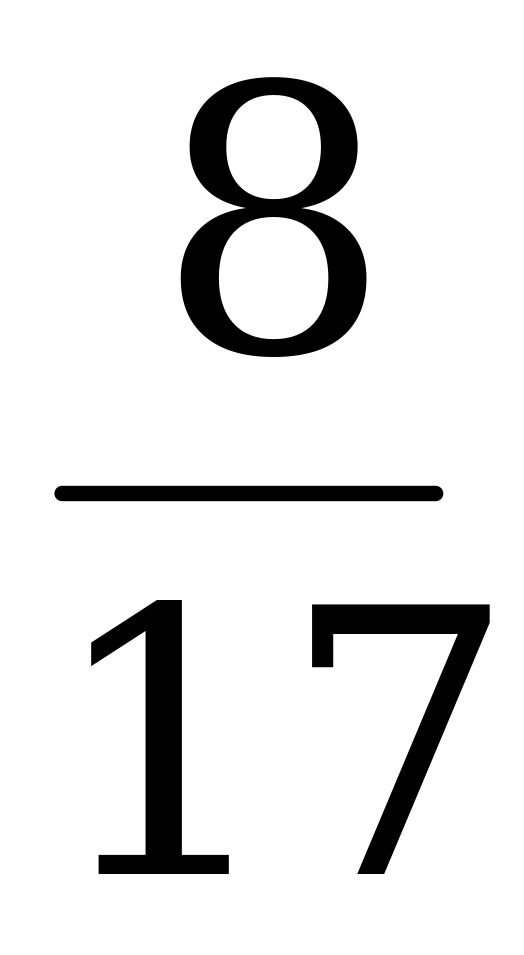 .
.
sin(x + j) = 1, x + j = + 2n, x =
+ 2n, x =  + 2n - j.
+ 2n - j.
Ответ: x =  + 2n - j, x =
+ 2n - j, x =  + 2pn – arcsin
+ 2pn – arcsin 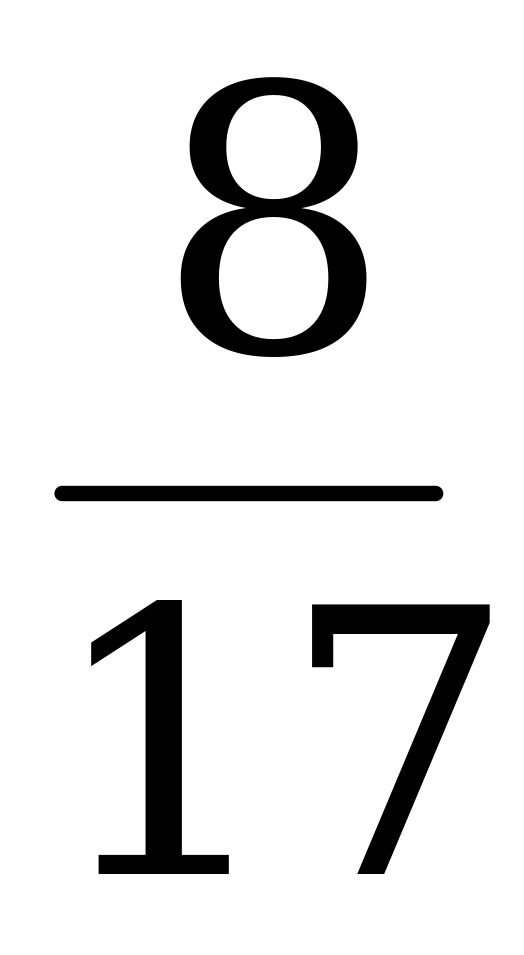 , n Z.
, n Z.
2. Понижение порядка.
Уравнения вида A cos2x + B sin2x = C. A cos2x + B cos2x = C.
Решение.
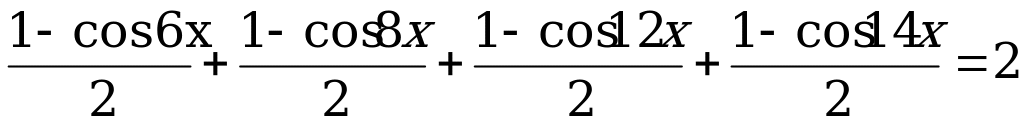
1 – cos 6x + 1 – cos 8x + 1 – cos 12x + 1 – cos 14x = 4
cos 6x + cos 8x + cos 12x + cos 14x = 0, 2cos10x cos 4x + 2cos 10x cos 2x = 0,
2cos 10x(cos 4x + cos 2x) = 0, 2cos10x 2cos3x cosx = 0,
cos10x = 0, cos3x = 0, cosx = 0.
Ответ: х = 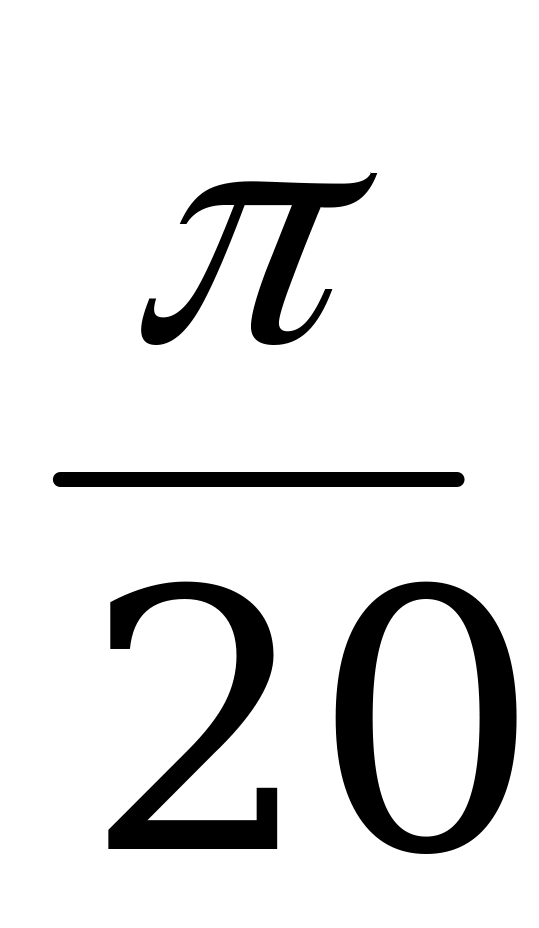 +
+ 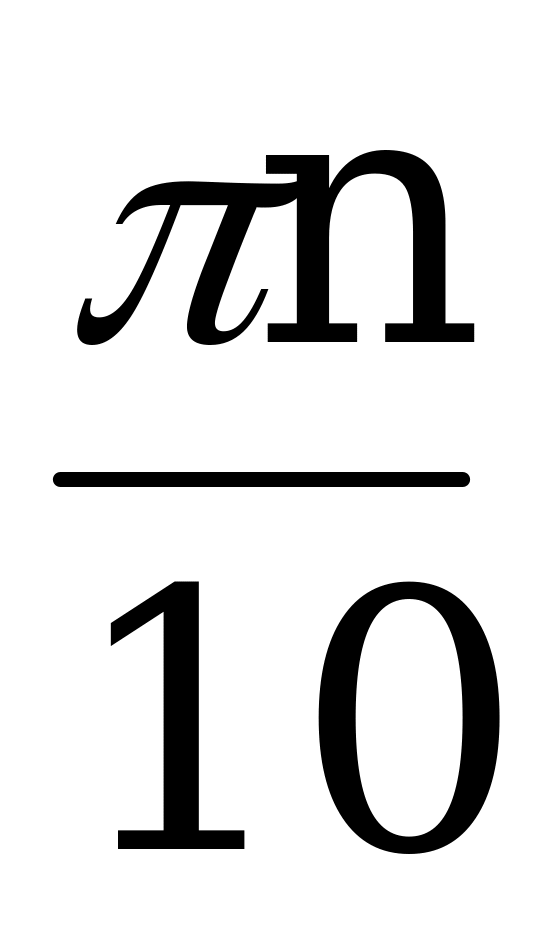 , n Z; x =
, n Z; x = 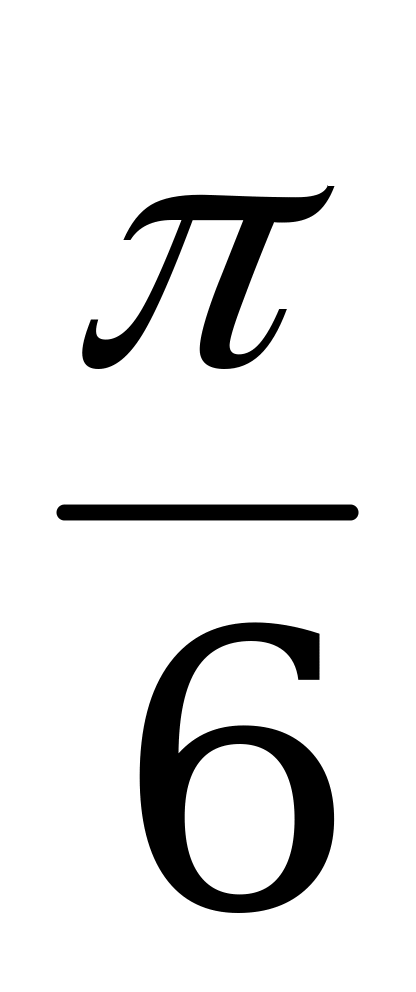 +
+ 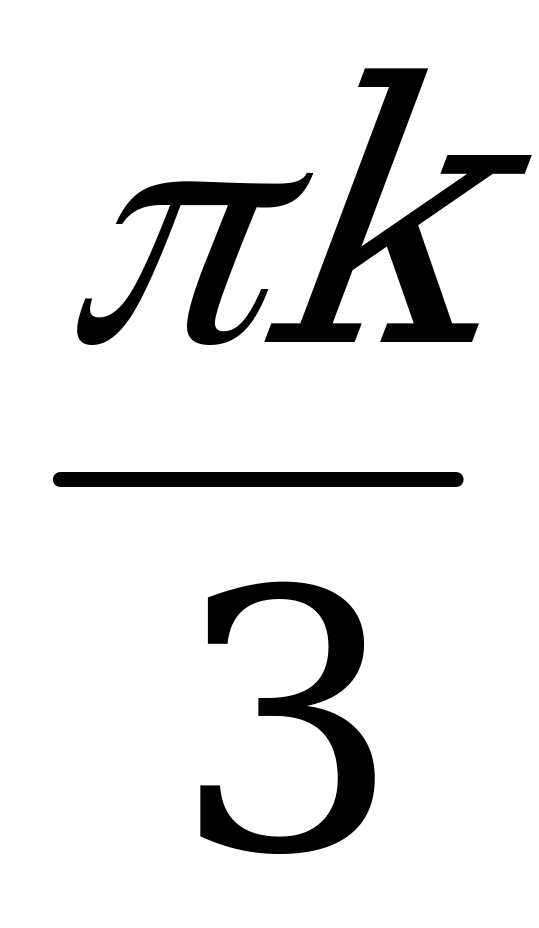 , k Z; x =
, k Z; x =  + pm, m Z.
+ pm, m Z.
при k = 1 и m = 0 серии совпадают.
k = 4 и m = 1.
3. Сведение к однордному.
Уравнения вида A sin2x + B sin2 x = C, Asin2x + Bcos2 x = C.
Решение.
5 sin2 х + 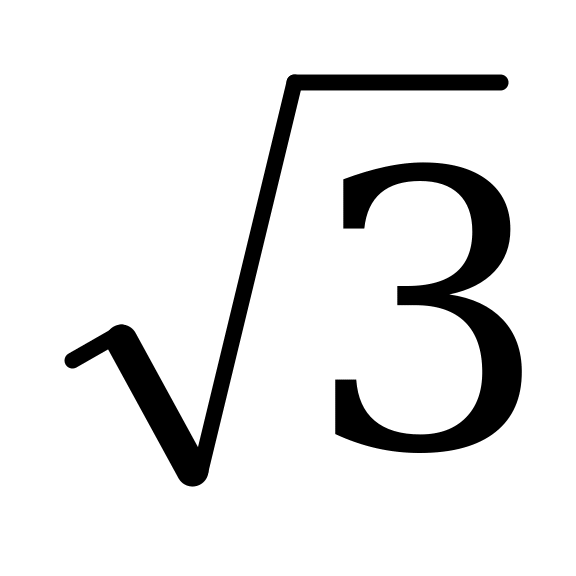 sinx cosx + 6cos2 х – 5 sin2 х – 5 cos2 х = 0
sinx cosx + 6cos2 х – 5 sin2 х – 5 cos2 х = 0
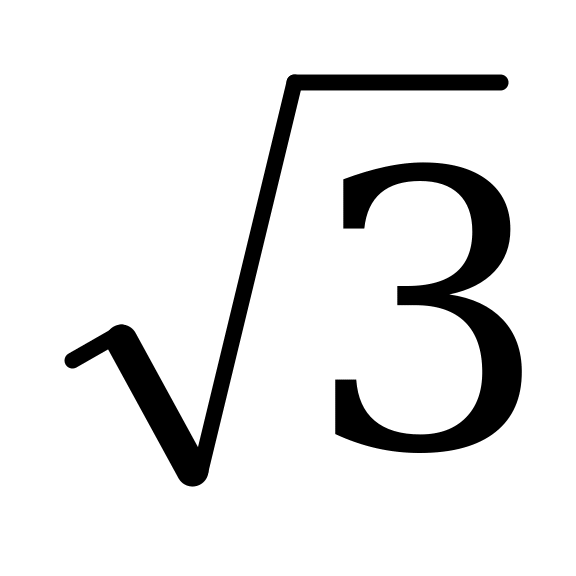 sinx cosx + cos2х = 0 разложим на множители
sinx cosx + cos2х = 0 разложим на множители
cosx (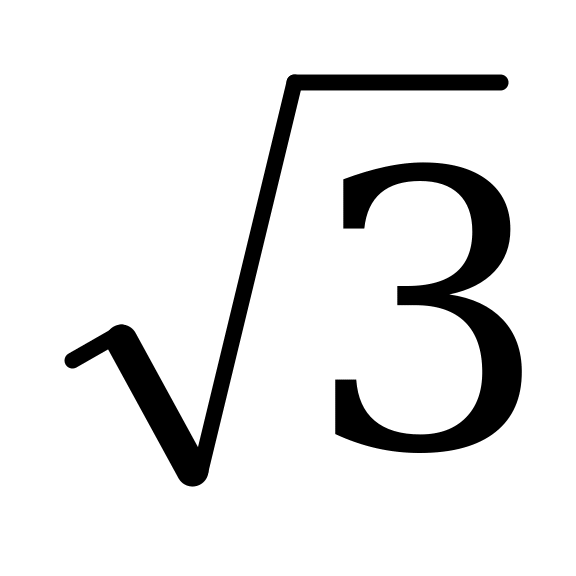 sinx + cosx ) = 0, откуда 1. cosx = 0, 2.
sinx + cosx ) = 0, откуда 1. cosx = 0, 2. 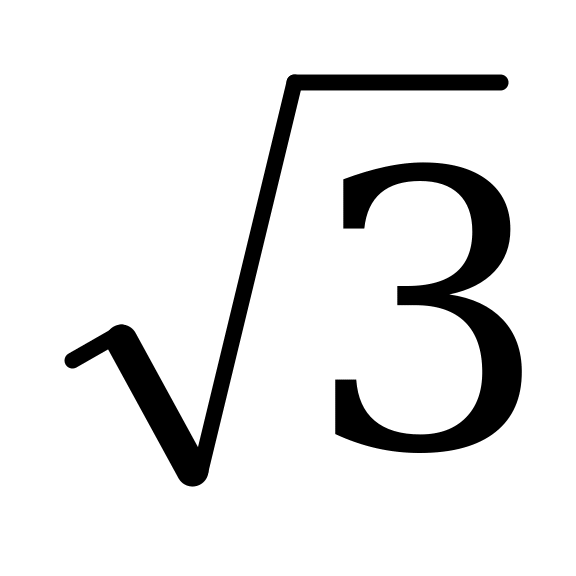 sinx + cosx = 0.
sinx + cosx = 0.
х =  + pk, k Z. tgx =
+ pk, k Z. tgx = 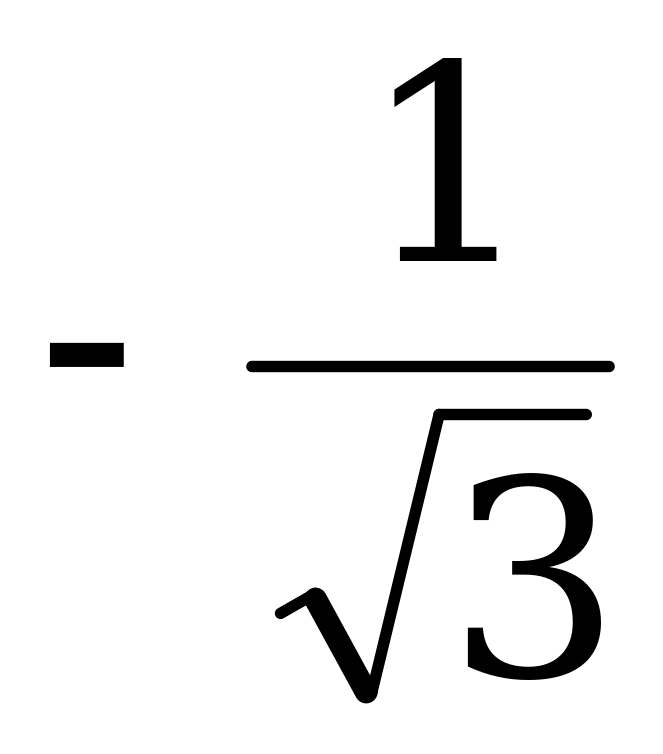 ,
,
x = 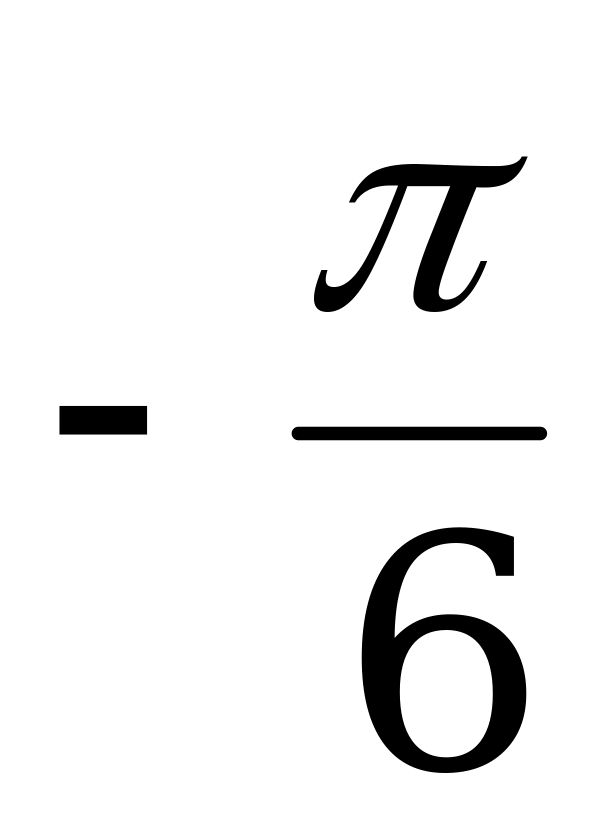 + pn, n Z.
+ pn, n Z.
Ответ: х = + pk, k Z. x =
+ pk, k Z. x = 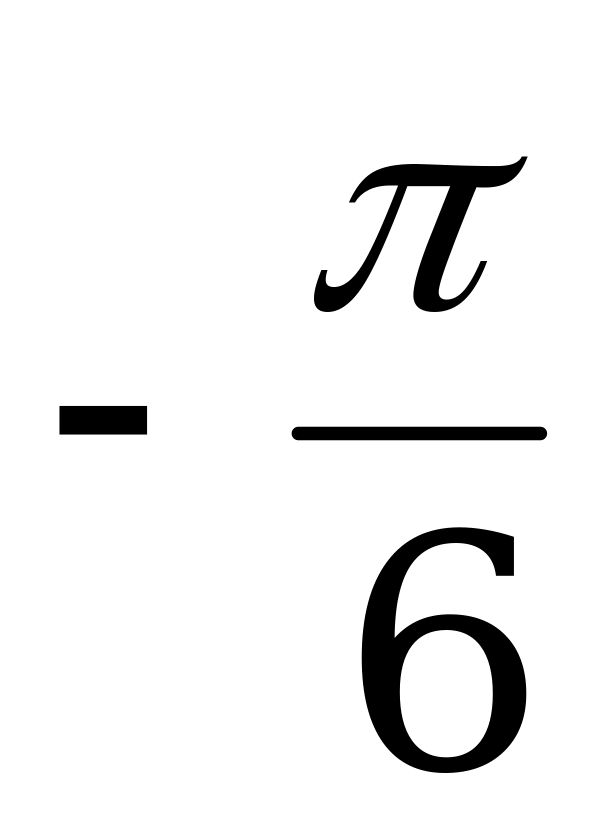 + pn, n Z
+ pn, n Z
4. Уравнение вида: А(sinx + cosx) + В sin2x + С = 0.
Решение.
sinx + cosx = t, sin2x = t2 – 1.
4 + 2t2 – 2 – 5t = 0, t 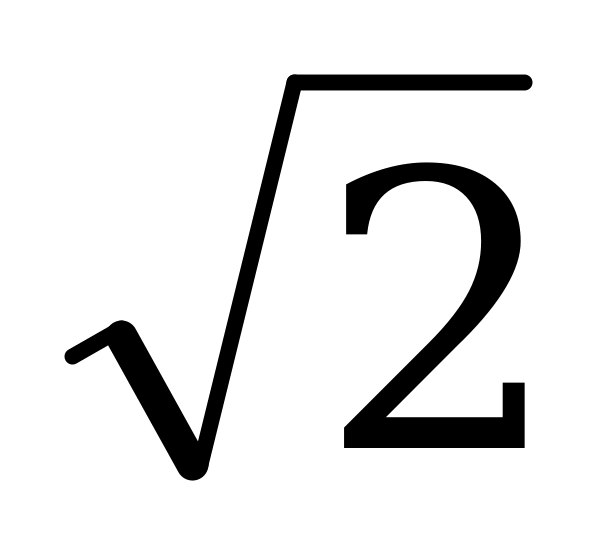
2 t2 – 5t + 2 = 0. t1 = 2, t2 = 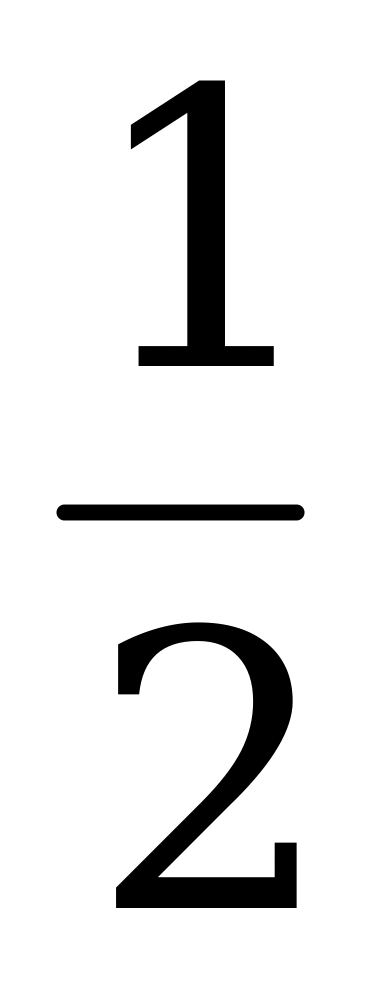
sinx + cosx = 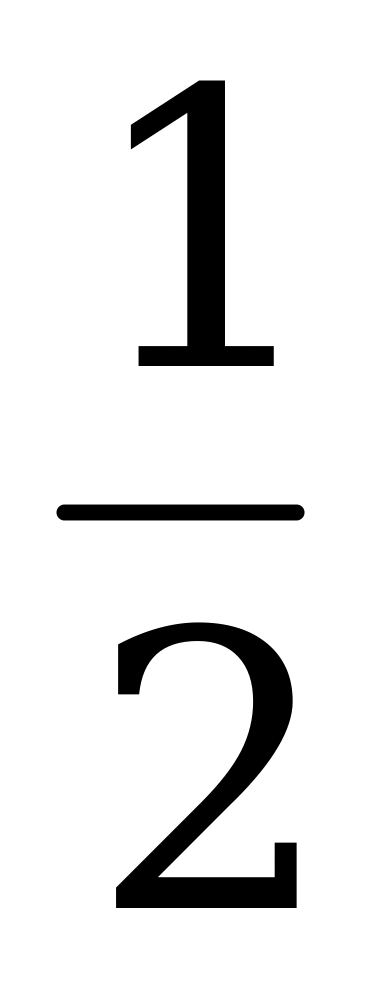 , заменим cosx = sin(x +
, заменим cosx = sin(x +  ),
),
sinx + sin(x +  ) =
) = 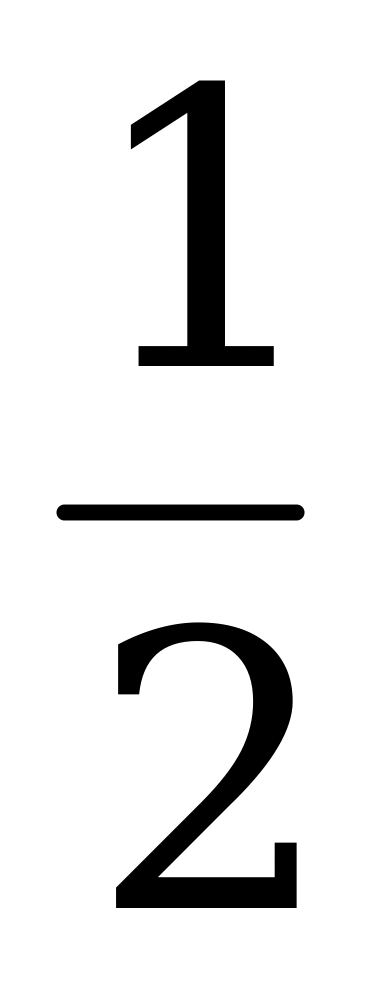 , 2sin(x +
, 2sin(x + 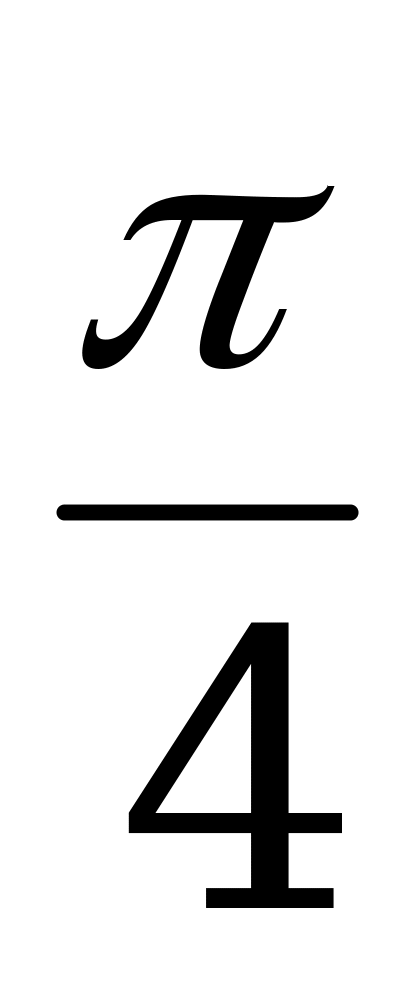 ) cos(
) cos(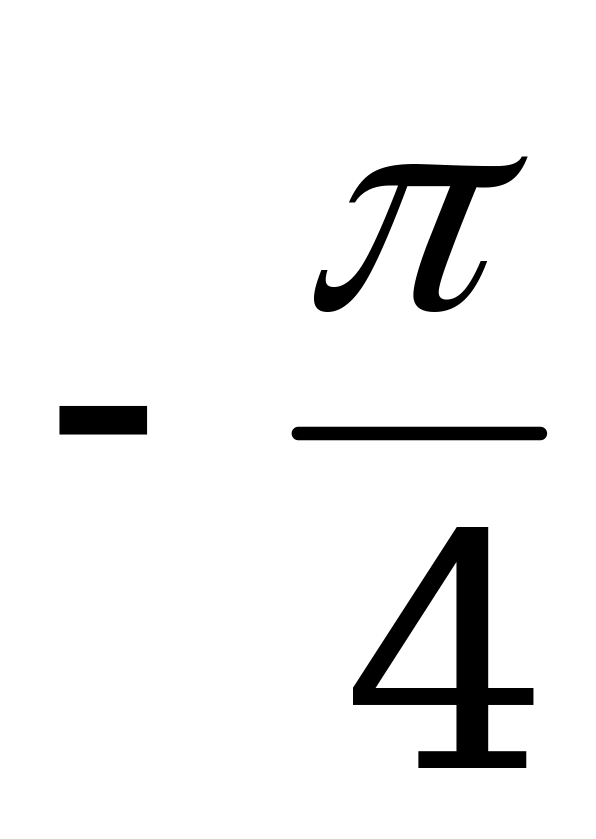 ) =
) = 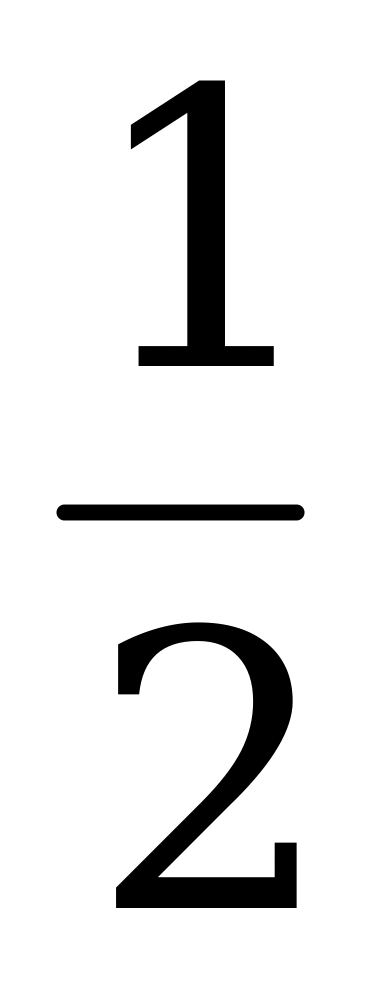 ,
,
sin(x + 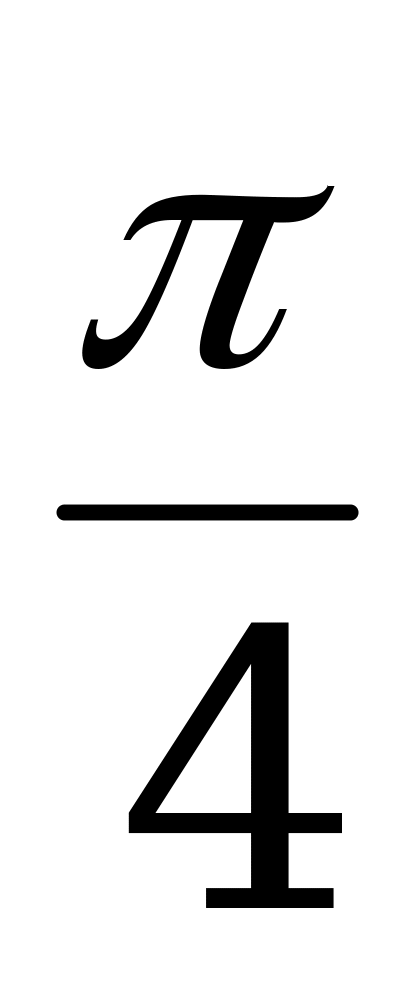 ) =
) = 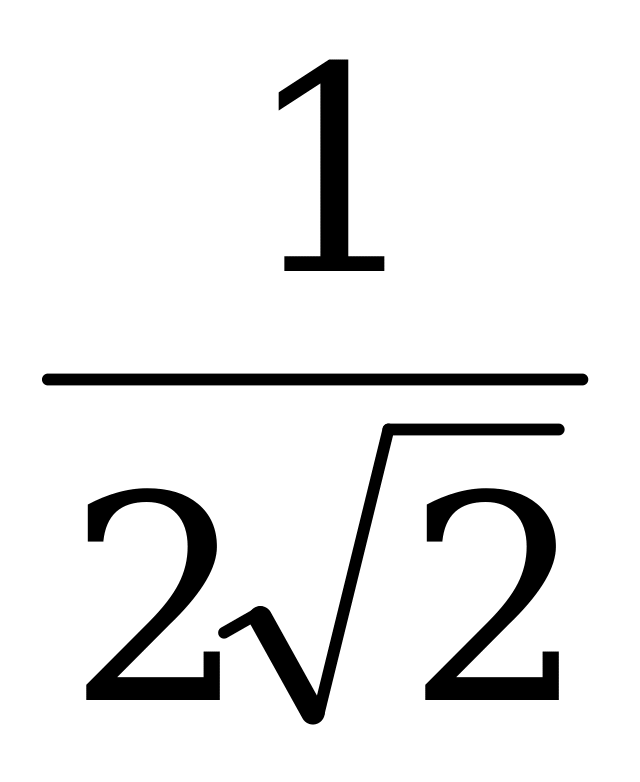 ; x +
; x + 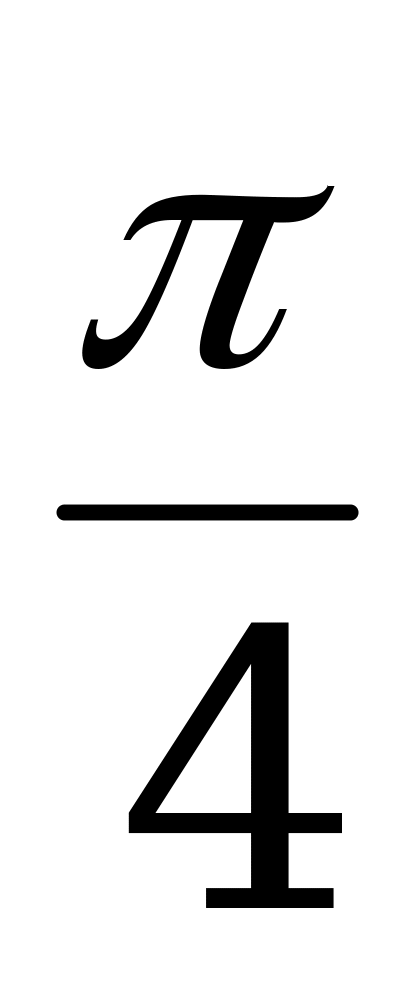 = (-1)karcsin(
= (-1)karcsin(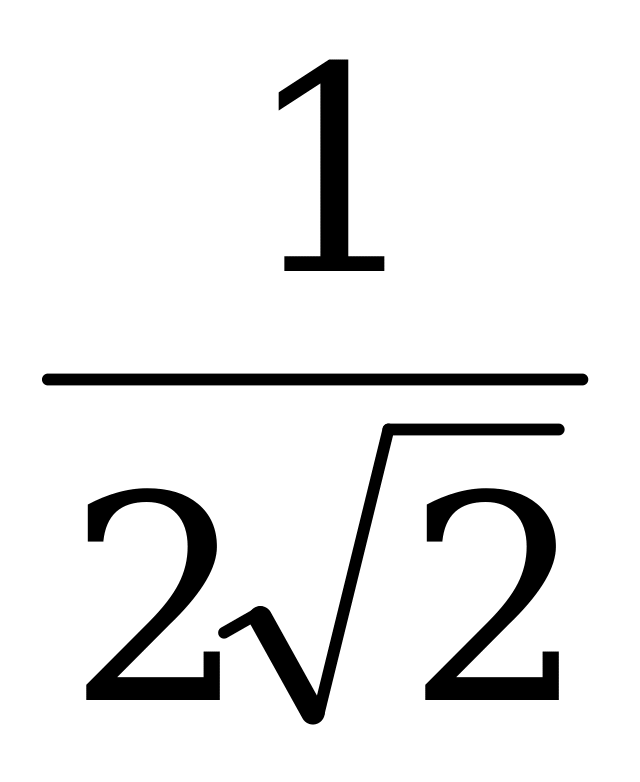 ) + pk, k Z.
) + pk, k Z.
Ответ: х = (-1)karcsin(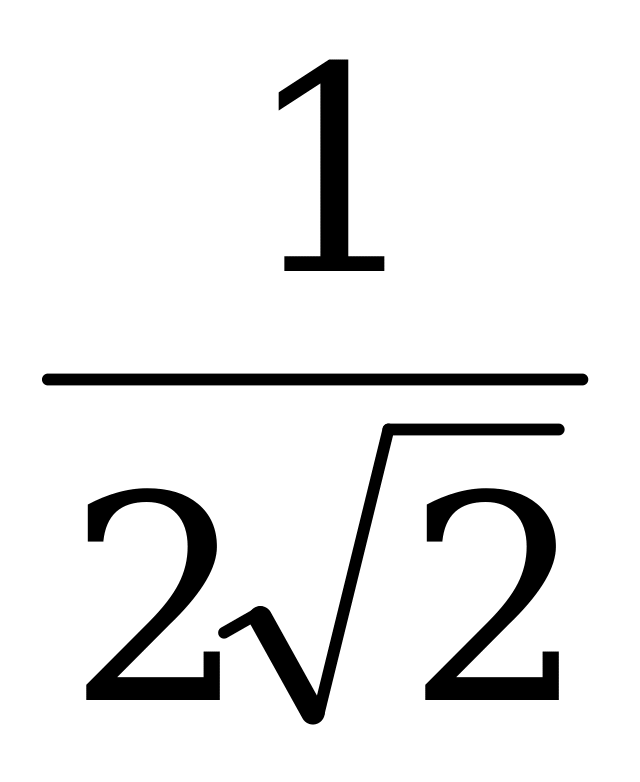 ) -
) - 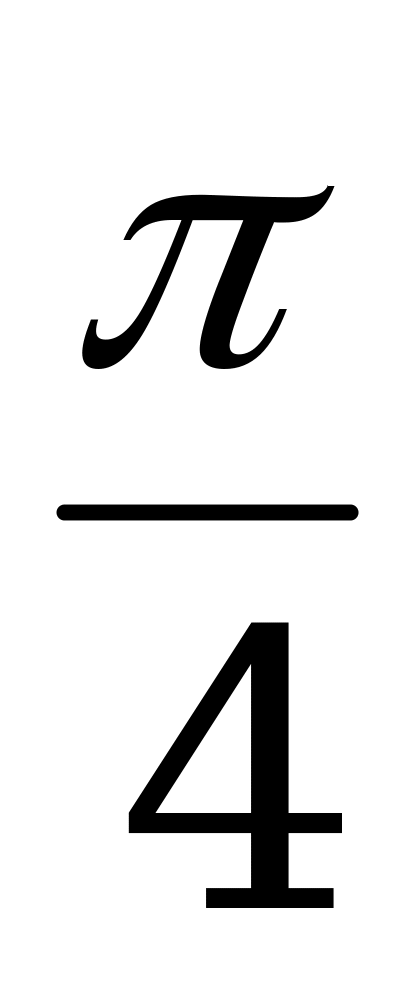 + pk, k Z.
+ pk, k Z.
5. Разложение на множители.
Решение.
cosx(cosx –2) = 2 sinx (2 – cosx),
(cosx – 2)(cosx + 2 sinx) = 0.
1). сosx = 2, 2). сosx +2 sinx = 0
корней нет. 2tgx + 1 = 0
x = arctg(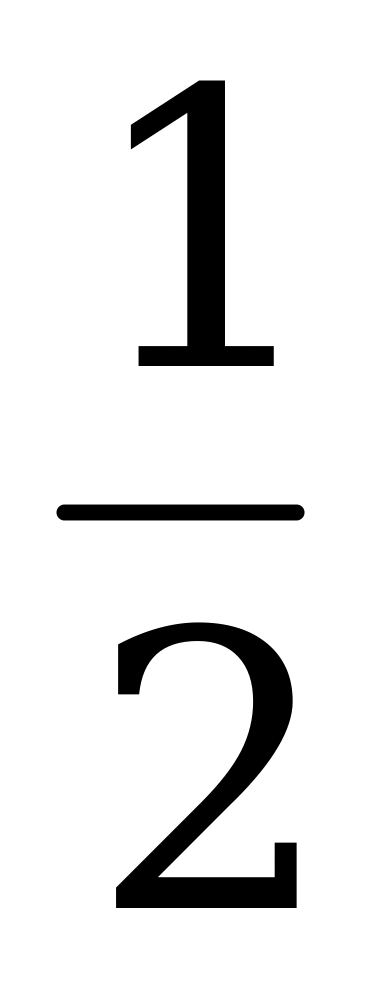 ) + pn, n Z.
) + pn, n Z.
Ответ: x = arctg(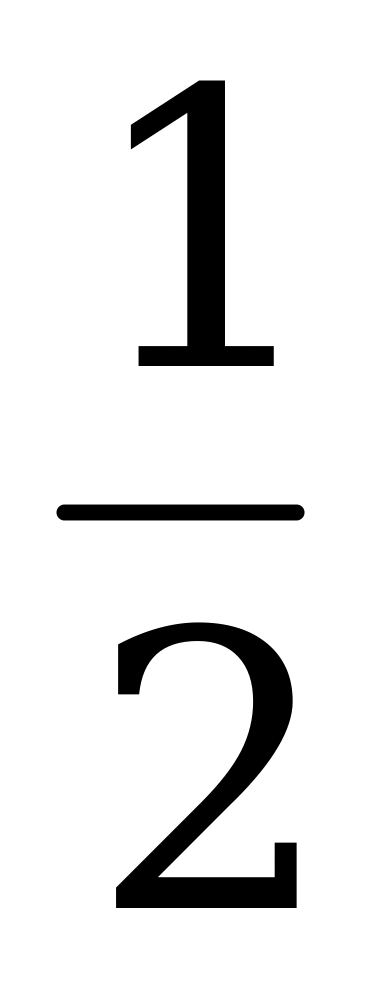 ) + pn, n Z.
) + pn, n Z.
III. Проблемы, возникающие при решении тригонометрических уравнений.
1.Потеря корней.
Найдите ошибку.
1 - сosx = sinx* sin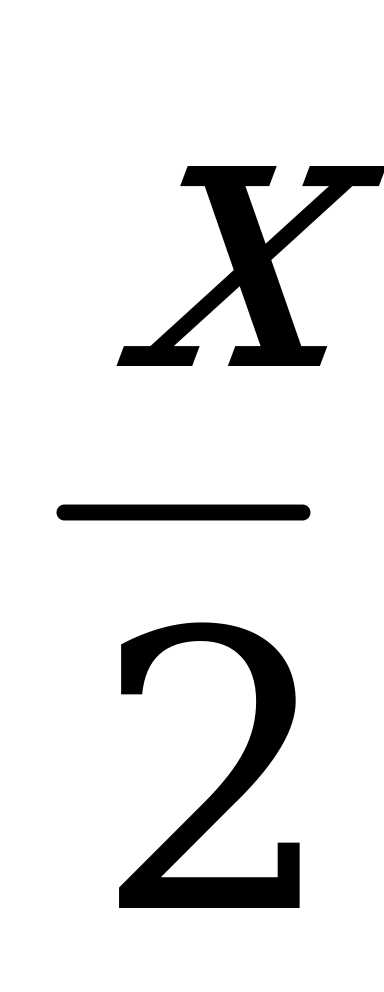 ,
,
Решение.
Заменим левую часть уравнения по формуле 1 - сosx = 2sin2 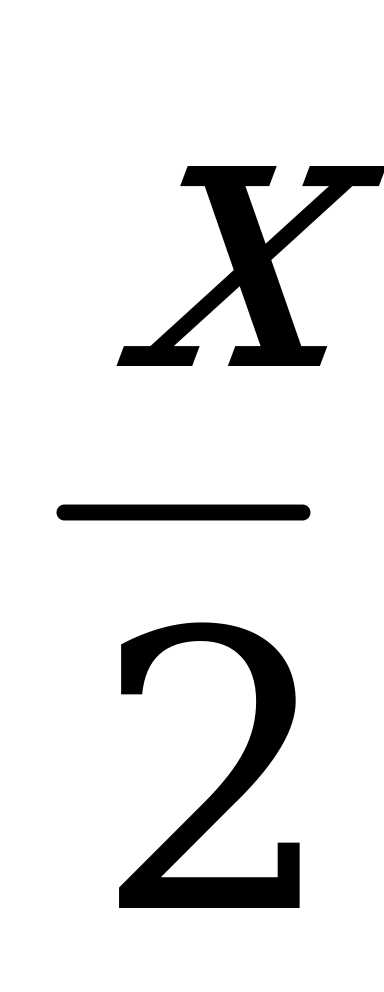 ,
,
а правую часть уравнения по формуле sinx = 2sin 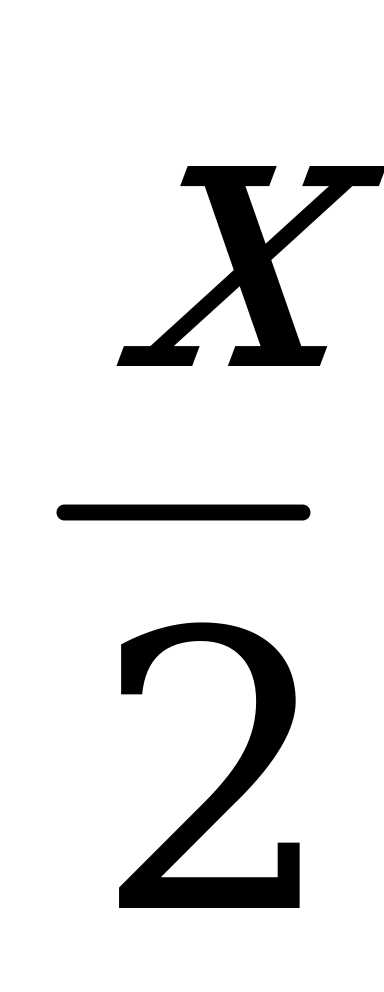 *cos
*cos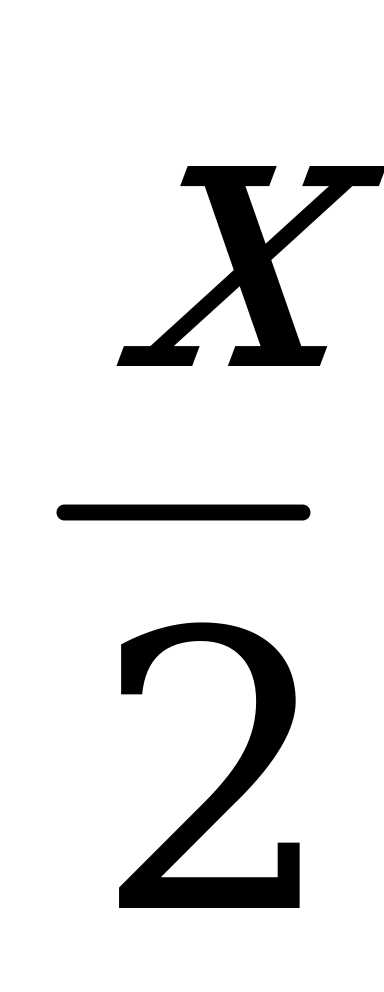 , получим
, получим
2sin2 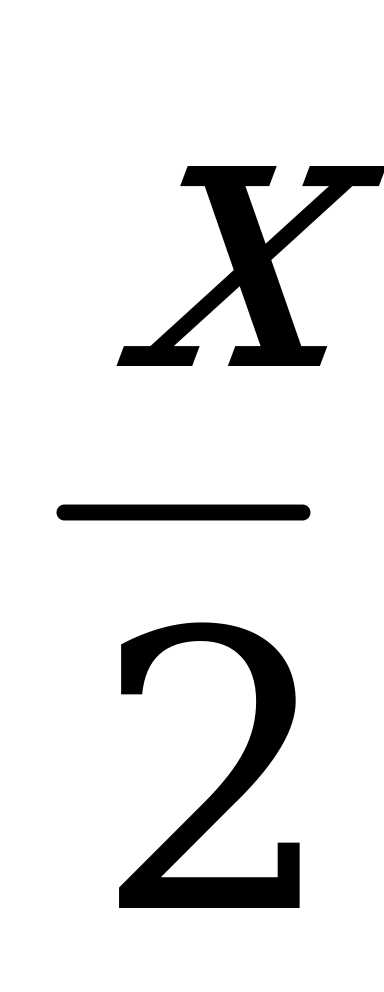 = 2sin
= 2sin 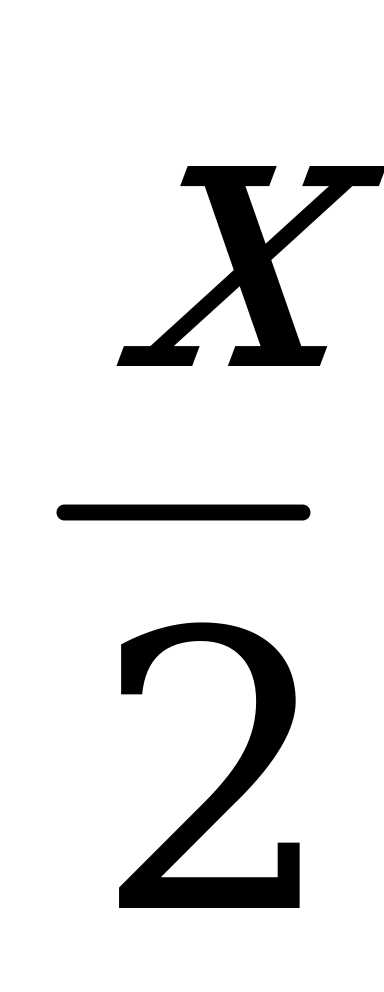 * сos
* сos 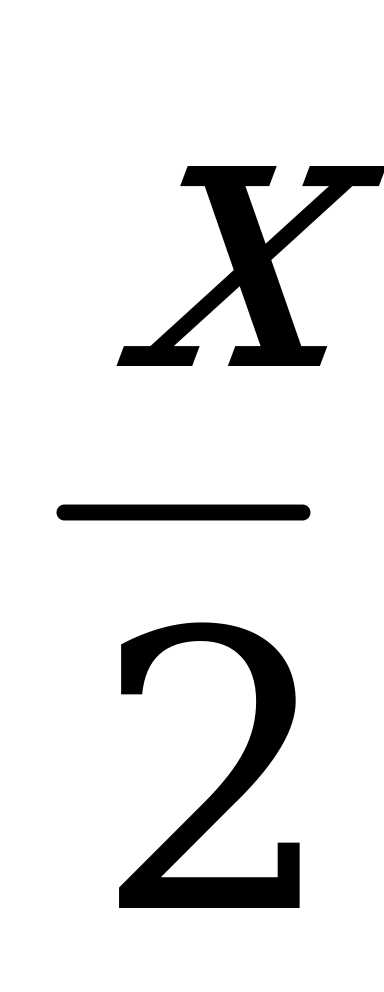 *sin
*sin 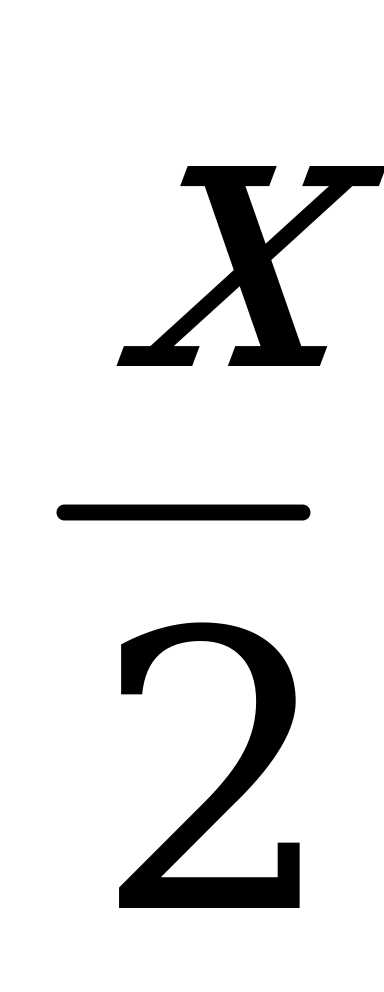 , разделим на 2 sin2
, разделим на 2 sin2 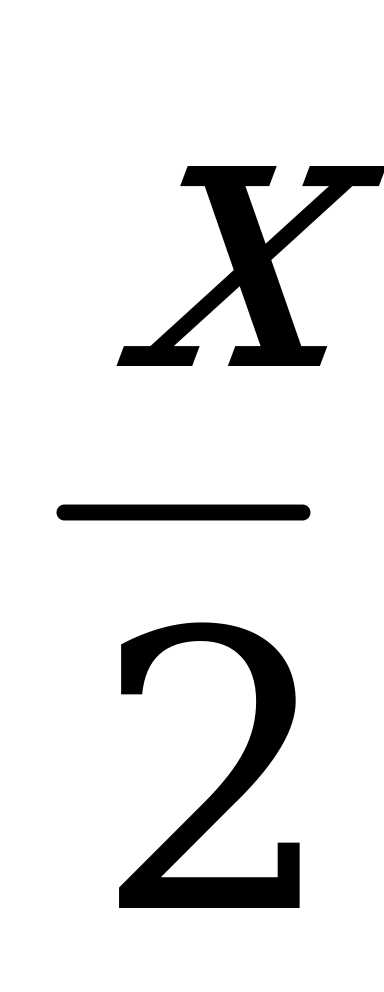 обе части уравнения, получим 1 = сos
обе части уравнения, получим 1 = сos 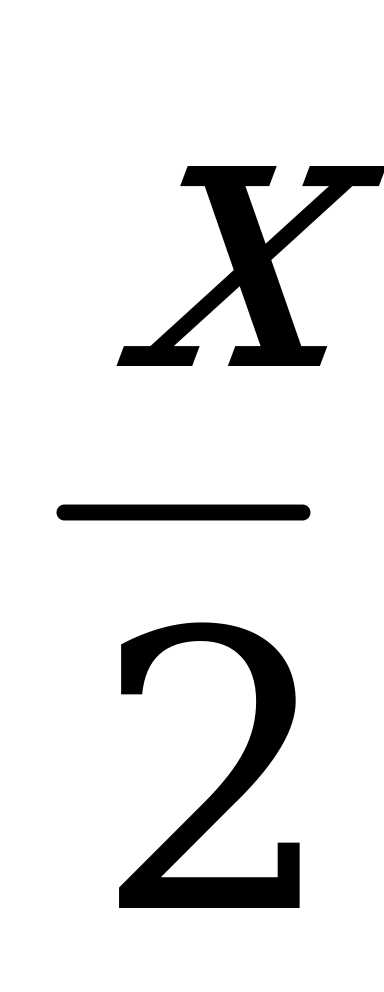 , решая это уравнение, найдем корни
, решая это уравнение, найдем корни 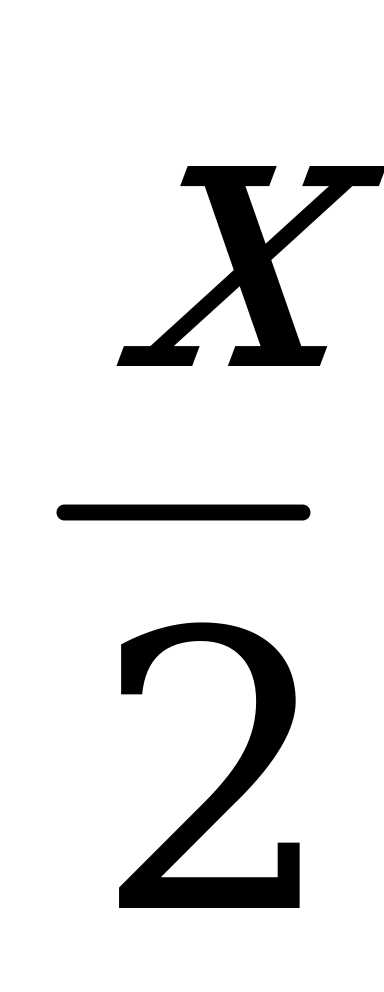 = 2 pn, x = 4pn, n
= 2 pn, x = 4pn, n 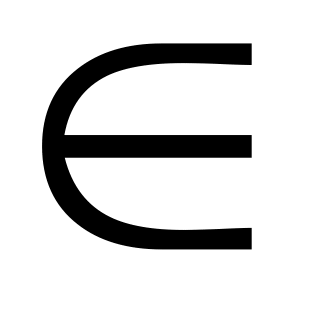 Z.
Z.
Потеряли корни sin 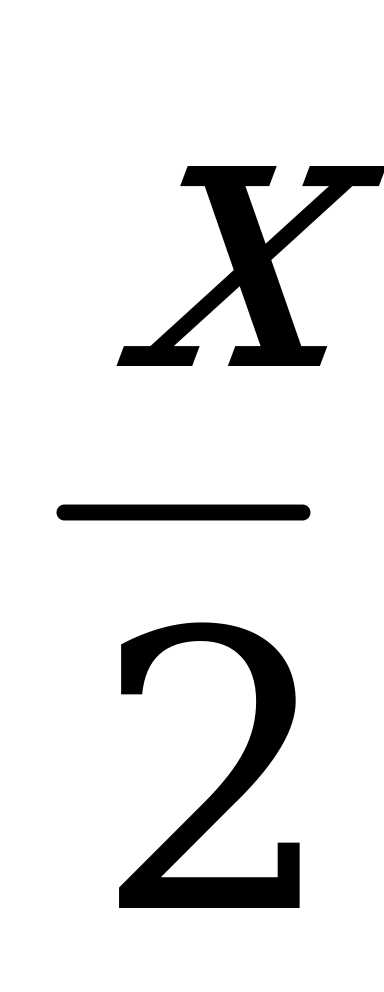 = 0, х = 2pk, k
= 0, х = 2pk, k 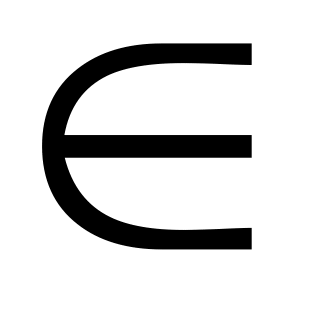 Z.
Z.
Правильное решение: 2sin2 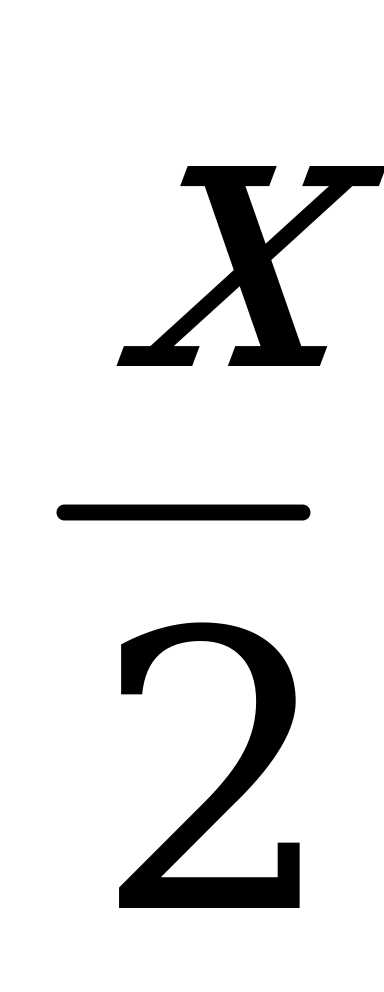 (1 – сos
(1 – сos 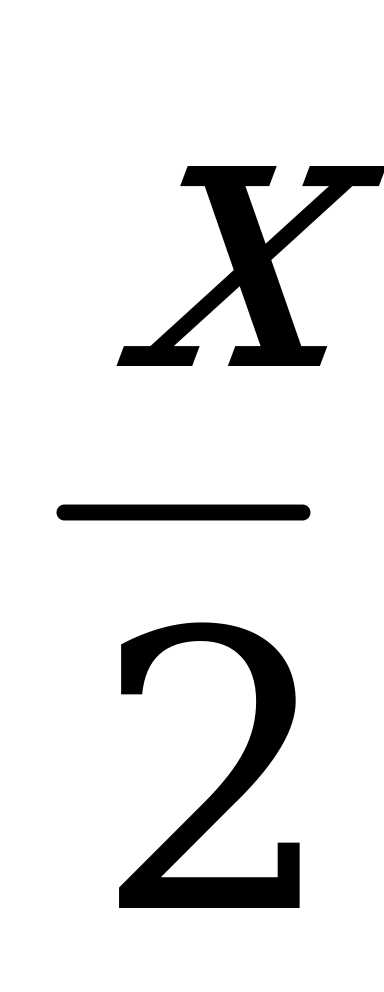 ) = 0.
) = 0.
sin2 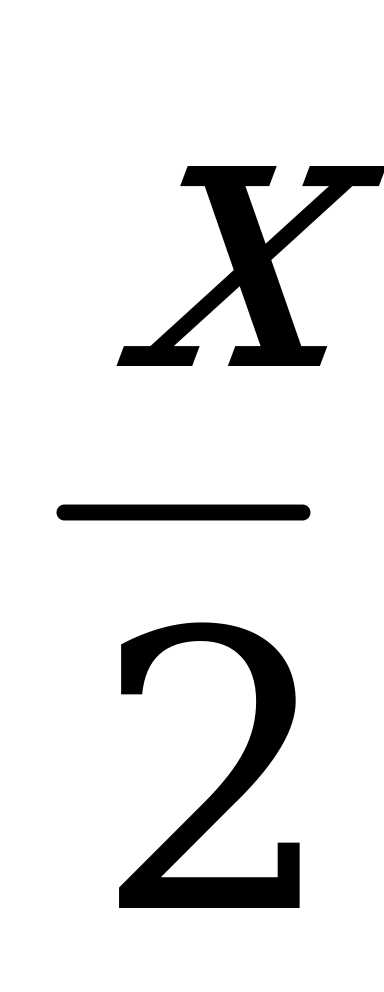 = 0 или 1 – сos
= 0 или 1 – сos 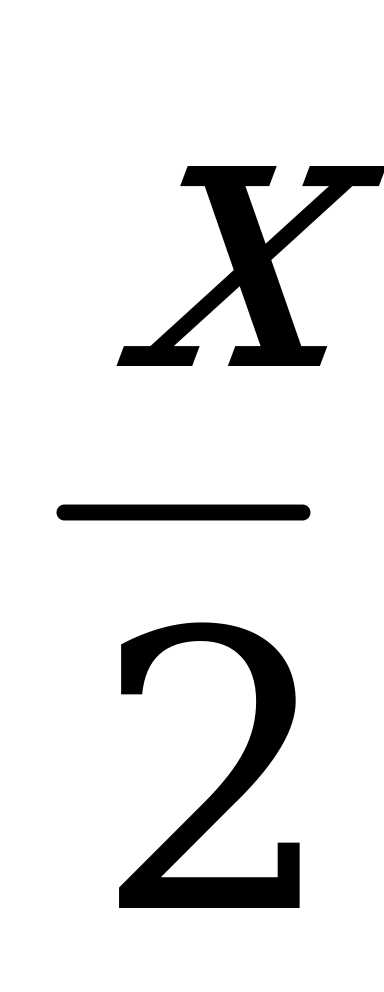 = 0
= 0
x = 2pk, k Z. x = 4pn, n Z.
Ответ: x = 2pk, k Z, x = 4pn, n Z.
2. Посторонние корни.
Решение.
О.Д.З.: sin 2x 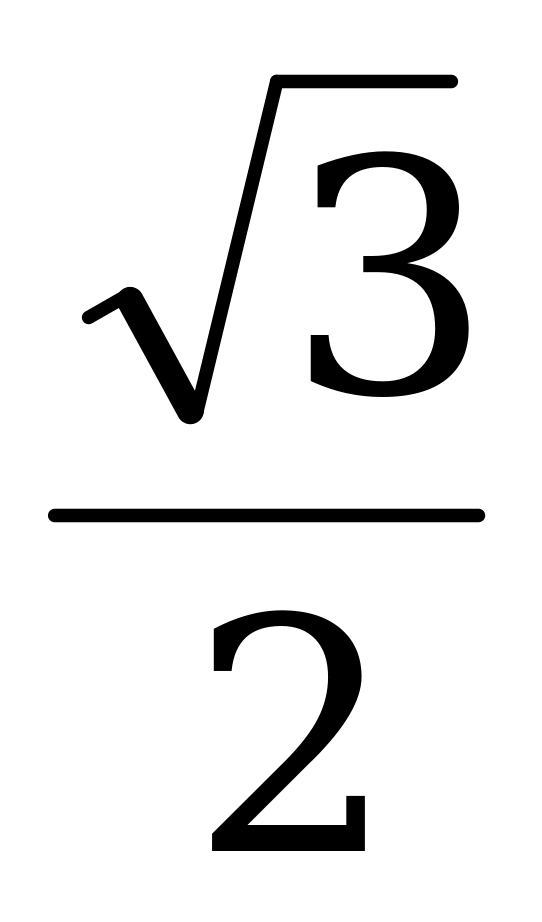 .
.
2сos 3х sinx – сos3x + 2sinx - 1 = 0
(сos3x + 1)(2sinx - 1) = 0
1. сos3x + 1 = 0, 2. 2sinx - 1 = 0
х =  +
+ 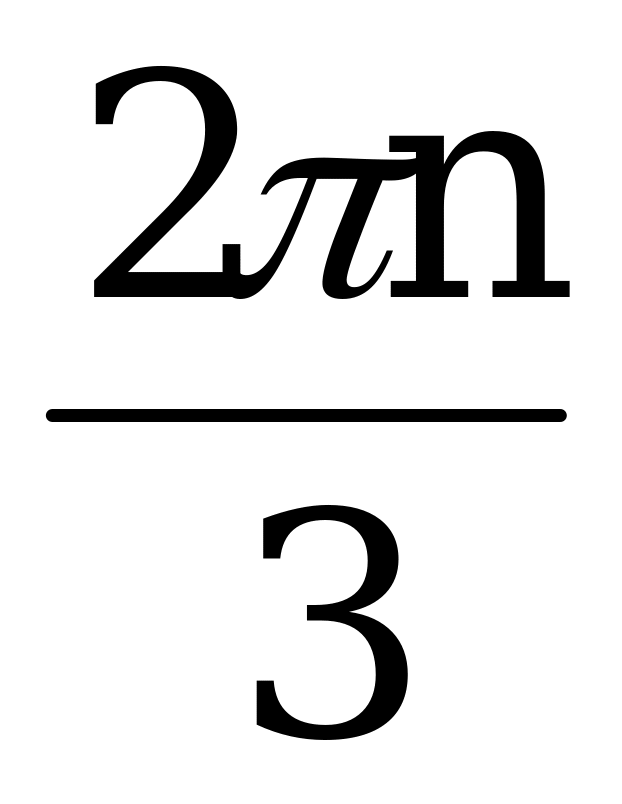 , n Z. x = (-1)k
, n Z. x = (-1)k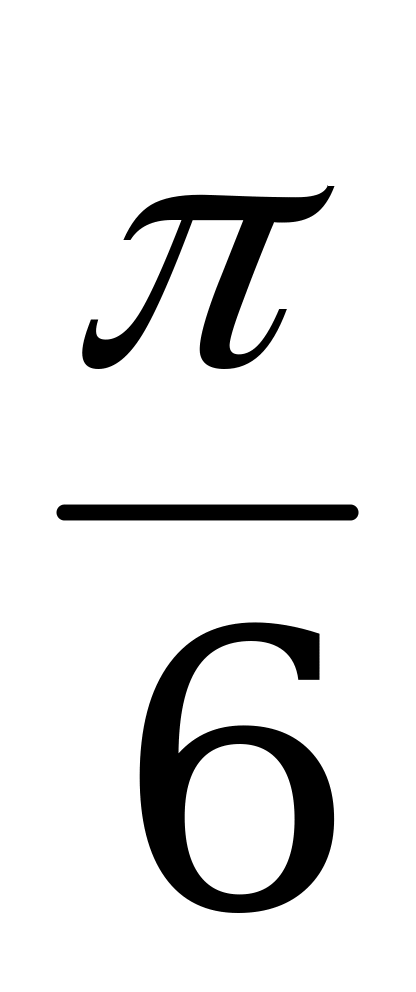 + pk, k Z.
+ pk, k Z.
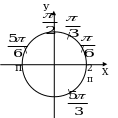 0 х
0 х
I. х = 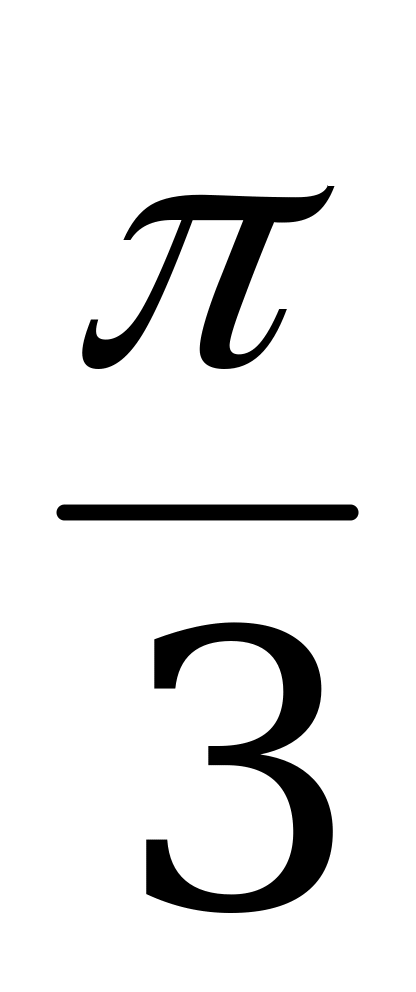 +
+ 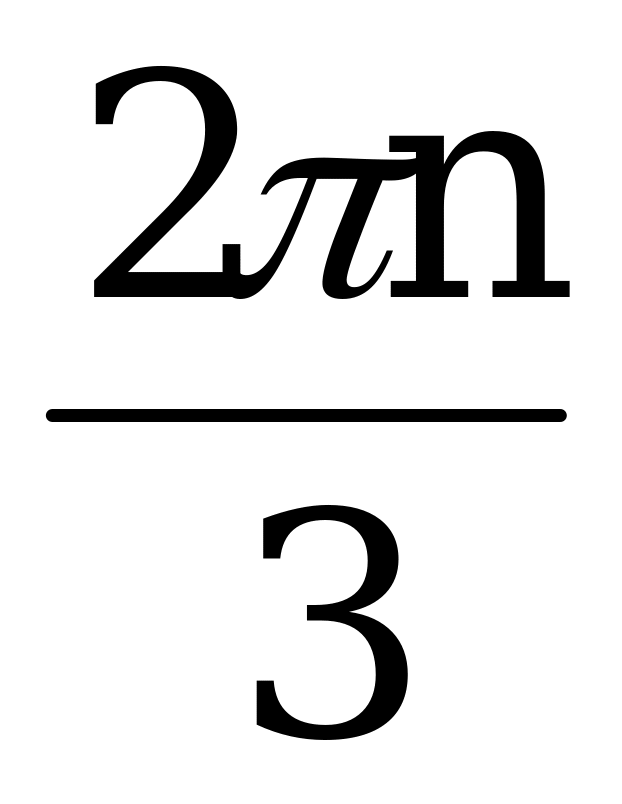 , n
, n 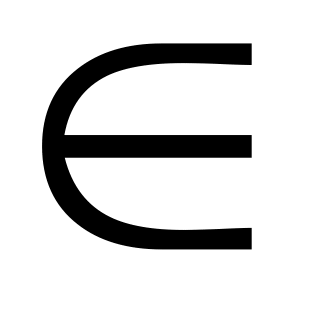 Z II. x = (-1)k
Z II. x = (-1)k 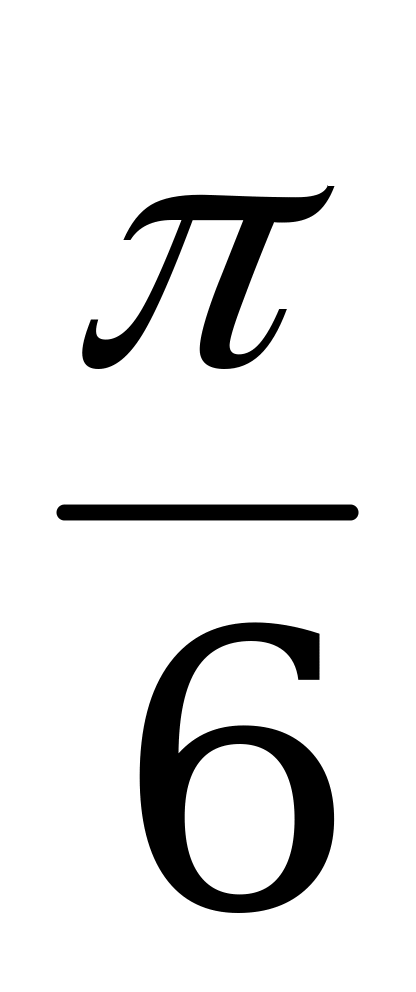 + pk, k
+ pk, k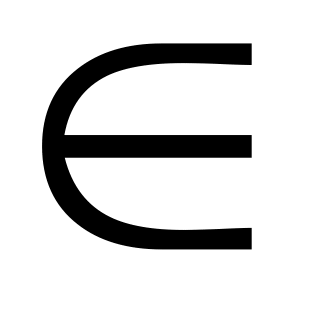 Z
Z
1. n = 0 1. k = 0
sin 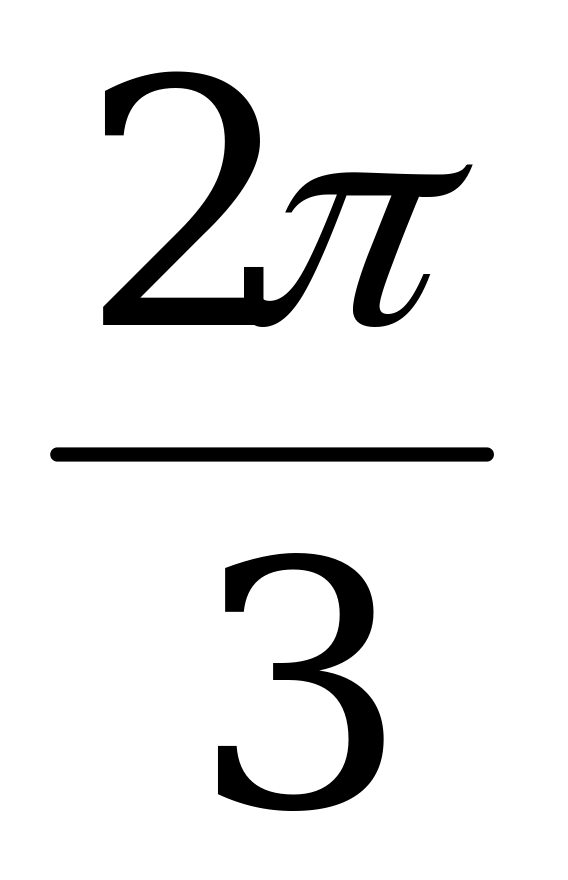 =
= 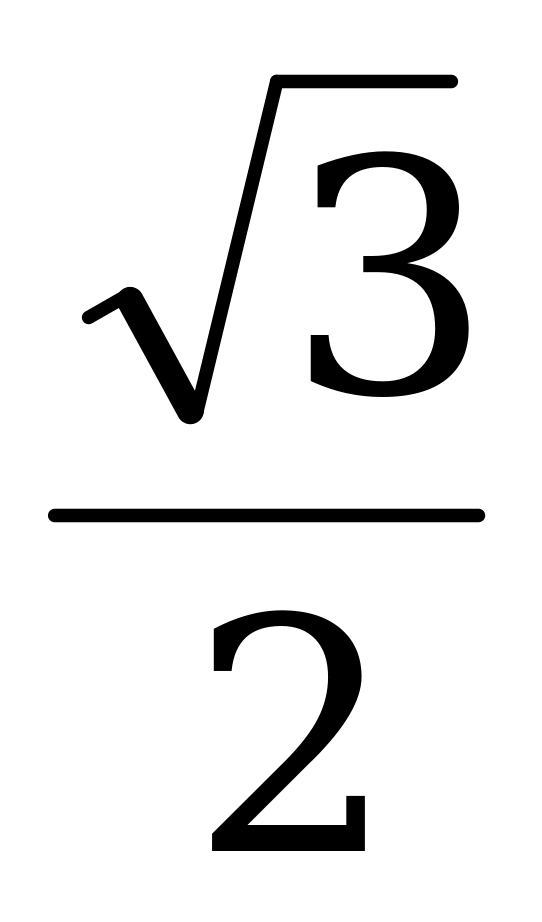 sin
sin 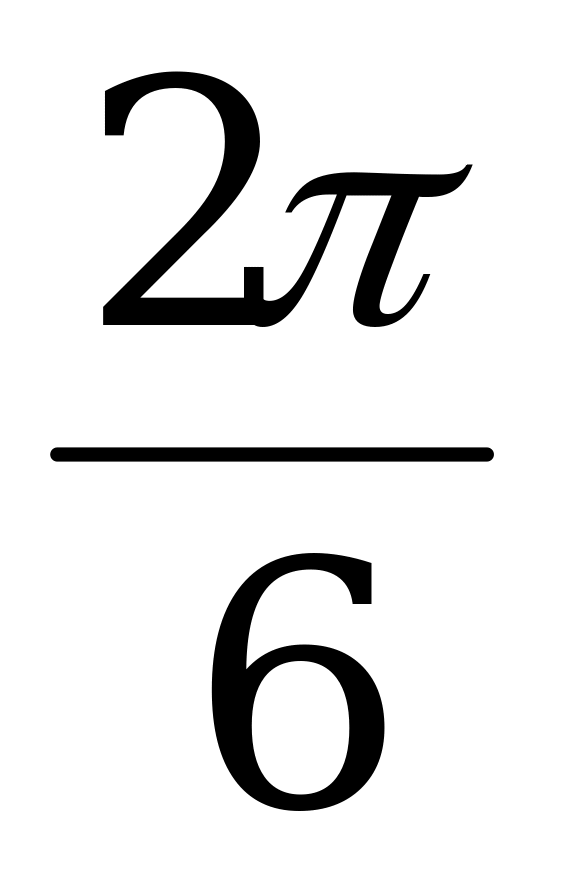 =
= 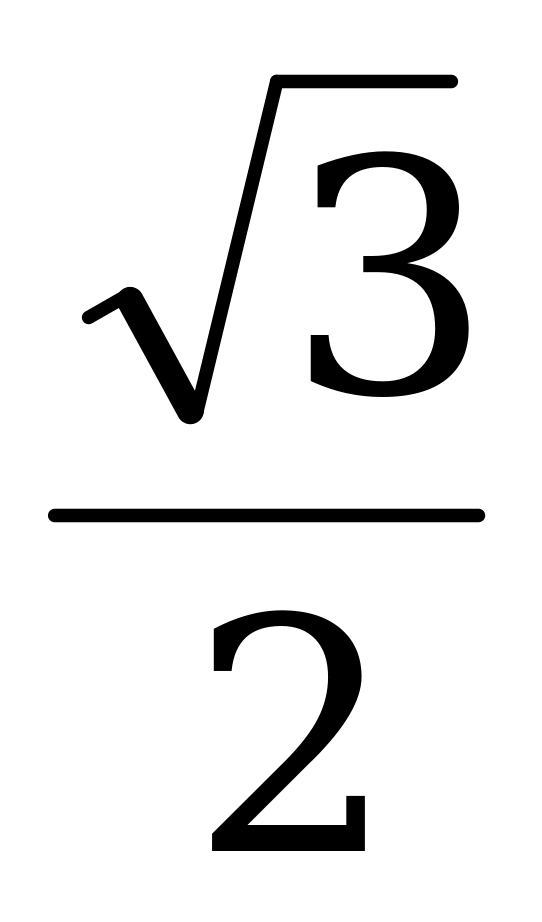
не удовл-т. О.Д.З. не удовл-т О.Д.З.
2. n = 1 2. k = 1
sin 2p = 0 sin 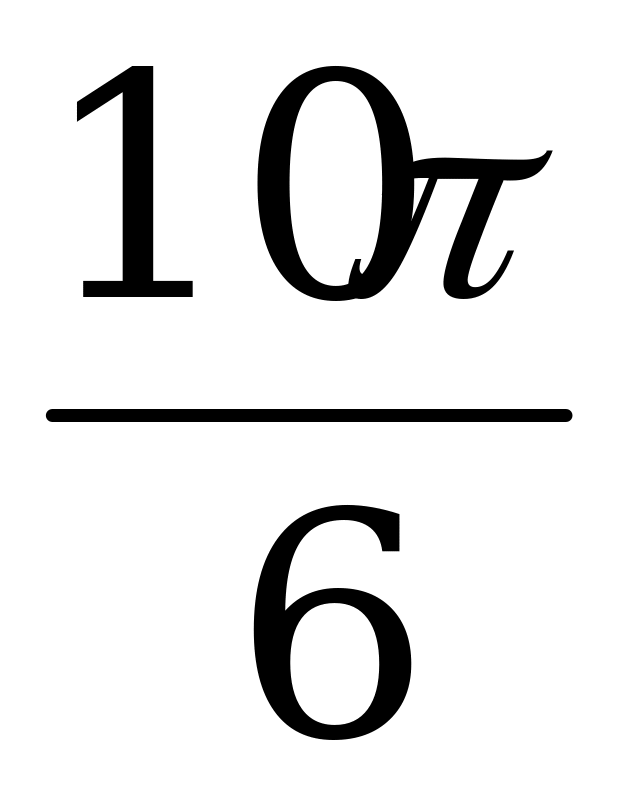 = -
= - 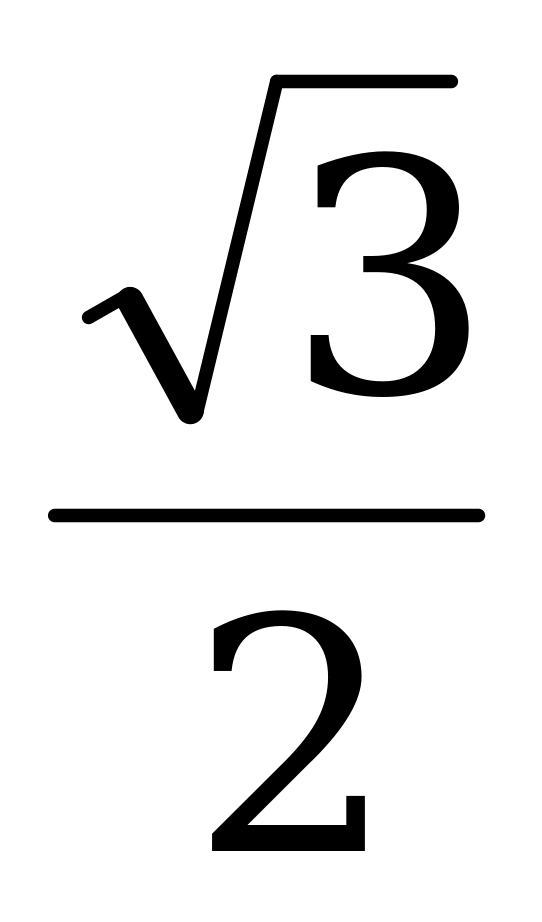
удовл-т О.Д.З. удовл-т О.Д.З.
3. n = 2
sin 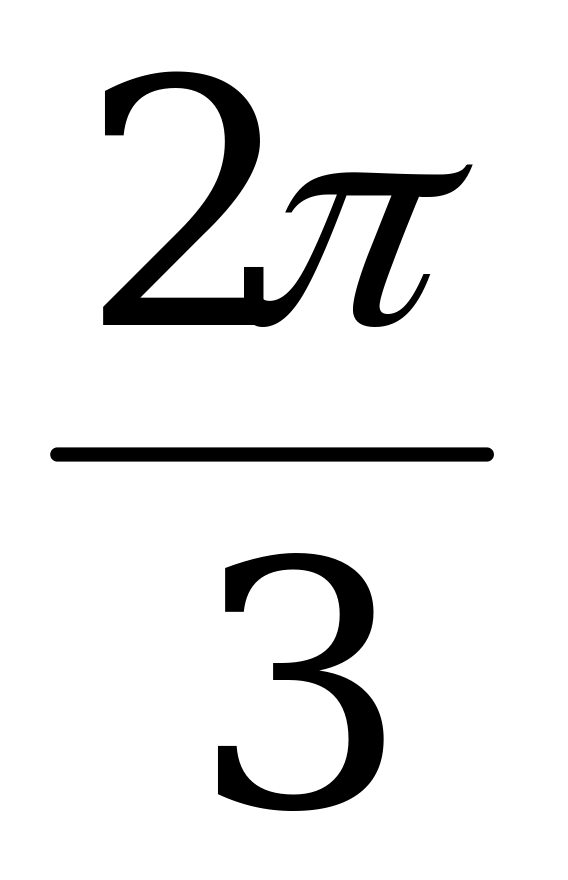 = -
= - 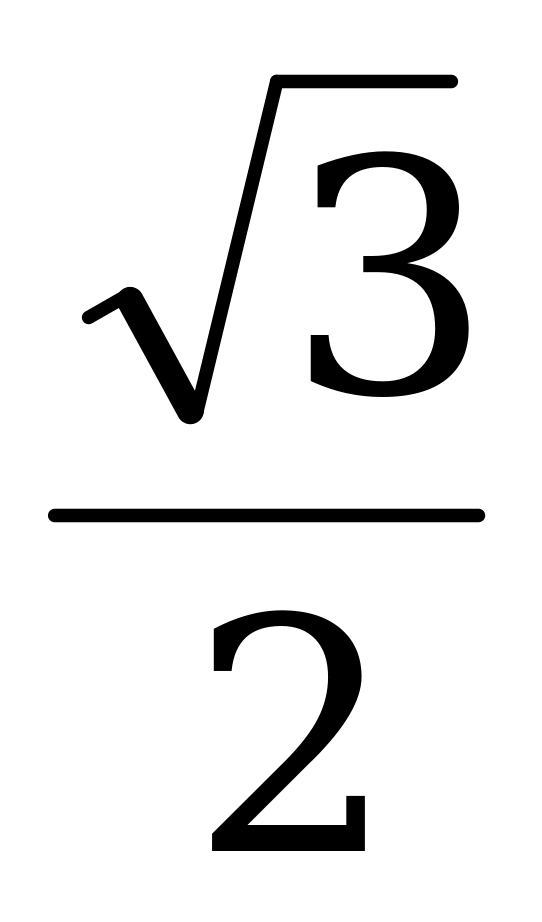
удовл-т О.Д.З.
Ответ: х = p + 2pk, x = 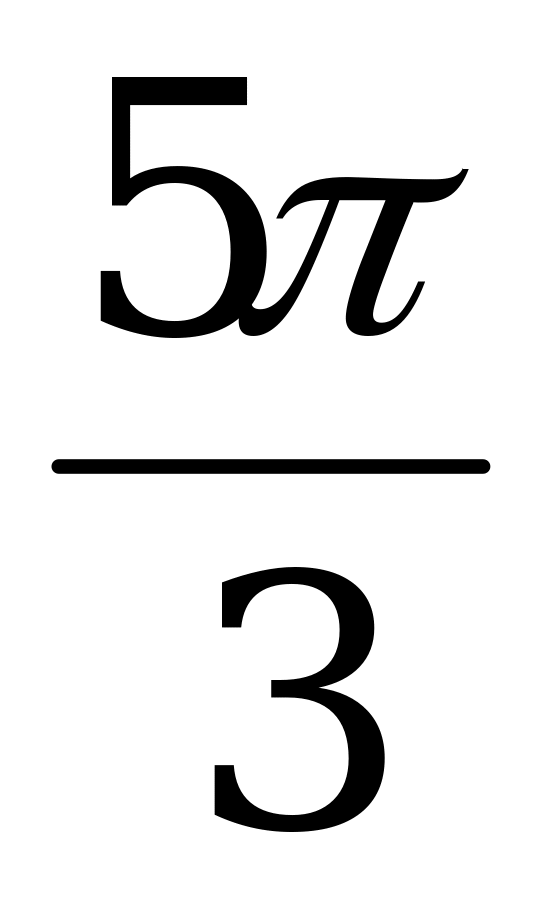 + 2pk, x =
+ 2pk, x = 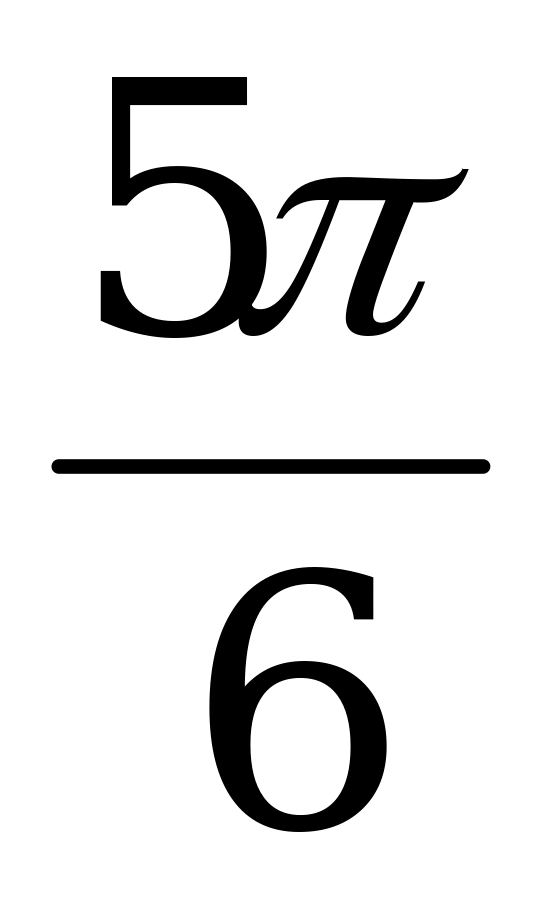 + 2pk, k Z.
+ 2pk, k Z.
Решение.
Введем подстановку t = 2x, получим 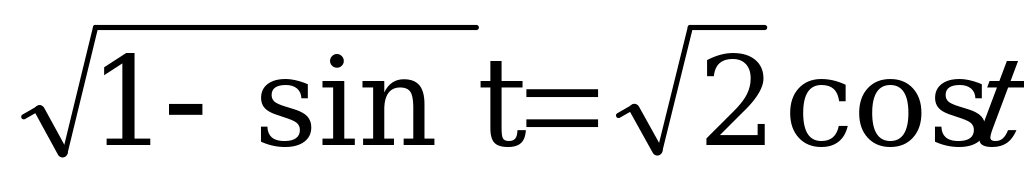 , где cos t 0,
, где cos t 0,
Возведем обе части уравнения в квадрат, получим 1 - sin t = 2 cos2 t, откуда
1. sin t = -1, 2. sin t = 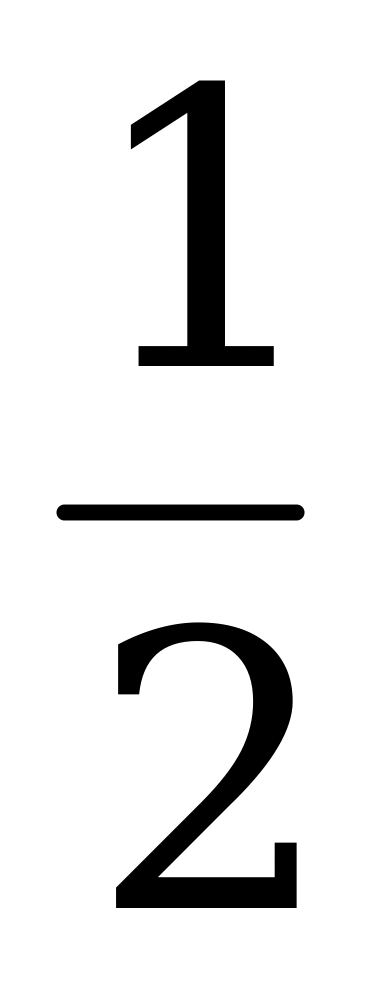 ,
,
t = -  + 2 pk, k Z; t = (-1)n
+ 2 pk, k Z; t = (-1)n 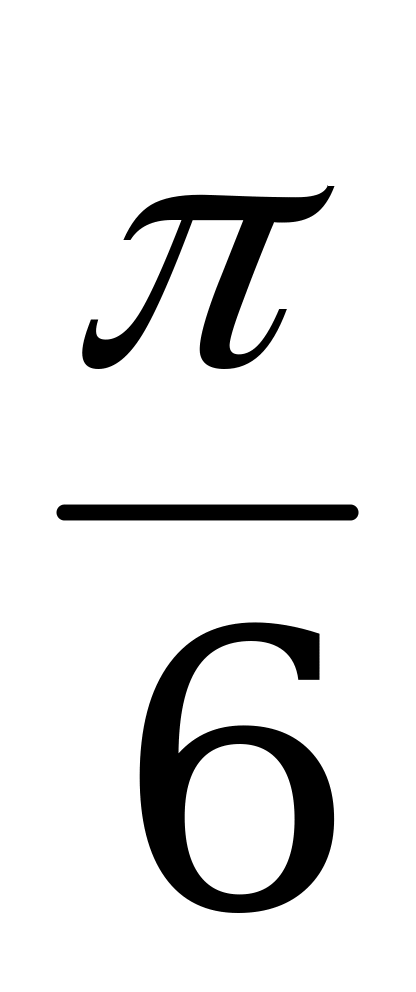 + pn, n Z;
+ pn, n Z;
-  t
t 
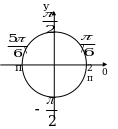 I. t = -
I. t = -  + 2 pk, k Z; II. t = (-1)n
+ 2 pk, k Z; II. t = (-1)n 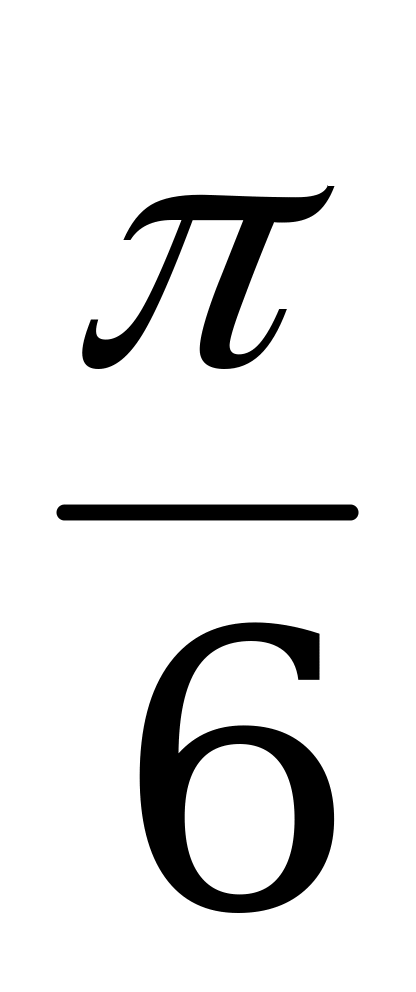 + pn, nZ;
+ pn, nZ;
1. k = 0, t = -  1. n = 0, t =
1. n = 0, t = 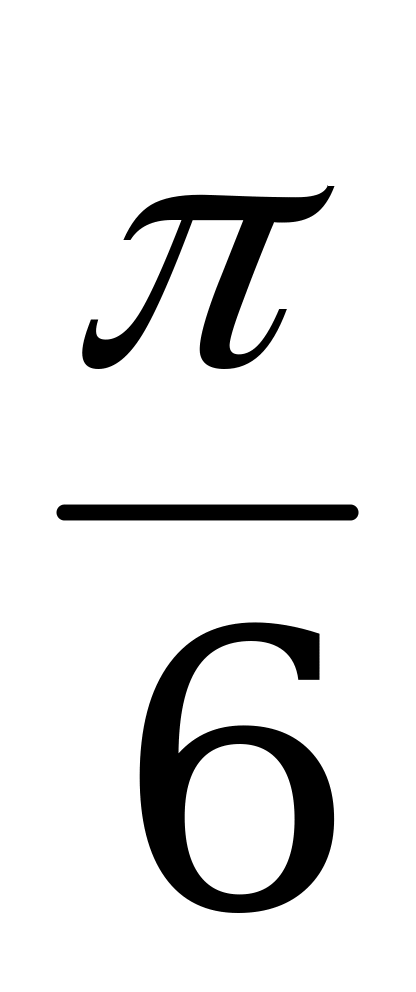
удовл-т ОДЗ. удовл-т О.Д.З.
2. n = 1, t = 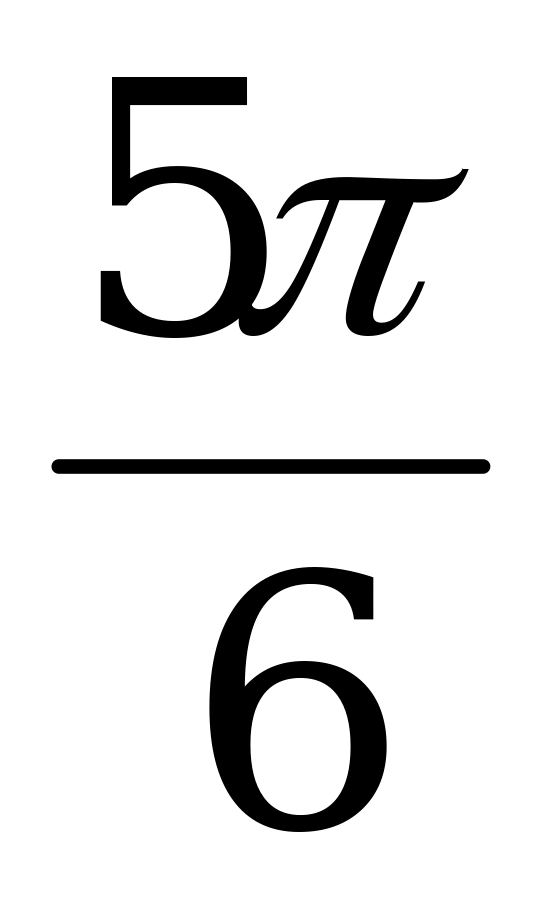
не удовл-т О.Д.З.
Ответ: t = -  + 2 pk, t =
+ 2 pk, t = 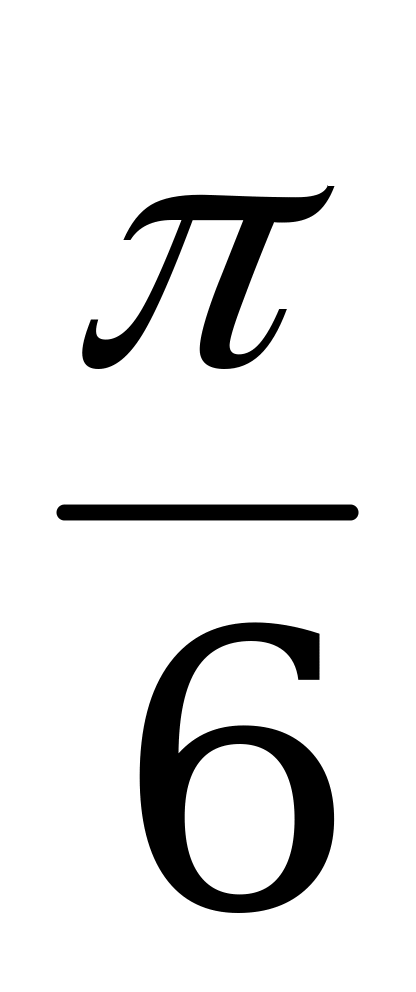 + 2 pn,
+ 2 pn,
x = - 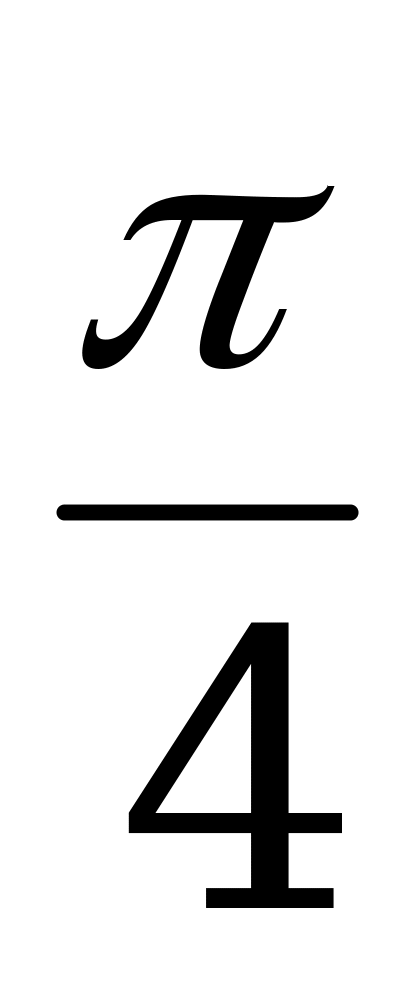 + pk, k
+ pk, k 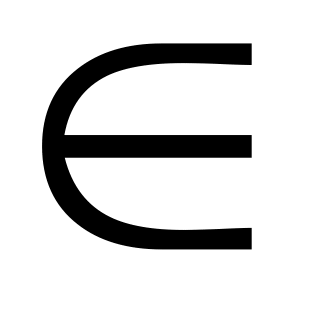 Z, x =
Z, x = 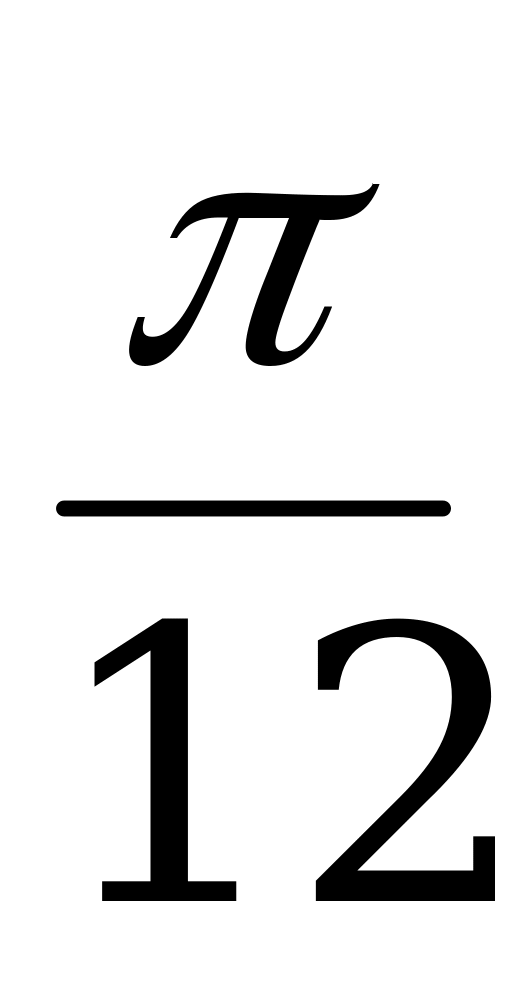 + pn, n
+ pn, n 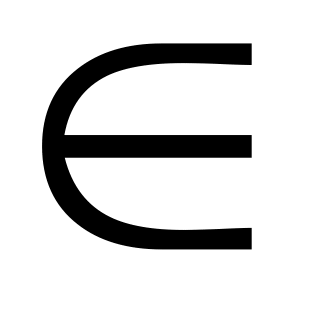 Z.
Z.
3. Отбор корней.
Решение.
О.Д.З.: х  + pk, x
+ pk, x 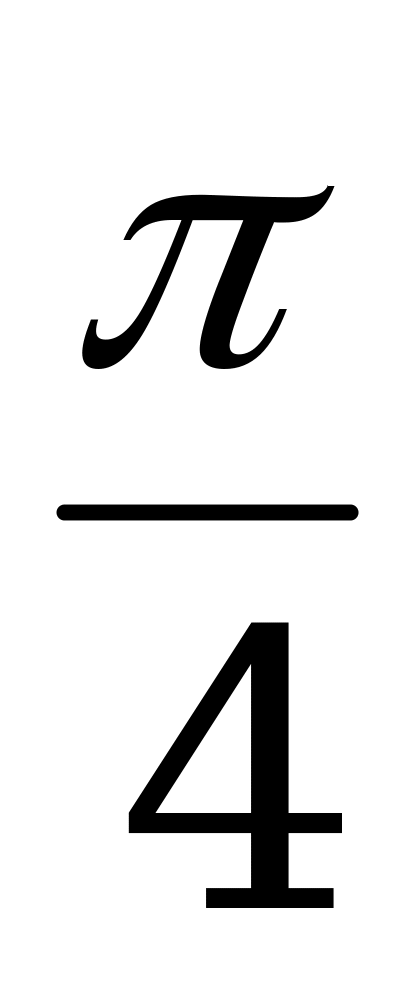 + pk, x
+ pk, x 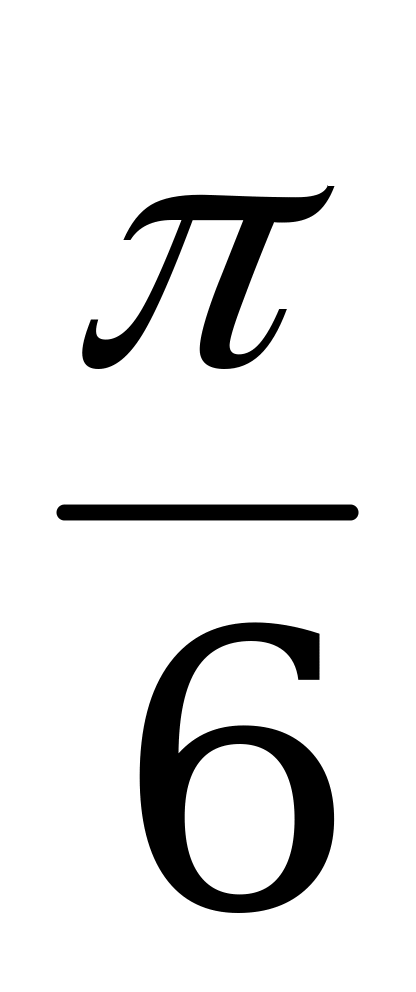 + pk, k Z.
+ pk, k Z.
Заменим tgx + tg2x = 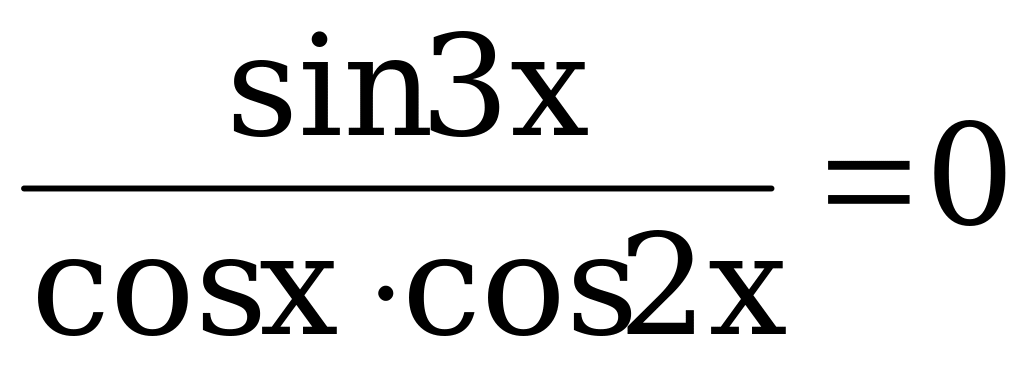 , а tg3x =
, а tg3x = 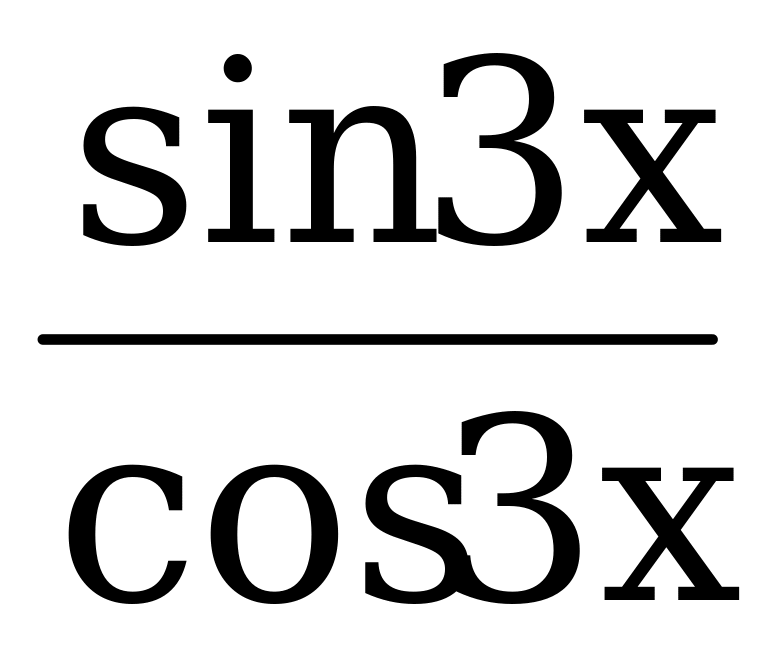 , получим
, получим
sin3x (cos3x - cosx cos2x) = 0, sin3x ((cos2x cosx – sin2x sinx) – cosx cos2x) = 0,
sin3x*sinx*sin2x = 0.
1. sin3x = 0 2. sinx = 0 3. sin2x = 0
x = 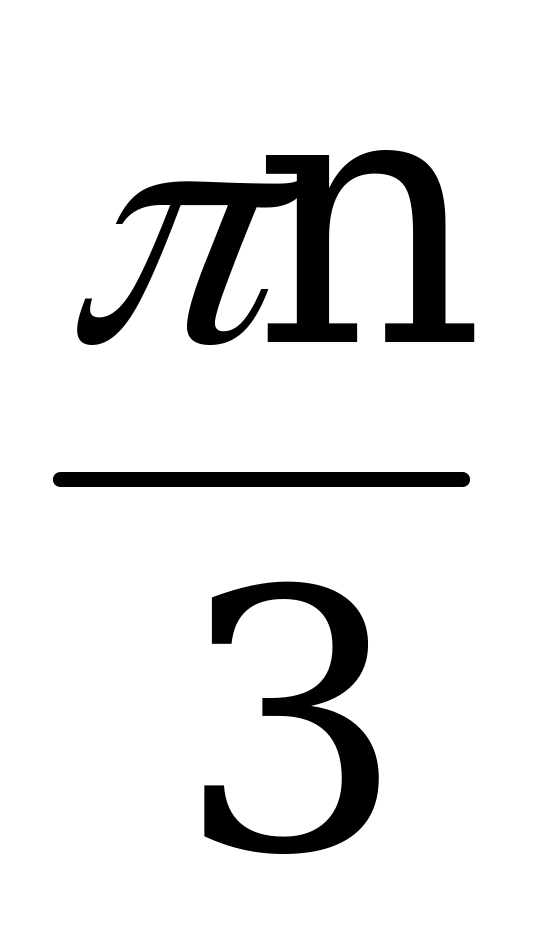 , n Z, x = ph, h Z, x =
, n Z, x = ph, h Z, x = 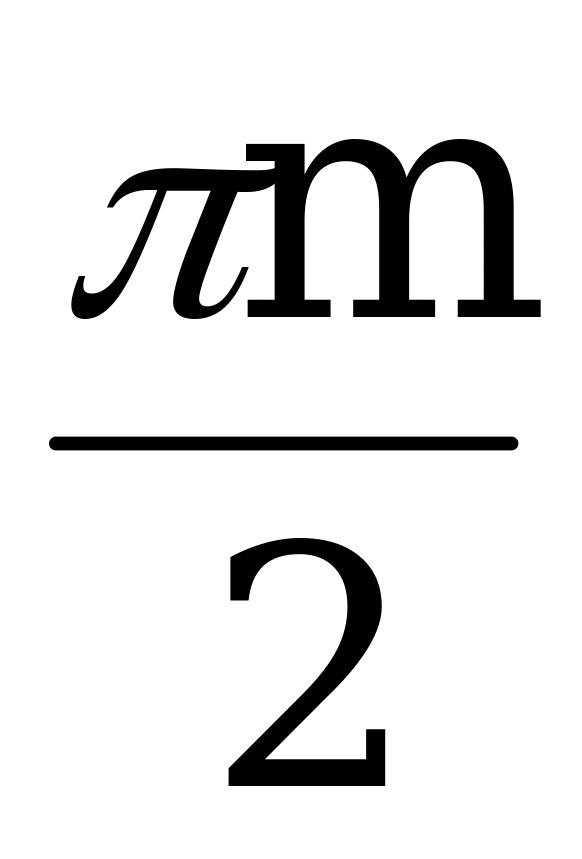 , m Z.
, m Z.
n = 0, x = 0 уд. h = 0, x = 0 уд. m = 0, x = 0 уд.
n = 1, x = 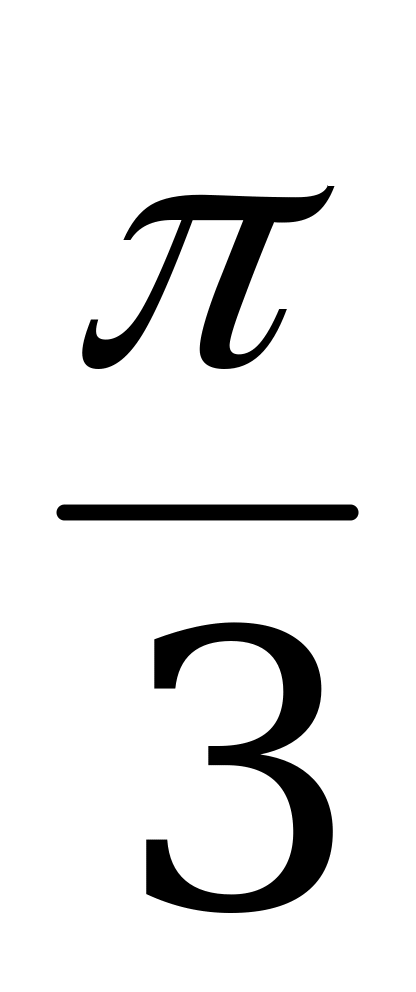 уд. h =1, x = p уд. m = 1, x =
уд. h =1, x = p уд. m = 1, x =  не уд.
не уд.
n = 2, x = 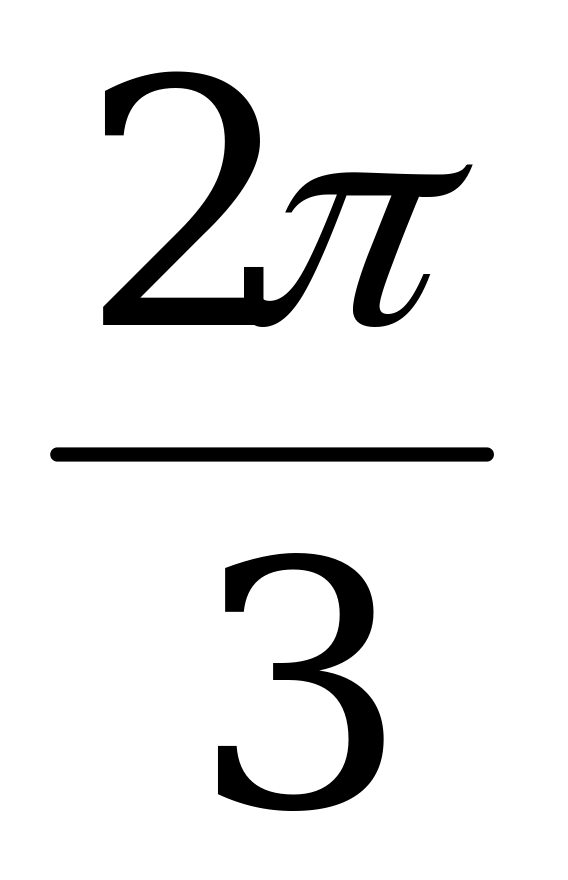 уд. h = 2, x = 2 p уд. m = 2, x = уд.
уд. h = 2, x = 2 p уд. m = 2, x = уд.
n = 3, x = p уд. m = 3, x = 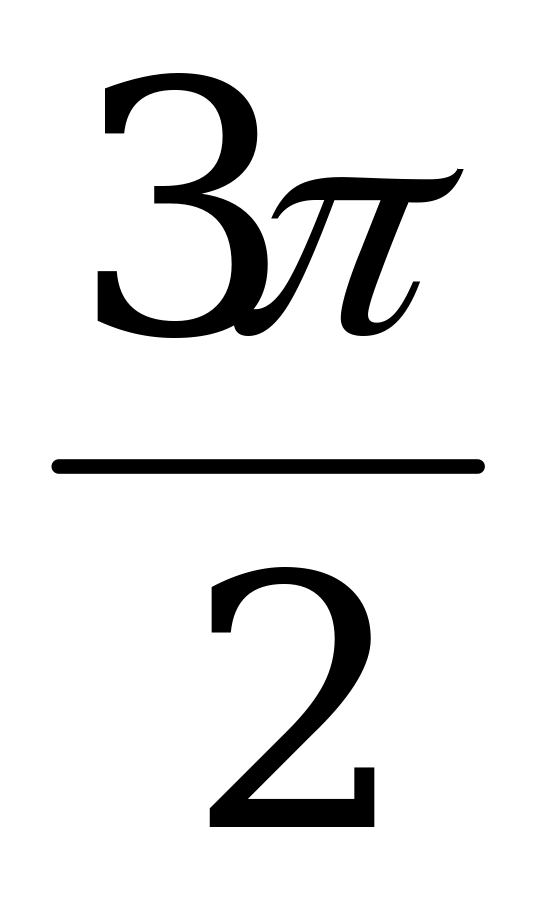 не уд.
не уд.
n = 4, x =
= 4, x = 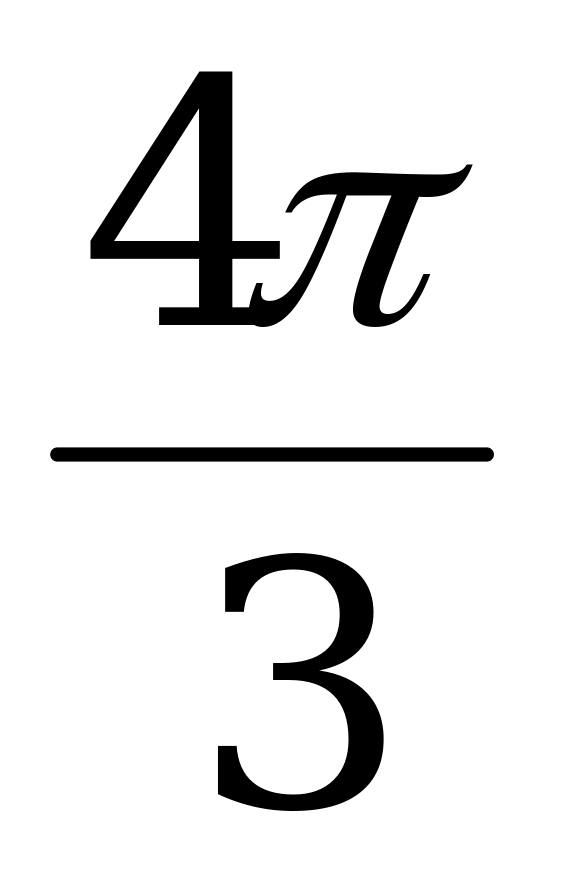 уд.
уд.
n = 5, x = 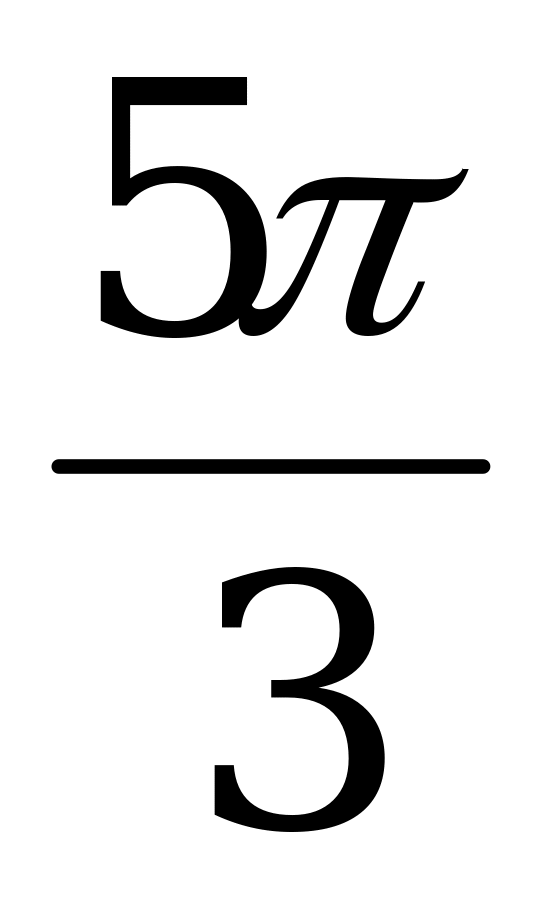 уд.
уд.
Ответ: x = 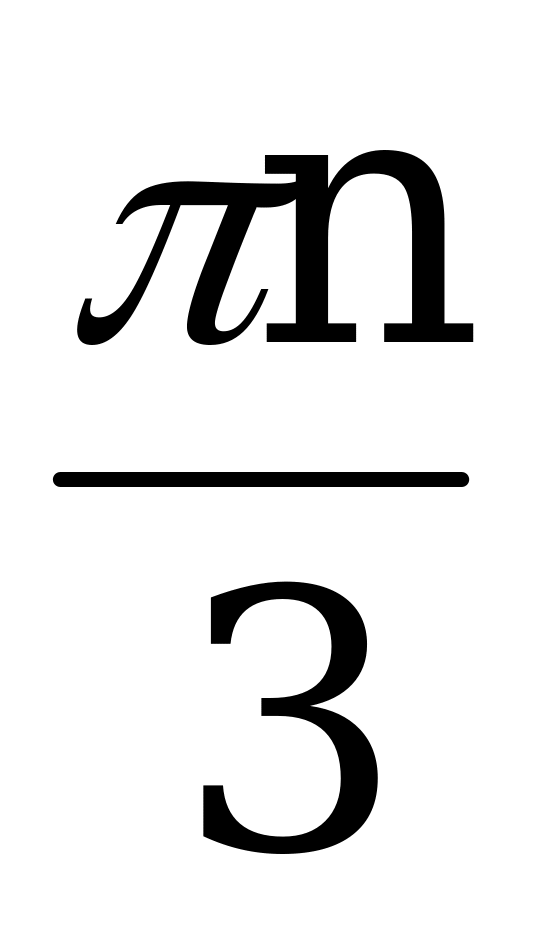 , n Z.
, n Z.
IV. Подведение итогов семинара.
9







 ст. A sinx + B cosx = 0 : cosx A tg x + B = 0 II ст. A sin2 x + B sinx cosx + A cos2 x = 0 : cos2x A tg2 x + B tgx + C = 0
ст. A sinx + B cosx = 0 : cosx A tg x + B = 0 II ст. A sin2 x + B sinx cosx + A cos2 x = 0 : cos2x A tg2 x + B tgx + C = 0 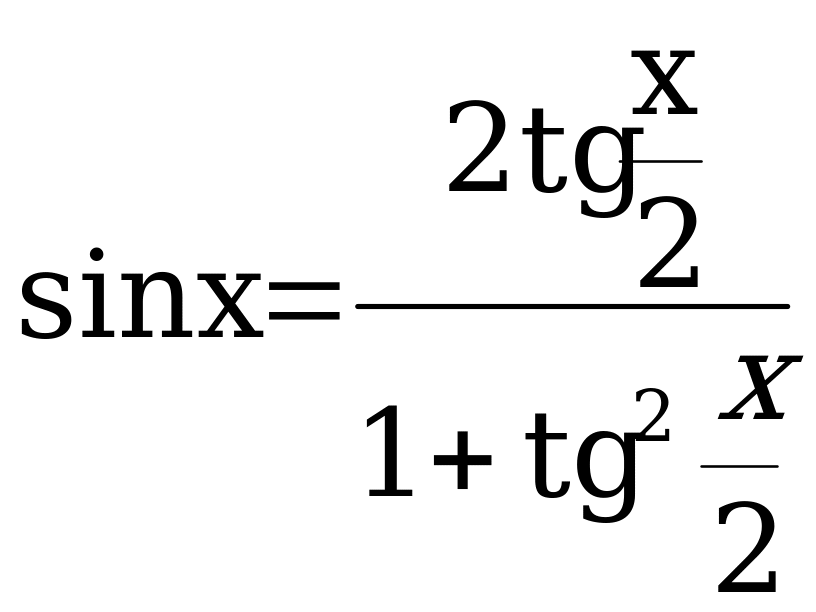 ;
; 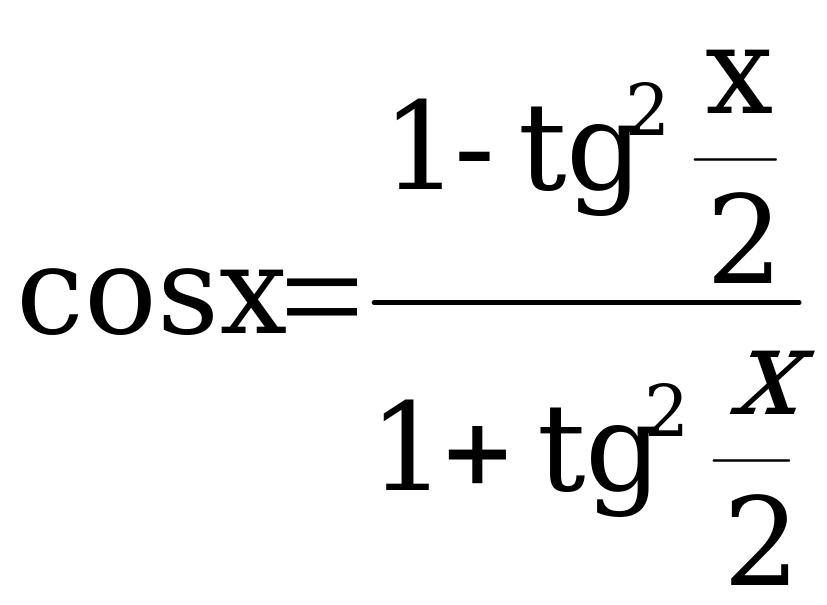 ;
; 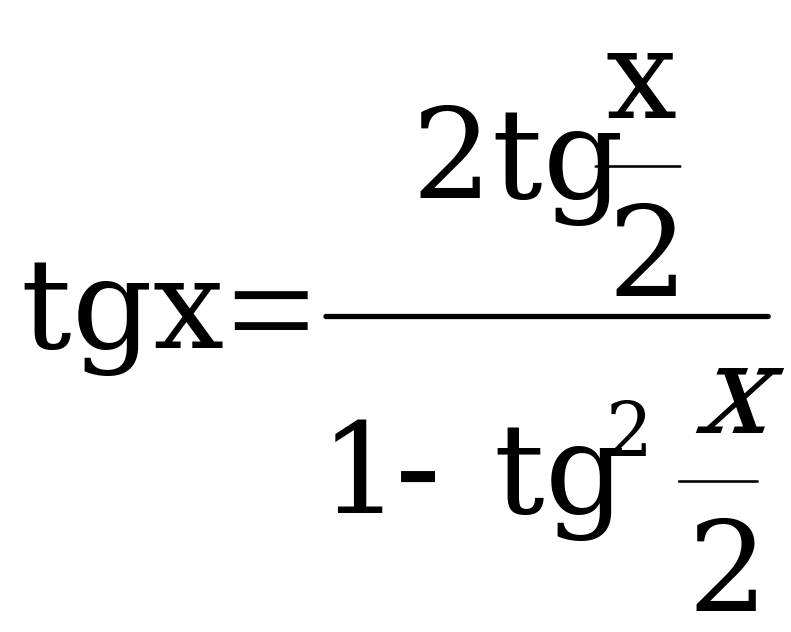 . х + 2n; Проверка обязательна!
. х + 2n; Проверка обязательна!  оспользуемся функционально-графическим методом.
оспользуемся функционально-графическим методом. 0 х
0 х  I. t = -
I. t = -  = 4, x =
= 4, x = 









