Просмотр содержимого документа
«Квадратный разности»

« Дорогу осилит
идущий,
а математику
– мыслящий!»

Теория «Действия с Многочленами»
Сложение и
вычитание
многочленов
Умножение
многочлена
на многочлен
Умножение
многочлена
на одночлен
Многочлен
Запись многочлена
в стандартном
виде

Повторение «Возведение одночлена в степень»
100
Найдите квадраты
выражений
Представьте
в виде
квадрата

Повторение : «Найти удвоенное
произведение одночленов»
0,4х и
3b и - 5с
а и b
0, 5у и 6
Перемножьте многочлены
(х+2) ·(у -2)
( 3 – c) · (4 + b)

№ парты
1
I задание
(y+b)(y+b)
2
II Запишите в виде степени
(c +d)(c + d)
III ответ
3
(x +2)(x +2)
4
(x – y)(x - y)
5
6
(m – n)(m-n)
(a – 2)(a - 2)

Взаимопроверка
№
1
I
2
задание
II
(y+b)(y+b)
Запишите в виде степени
3
(c +d)(c + d)
III
4
(x +2)(x +2)
ответ
5
(x – y)(x - y)
(m – n)(m-n)
6
(a – 2)(a - 2)

Взаимопроверка
№
1
I
2
(y+b)(y+b)
задание
II
3
III
(c +d)(c + d)
Запишите в виде степени
(x +2)(x +2)
ответ
4
5
(x – y)(x - y)
(m – n)(m-n)
6
(a – 2)(a - 2)

Взаимопроверка
№
1
I
2
задание
II
(y+b)(y+b)
Запишите в виде степени
3
(c +d)(c + d)
III
4
(x +2)(x +2)
ответ
5
(x – y)(x - y)
(m – n)(m-n)
6
(a – 2)(a - 2)

«Дорогу осилит идущий,
а математику –мыслящий!»
Тема Урока «ВОЗВЕДЕНИЕ В КВАДРАТ СУММЫ И РАЗНОСТИ ДВУХ ВЫРАЖЕНИЙ»

Тема урока:
Возведение в квадрат суммы и разности двух выражений.
Цель урока: Познакомиться с формулами квадрат суммы и квадрат разности двух выражений
Задача урока: научиться алгоритму работы с формулами.
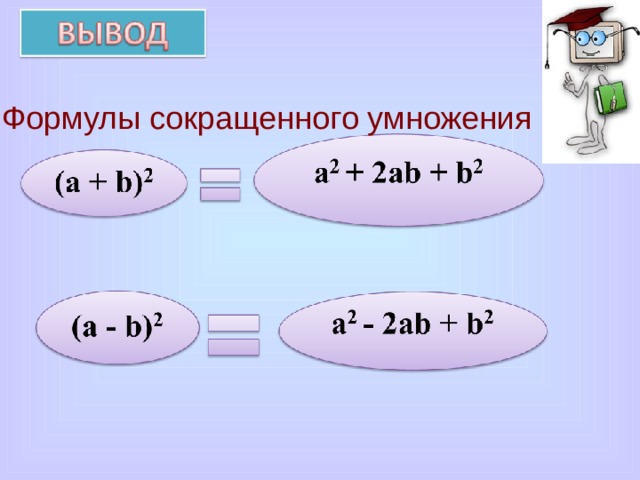
Формулы сокращенного умножения
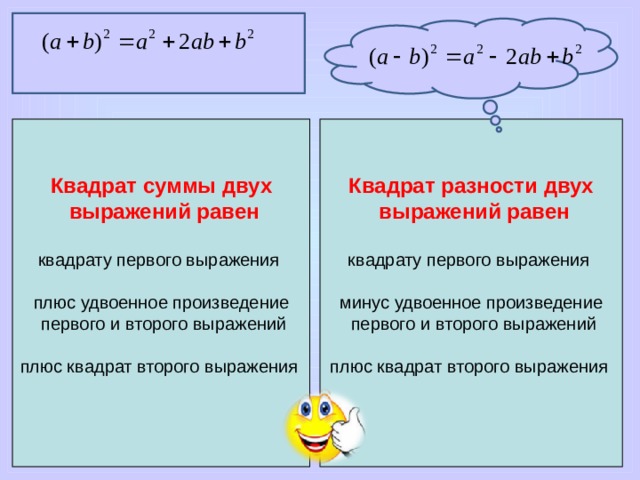
Квадрат разности двух
Квадрат суммы двух
выражений равен
выражений равен
квадрату первого выражения
квадрату первого выражения
минус удвоенное произведение
плюс удвоенное произведение
первого и второго выражений
первого и второго выражений
плюс квадрат второго выражения
плюс квадрат второго выражения

АЛГОРИТМ применения формул:
- 1. найти квадрат первого числа
- 2. найти удвоенное произведение первого и второго числа
- 3. найти квадрат второго числа
- (смотри знаки. Перед квадратом второго числа всегда плюс +; перед удвоенным произведением знак по знаку в скобках)
- ( х – 2с) = х - 2·х ·2с + (2с) = х – 4хс + 4с

Заполнить таблицу
№
Выражение
1
Квадрат 1
(а + 4) 2
2
Удвоенное произведение
3
выражения
(8 - х) 2
(2y + 1) 2
Квадрат 2
Результат
выражения

Возведи в квадрат

Применение полученных знаний.
Вычисли: 1)
= 3600 – 120 + 1 = 3480 + 1 =3481

Дешифратор «Имя великого ученого»
И -5) (с + 6)
Задание
Задание
Л - 4) (х – 3)
Д 6) (3 – 5b)

Найди букву:
- Е- 49 -14а + Л -х - 6х + 9
- В- + 10а + 25 И - с +12с + 36
- К- 9у - 12у + 4 Д- 9 + 30b + 25b
ЕВКЛИД

Евклид (ΙΙΙ в. до н. э.)
Древнегреческий математик, автор знаменитого трактата «Начала», посвященного элементарной геометрии, теории чисел. Оказал огромное влияние на развитие математики .

Евклид. «Начала». Издание 1482 г.
Вот что писал Евклид в своей книге «Начала»: «Если отрезок как-либо разбит на два отрезка, то площадь квадрата, построенного на всем отрезке, равна сумме площадей квадратов, построенных на каждом из двух отрезков, и удвоенной площади прямоугольника, сторонами которого служат эти два отрезка».

a
b
b
a
Геометрический смысл формулы (a+b) 2 =а 2 +2ab+b 2 учебное пособие стр 164 рис. 70

a
b
a
b
Геометрический смысл формулы (a-b) 2 =а 2 -2ab+b 2 учебное пособие №801


Домашнее задание
1 . творческое задание
(см.рисунок)
2. Учебник
стр. п32 (правила)
3. Формулы

Итог урока
- -С какими формулами мы познакомились сегодня на уроке?
- -Почему эти формулы называются формулами сокращенного умножения?
- -Чему равен квадрат суммы двух выражений?
- -Чему равен квадрат разности двух выражений?
- -Как вы думаете, зачем нужны нам эти формулы и стоит ли их запоминать?
На уроке мы:
П овторяли
О шибались,
Л атали прорехи в своих знаниях
И сследовали
Н аходили верное решение
О бучали друг друга
М ыслили!

Цели :
1. Получить новые знания
Учебные элементы
2. Показать свои знания
Кол-во баллов
3. Получить хорошую оценку
1. Математическая речь
2. Задание с выбором ответа
4.
3. Ты – мне, я – тебе
5.
4. Дешифратор
5. Работа в паре «Геометрическая интерпретация формулы»

Спасибо











































