Решение одной задачи несколькими способами. 11 класс.
Задача.*
Основанием прямоугольного параллелепипеда является квадрат площадью 10  Боковое ребро
Боковое ребро  см. Найти расстояние между стороной основания и диагональю, не имеющей с ней общих точек.
см. Найти расстояние между стороной основания и диагональю, не имеющей с ней общих точек.
Применим различные методы исследования к данной задаче.
Метод проекций.
Метод объёмов.
По определению
Метод координат.
Метод проекций
Выбираем плоскость (ВВ1С1С), перпендикулярную одной из скрещивающихся прямых АВ.
Проецируем каждую прямую на эту плоскость. Проекция АВ – это точка В. Проекция  - В1С.
- В1С.
Расстояние между проекциями будет расстоянием между скрещивающимися прямыми – это ВК.
Расстояние между скрещивающимися прямыми можно определить как расстояние между ортогональными проекциями этих прямых на плоскость проекций.
Решение.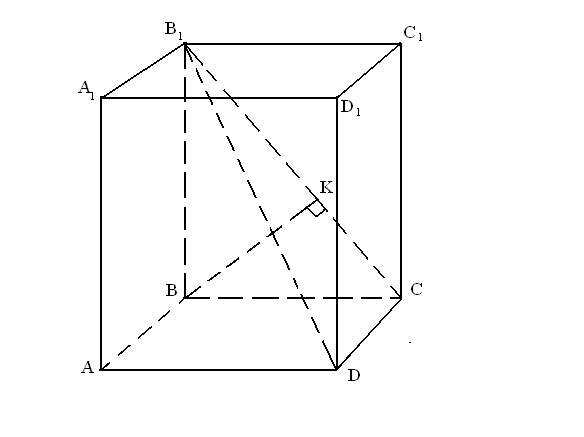
ВС = 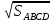 =
=  cм
cм
Рассмотрим ∆ АВ1В (∟В1ВС = 900)
Теорема Пифагора
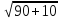 =10= В1С
=10= В1С
4. S=½BK* В1С
5. S=½*3 *
* =15
=15
6. 30=BK*10
7. BK=3
Метод объемов
Решение.
1.Рассмотрим пирамиду 

2. По теореме Пифагора 
3. Рассмотрим пирамиду 


По определению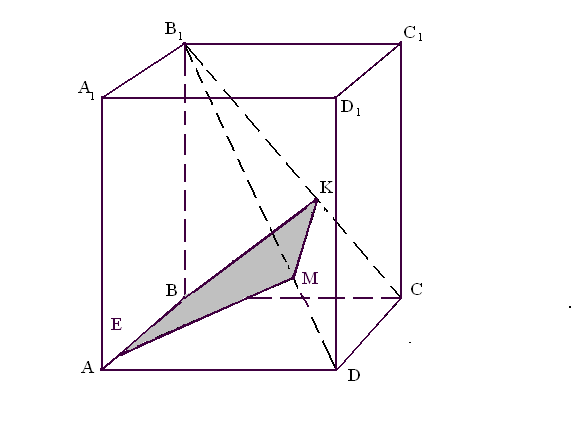
Решение.
Так как в основании призмы лежит
 квадрат, то АВ=
квадрат, то АВ= . Из CB1В B1C=
. Из CB1В B1C= .
.
![]()

![]()

![]()
![]()
![]()
![]() Сделаем дополнительные построения BK B1C , KM AB, EM BK .
Сделаем дополнительные построения BK B1C , KM AB, EM BK .
![]()
![]()
![]()
![]() Так как KM AB DC , то EM MK (EM перпендикуляр к плоскости DВ1C). Легко видеть, что EM – общий перпендикуляр к скрещивающимся прямым АB и B1D, причём EM= BK. Площадь треугольника BB1C S BB1C =
Так как KM AB DC , то EM MK (EM перпендикуляр к плоскости DВ1C). Легко видеть, что EM – общий перпендикуляр к скрещивающимся прямым АB и B1D, причём EM= BK. Площадь треугольника BB1C S BB1C = BB1 *BC =
BB1 *BC = BK*B1C Тогда BK=
BK*B1C Тогда BK= =
= =3.
=3.
EM=3.
Метод координат
Решение.
Введем прямоугольную систему координат как показано на рисунке.
A(0;0;0) B(0; ;0) C(
;0) C( ;0) D(
;0) D( 0;0)
0;0)
 (0;0;3
(0;0;3 )
)  (0;
(0; ;3
;3 )
)  ;
; )
)  (
( 0;
0; )
)
Плоскость (А1ВС); ах+ву+сz=d
c=
a=0
(A1BC):  y+
y+ z=d
z=d
3y+z=3
ñ (0 ;3 ;1) вектор нормали к(АВС)
 ‖‖
‖‖ 
F(0;3k;k)
Прямая (АВ)  =
= =
= ;
;
 =
= =;
=;


m=0,9.
;
;
 =
=







 Боковое ребро
Боковое ребро  см. Найти расстояние между стороной основания и диагональю, не имеющей с ней общих точек.
см. Найти расстояние между стороной основания и диагональю, не имеющей с ней общих точек.
 - В1С.
- В1С.
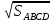 =
=  cм
cм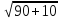 =10= В1С
=10= В1С 







 квадрат, то АВ=
квадрат, то АВ= . Из CB1В B1C=
. Из CB1В B1C= .
.





















