Мир правильных
многогранников.
Выполнила
Рудник Ольга Анатольевна
Учитель математики
МОШ I-III ступеней №53

- Многогранник - это тело, поверхность которого состоит из конечного числа плоских многоугольников.
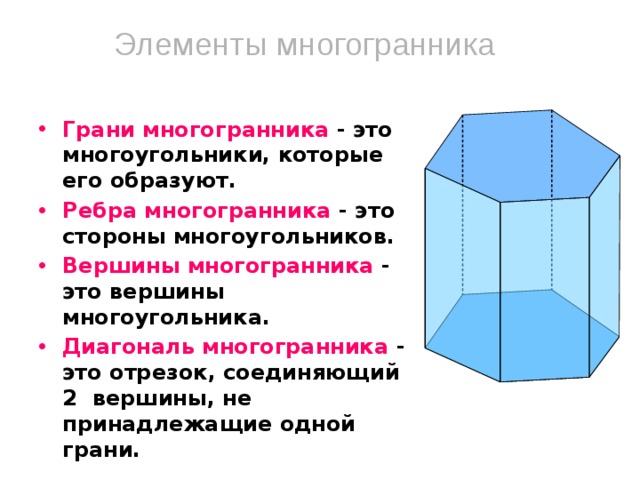
Элементы многогранника
- Грани многогранника - это многоугольники, которые его образуют.
- Ребра многогранника - это стороны многоугольников.
- Вершины многогранника - это вершины многоугольника.
- Диагональ многогранника - это отрезок, соединяющий 2 вершины, не принадлежащие одной грани.
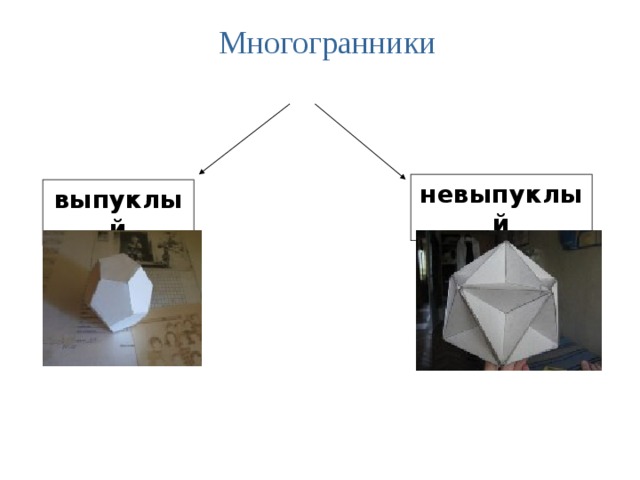
Многогранники
невыпуклый
выпуклый
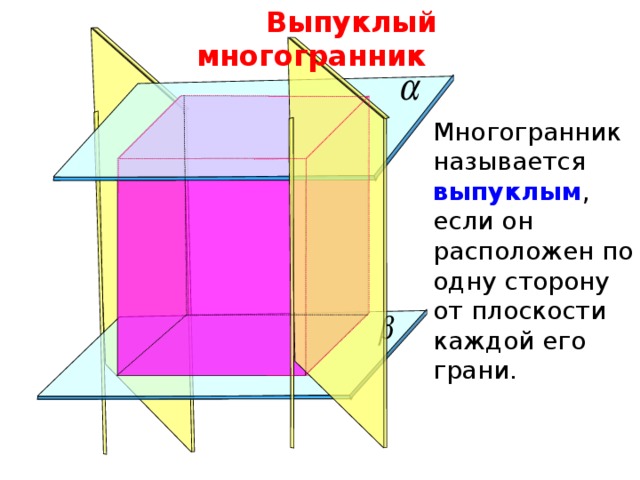
Выпуклый многогранник
Многогранник называется выпуклым , если он расположен по одну сторону от плоскости каждой его грани.
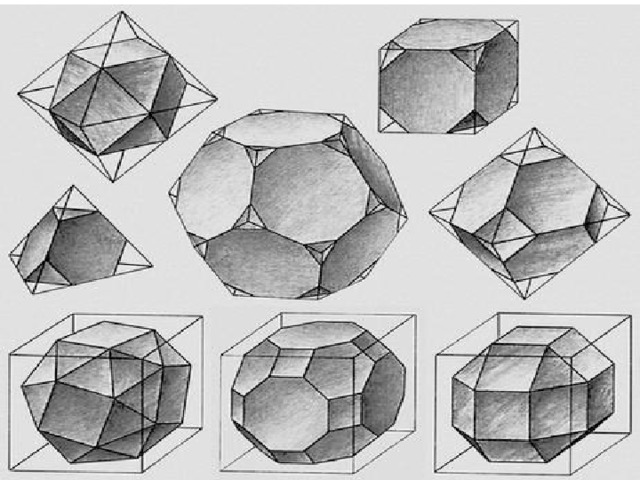
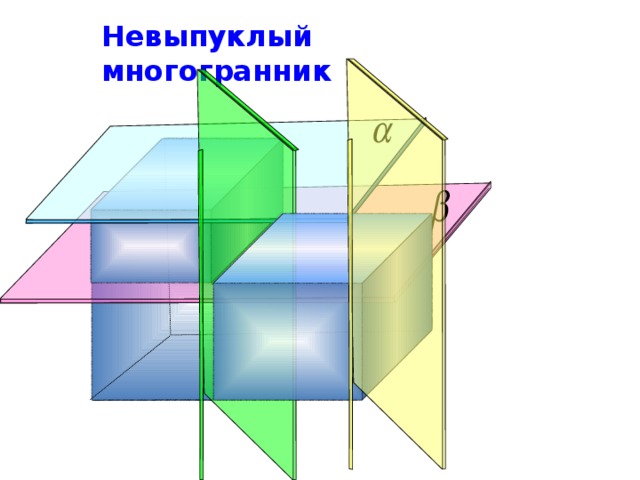
Невыпуклый многогранник
Г.В. Дорофеев, Л.Г. Петерсон, 6 класс (часть 3). № 742(а)
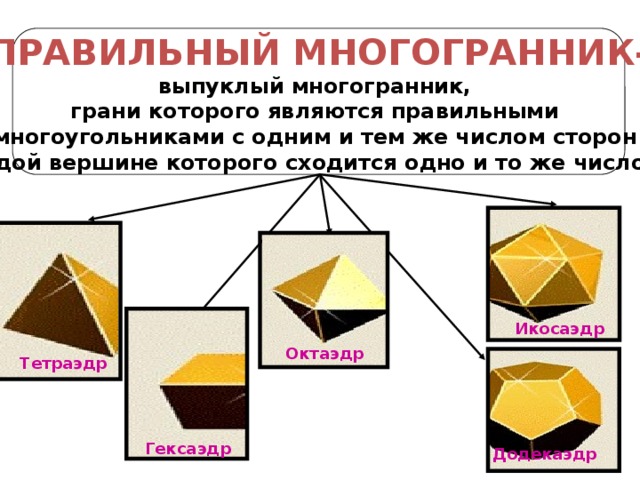
ПРАВИЛЬНЫЙ МНОГОГРАННИК-
выпуклый многогранник,
грани которого являются правильными
многоугольниками с одним и тем же числом сторон
и в каждой вершине которого сходится одно и то же число ребер.
Икосаэдр
Октаэдр
Тетраэдр
Гексаэдр
Додекаэдр
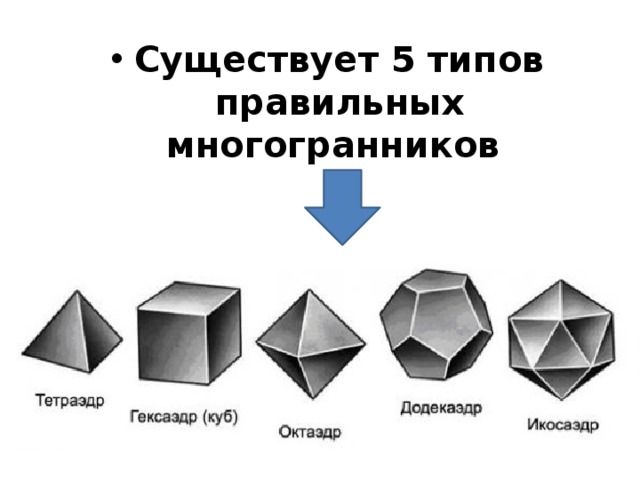
- Существует 5 типов правильных многогранников

- Тетраэдр - это треугольная пирамида, гранями которой являются треугольники

Основные формулы для тетраэдра
Определение:
- а – ребро,
- V-объем,
- S-площадь боковой поверхности,
- R-радиус описанной сферы,
- r- радиус вписанной сферы,
- H- высота.

- Октаэдр - это многогранник, гранями которого являются правильные треугольники и в каждой вершине сходится 4 грани.
Правильная форма алмаза – октаэдр

Основные формулы для октаэдра
Определение:
- а – ребро,
- V-объем,
- S-площадь боковой поверхности,
- R-радиус описанной сферы,
- r- радиус вписанной сферы,

- Гексаэдр (куб) - это многогранник, в каждой вершине которого сходится 3 квадрата.

Основные формулы для гексаэдра
Определение:
- а – ребро,
- V-объем,
- S-площадь боковой поверхности,
- R-радиус описанной сферы,
- r- радиус вписанной сферы,
- H- высота.

- Додекаэдр - это многогранник, в каждой вершине которого сходится 3 правильных многоугольника.

Основные формулы для додекаэдра
Определение:
- а – ребро,
- V-объем,
- S-площадь боковой поверхности,
- R-радиус описанной сферы,
- r- радиус вписанной сферы,
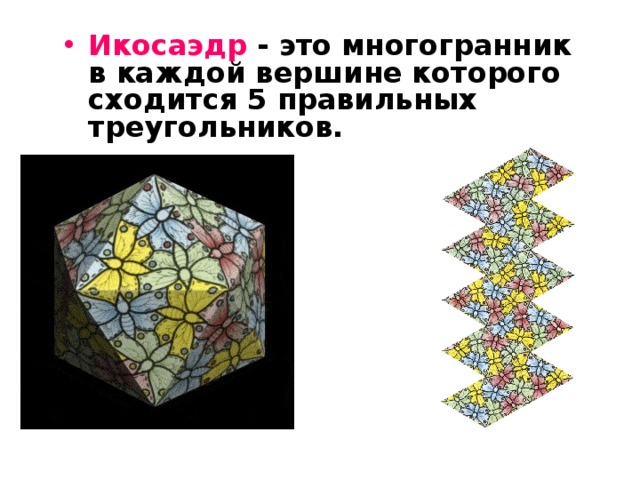
- Икосаэдр - это многогранник в каждой вершине которого сходится 5 правильных треугольников.

Названия многогранников
пришли из Древней Греции,
в них указывается число граней:
«эдра» грань;
«тетра» 4;
«гекса» 6;
«окта» 8;
«икоса» 20;
«додека» 12.

Правильные многогранники в философской картине мира Платона
Платон считал, что мир строится из четырёх «стихий» – огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.
Тетраэдр олицетворял огонь , поскольку его вершина устремлена вверх, как у разгоревшегося пламени.
Икосаэдр – как самый обтекаемый – воду .
Куб – самая устойчивая из фигур – землю .
Октаэдр – воздух .
В наше время эту систему можно сравнить с четырьмя состояниями вещества – твёрдым, жидким, газообразным и пламенным.
Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.
Это была одна из первых попыток ввести в науку идею систематизации.

тетраэдр
огонь
икосаэдр
вода
октаэдр
воздух
гексаэдр
земля
додекаэдр
вселенная

« Космический кубок» Кеплера
Кеплер предположил, что существует связь между пятью правильными многогранниками и шестью открытыми к тому времени планетами Солнечной системы.
Модель Солнечной
системы И. Кеплера

Икосаэдро-додекаэдровая
структура Земли
Идеи Платона и Кеплера о связи правильных многогранников с гармоничным устройством мира и в наше время нашли своё продолжение в интересной научной гипотезе, которую в начале 80-х гг. высказали московские инженеры В. Макаров и В. Морозов. Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете.
Икосаэдро-
додекаэдровая
структура Земли
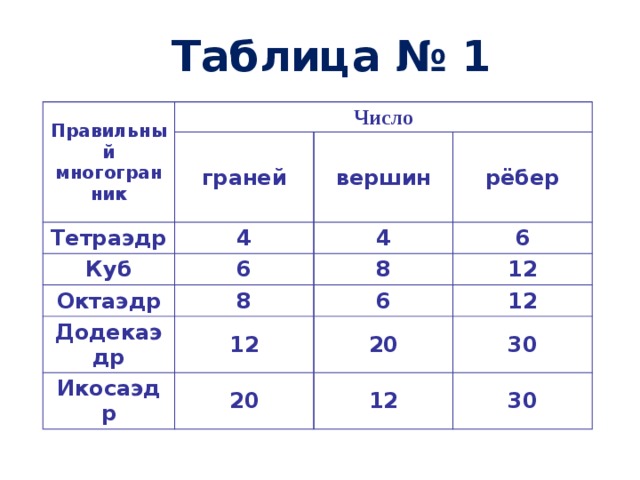
Таблица № 1
Правильный многогранник
Число
граней
Тетраэдр
4
вершин
Куб
6
рёбер
Октаэдр
4
8
6
Додекаэдр
8
12
12
6
Икосаэдр
12
20
20
30
12
30
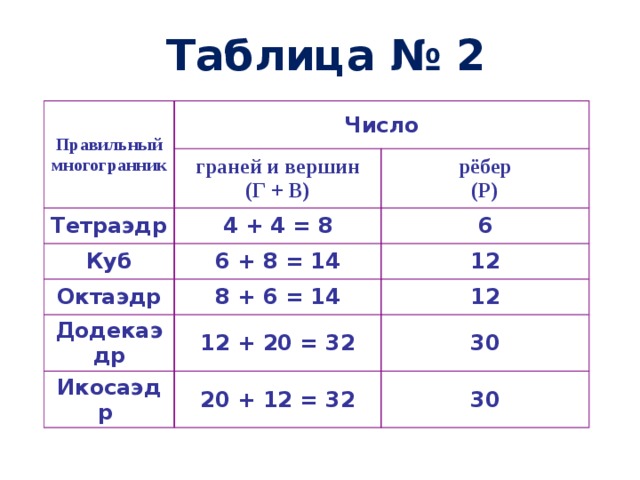
Таблица № 2
Правильный многогранник
Число
граней и вершин
Тетраэдр
(Г + В)
4 + 4 = 8
Куб
рёбер
Октаэдр
6 + 8 = 14
6
(Р)
8 + 6 = 14
Додекаэдр
12
12
12 + 20 = 32
Икосаэдр
20 + 12 = 32
30
30

Формула Эйлера
Сумма числа граней и вершин любого многогранника
равна числу рёбер, увеличенному на 2.
Г + В = Р + 2
Число граней плюс число вершин минус число рёбер
в любом многограннике равно 2.
Г + В Р = 2

- Французский математик Пуансо в 1810 году построил четыре правильных звездчатых многогранника: малый звездчатый додекаэдр, большой звездчатый додекаэдр, большой додекаэдр и большой икосаэдр.
И. Кеплер (1571 – 1630 гг.).
- В 1812 году французский математик О. Коши
доказал, что кроме пяти «платоновых тел» и
четырех «тел Пуансо» больше нет правильных многогранников.

Малый звездчатый
додекаэдр
Большой звездчатый
додекаэдр
Большой икосаэдр
Большой додекаэдр

Строение молекулы
метана .

Вирус полиомиелита имеет
форму додекаэдра.
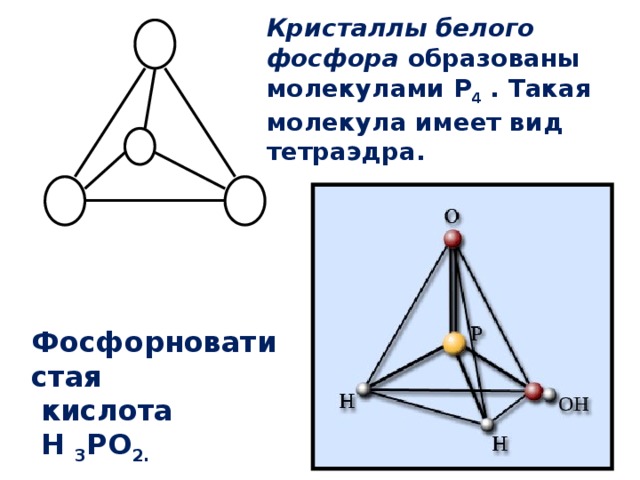
Кристаллы белого фосфора образованы молекулами Р 4 . Такая молекула имеет вид тетраэдра.
Фосфорноватистая
кислота
Н 3 РО 2.

Правильные многогранники и природа
Правильные многогранники встречаются в живой природе. Например, скелет одноклеточного организма феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр
Феодария
(Circjgjnia icosahtdra)

Леонардо да Винчи любил изготовлять из дерева каркасы правильных многогранников и преподносить их в виде подарка различным знаменитостям.

« Тайная вечеря»
Сальвадор Дали

Заключение
Высшее назначение математики- находить порядок в хаосе, который нас окружает Норберт Винер