Презентация "В мире многогранников"

В мире многогранников.

Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук". Л. Кэрролл

Определение

Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон.

Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер.

Выпуклый многогранник называется правильным, если в каждой вершине многогранника сходится одно и то же число ребер.

Тела

Форма грани

количество

Тетраэдр

Граней

Куб

(Г)

Вершин

Октаэдр

В+Г-Р

(В)

Ребер

Додекаэдр

(Р)

Икосаэдр

Тетраэдр.

Составлен из четырех равносторонних треугольников. Каждая вершина является вершиной трех треугольников.

Куб или гексаэдр.

Составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов.

Октаэдр.

Составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников.

Додекаэдр.

Составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников.

Икосаэдр.

Составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников.

Проверь таблицу!

Тела

Форма грани

количество

Тетраэдр

Граней

Правильный треугольник

Куб

(Г)

Вершин

4

Квадрат

Октаэдр

(В)

Ребер

В+Г-Р

4

6

Додекаэдр

Правильный треугольник

8

(Р)

6

8

Правильный треугольник

Икосаэдр

12

6

12

Правильный пятиугольник

20

12

20

30

12

30

Тела

Форма грани

Тетраэдр

количество

Граней

Правильный треугольник

Куб

Вершин

(Г)

Квадрат

4

Октаэдр

В+Г-Р

Ребер

4

6

(В)

Правильный треугольник

Додекаэдр

(Р)

8

6

Икосаэдр

8

Правильный треугольник

4+4-6=2

12

6

12

Правильный пятиугольник

6+8-12=2

20

12

20

30

8+6-12=2

12

12+20-30=2

30

20+12-30=2

Теорема Эйлера.

Пусть В  – число вершин выпуклого многогранника, Р – число его ребер и Г – число граней. Тогда верно равенство В+Г-Р=2.

Это интересно!

«эдра» - грань

тетраэдр

«тетра» - 4

гексаэдр

«гекса» - 6

четырехгранник

октаэдр

шестигранник

додекаэдр

«окта» - 8

«додека» - 12

восьмигранник

икосаэдр

двенадцатигранник

«икоса» - 20

двадцатигранник

В своих философских теориях

правильные многогранники использовали:

Кеплер

Архимед

Евклид

Пифагор

Платон

Древнегреческий ученый и философ Платон считал, что правильные многогранники олицетворяют сущность природы. Поэтому эти многогранники называют Платоновыми телами.

Тетраэдр олицетворял огонь, так как его вершина устремлена вверх, как у разгоревшегося пламени.

Куб, как самая устойчивая из фигур символизировал землю.

Икосаэдр, как самый обтекаемый – воду.

Октаэдр олицетворял воздух.

Додекаэдр символизировал

весь мир. .

Многогранники в природе.

Молекула метана имеет форму правильного тетраэдра. Этот факт подтверждается фотографиями, полученными при помощи электронного микроскопа.

Многогранники в природе.

Феодарии – одноклеточные организмы, форма которых точно передает икосаэдр.

Многогранники в природе.

В центре внимания биологов, в их спорах относительно формы вирусов, оказался икосаэдр.

Вирус полиомиелита

Многогранники в природе.

Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников. Так, куб передает форму кристаллов поваренной соли,

монокристалл алюминиево-калиевых квасцов имеет форму октаэдра, кристалл сернистого колчедана имеет форму додекаэдра, сурьмянистый сернокислый натрий - тетраэдра, бор – икосаэдра.

Правильные многогранники - самые выгодные фигуры. И природа этим широко пользуется.

Базальтовые столбы

Многогранники в живописи.

Сальвадор Дали "Тайная вечеря"

Многогранники в живописи.

Альбрехт Дюрер

«Меланхолия»

Мауриц Эшер

«Контраст»

«Рептилии»

«Звезды»

Многогранники в архитектуре .

Часовня академии ВВС. Колорадо, США.

Эспланада. Сингапур.

Муниципальное здание. Темпе, Аризона, США.

Концертный зал имени Уолта Диснея . Лос-Анджелес, Калифорния, США.

Национальная библиотека. Минск, Белоруссия.

Хабитат 67. Канада.

Площадь Федерации .

Мельбурн, Австралия.

Многогранники в архитектуре Воронежа.

Многогранники и высокая мода.

Конкурс «Лучший дизайнер»

Итоги конкурса.

Первое место – Андреева Светлана

Второе место – Бабенко Алина

Третье место – Юркаева Анастасия

Колган Татьяна

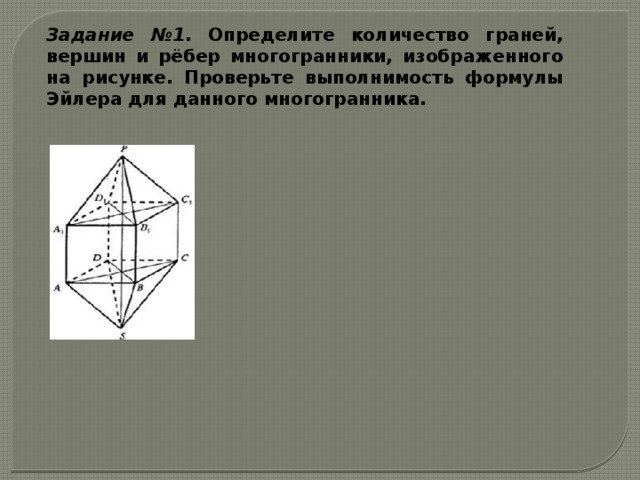
Задание №1 . Определите количество граней, вершин и рёбер многогранники, изображенного на рисунке. Проверьте выполнимость формулы Эйлера для данного многогранника.

В=10, Г=12, Р=20

В+Г-Р=10+12-20=2.

Задание № 3 . Определить разверткой какого многогранника, является каждая из данных разверток.