Презентация по теме "Софизмы"

Софизмы

История софизма

Софизм

– слово греческого происхождения, в

переводе означающее хитроумную выдумку, ухищрение, головоломку или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям. Каким бы ни был софизм, он всегда содержит одну или несколько замаскированных ошибок. Систематический анализ софизмов был дан впервые Аристотелем   (384-322 до н. э.) в особом трактате, в котором все ошибки разделяются на два класса: "неправильности речи" и ошибки "вне речи", т.е. в мышлении.

Пример 1.

Докажем, что 1 руб. = 10 000 коп.

Возьмём верное равенство:

1 руб = 100 коп

Возведём его по частям в квадрат.

1 руб·1 руб = 100 коп ·100 коп .

Мы получим: 1 руб = 100 00 коп

Вопрос:

В чём ошибка?

Ответ: Возведение в квадрат величин не имеет смысла. В квадрат возводятся только числа.

Пример 2.

Докажем, что 5 = 6

Возьмём верное равенство:

35 + 10 – 45 = 42 + 12 – 54 .

Вынесем общие множители левой и правой частей за скобки. Получим:

5 (7 + 2 – 9) = 6 (7 + 2 – 9) .

Разделим обе части этого равенства на общий множитель, который заключён в скобки.

Получаем 5 = 6 .

************************************************************************************

Вопрос:

В чём ошибка?

Ответ: Общий множитель (7 + 2 – 9) равен 0 , а делить на 0 нельзя.

Пример 3.

Докажем, что 4 = 5

Возьмём верное равенство:

4:4= 5:5 .

Вынесем общие множители левой и правой частей за скобки. Получим:

4 (1:1) = 5 (1:1) .

Разделим обе части этого равенства на общий множитель, который заключён в скобки.

Получаем 4 = 5 .

************************************************************************************

Вопрос:

В чём ошибка?

Ответ: Ошибка сделана при вынесении общих множителей 4 из левой части и 5 из правой. Так выносить за скобки нельзя! Действительно, 4:4=1:1, но 4:4 ≠ 4(1:1). Неверно переносить распределительный закон умножения на деление !

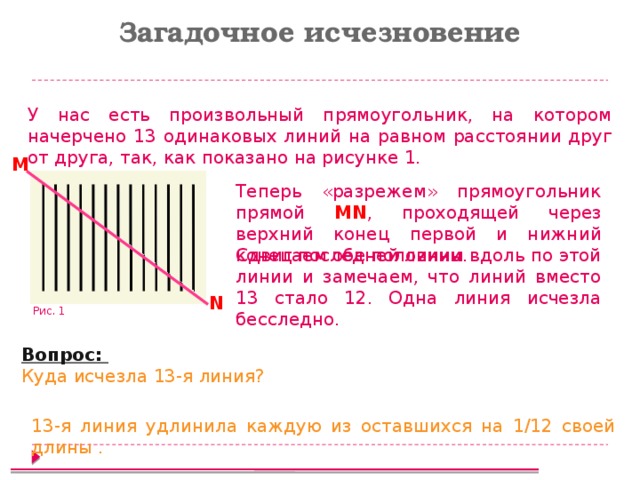
Загадочное исчезновение

У нас есть произвольный прямоугольник, на котором начерчено 13 одинаковых линий на равном расстоянии друг от друга, так, как показано на рисунке 1.

M

Теперь «разрежем» прямоугольник прямой MN , проходящей через верхний конец первой и нижний конец последней линии.

Сдвигаем обе половины вдоль по этой линии и замечаем, что линий вместо 13 стало 12. Одна линия исчезла бесследно.

N

Рис. 1

Вопрос:

Куда исчезла 13-я линия?

13-я линия удлинила каждую из оставшихся на 1/12 своей длины .

6

Задача

Докажем, что 3 раза по 2 будет не 6, а 4.

Возьмем спичку.

Разделим ее пополам. Получили 1 раз по 2.

Разделим одну часть еще пополам. Получим второй раз по два.

Разделим еще раз одну часть пополам. Получим третий раз по два.

Итого, получили 4.

В чем ошибка?

СОФИЗМ

• «Для того чтобы видеть, вовсе необязательно иметь глаза, ведь без правого глаза мы видим, без левого тоже видим; кроме правого и левого, других глаз у нас нет; поэтому ясно, что глаза не являются необходимыми для зрения».

Софизм учебы

• Чем больше учишься, тем больше знаешь.
• Чем больше знаешь, тем больше забываешь.
• Чем больше забываешь, тем меньше знаешь.
• Чем меньше знаешь, тем меньше забываешь.
• Но чем меньше забываешь, тем больше знаешь.
• Так для чего учиться?