Россия, Республика Марий Эл, Оршанский район
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 17.10.2021 01:16
Софронова Наталия Андреевна
Учитель математики
70 лет
92 457
167 
Местоположение
Специализация
Применение векторов к решению задач
Категория:
Математика
27.04.2017 21:35
Просмотр содержимого документа
«Применение векторов к решению задач»
Применение векторов к решению задач
К учебнику Геометрия 7-9,
автор Л.С.Атанасян и др.
Автор: Софронова Наталия Андреевна,
учитель математики высшей категории
МОУ «Упшинская основная общеобразовательная школа»
Оршанского района Республики Марий Эл
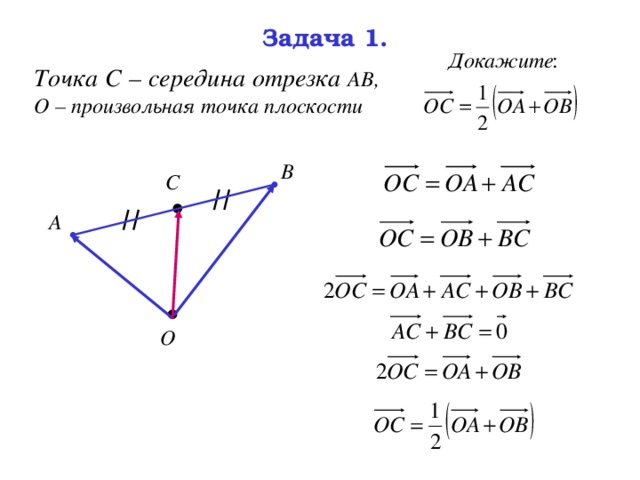
Задача 1.
Точка С – середина отрезка АВ, О – произвольная точка плоскости
B
C
A
O
Задача 2.
Доказать, что прямая, проведенная через середины оснований трапеции проходит через точку пересечения продолжений боковых сторон.
O
С
В
М
А
N
D
Задача 3.
В треугольнике АВС В 1 - середина стороны АС, точка А 1 лежит на стороне ВС так, что ВА 1 : А 1 С = 1 : 2. Используя векторы, докажите, что середина ВВ 1 лежит на прямой АА 1.
Доказать: О є АА 1
О – середина ВВ 1
В
А 1
О
А
С
В 1
Задача 3 (продолжение).
О – середина ВВ 1
Доказать: О є АА 1
В
А 1
О
лежат на одной прямой,
О є АА 1
А
С
В 1
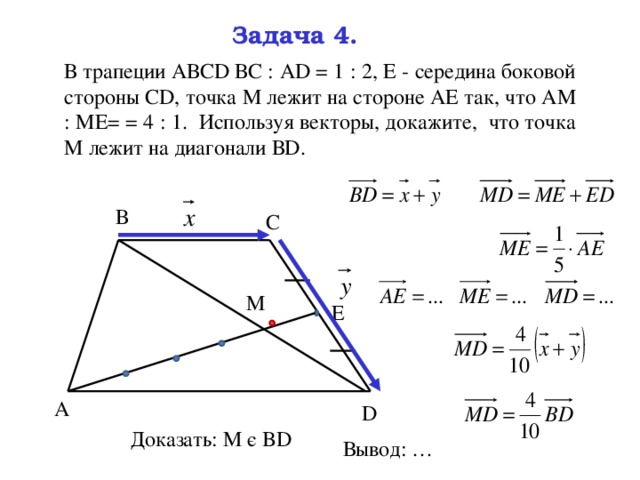
Задача 4.
В трапеции АВСD ВС : АD = 1 : 2, Е - середина боковой стороны СD, точка М лежит на стороне АЕ так, что АМ : МЕ= = 4 : 1. Используя векторы, докажите, что точка М лежит на диагонали ВD.
В
С
М
Е
А
D
Доказать: М є BD
Вывод: …
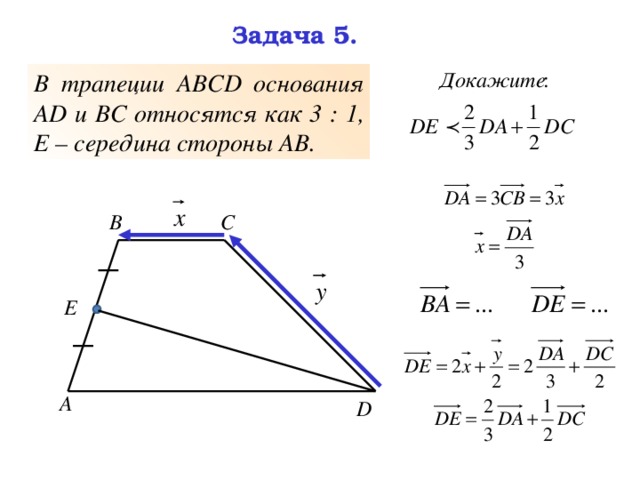
Задача 5.
В трапеции АВСD основания АD и ВС относятся как 3 : 1, Е – середина стороны АВ.
B
C
E
A
D
Задача 5 (продолжение).
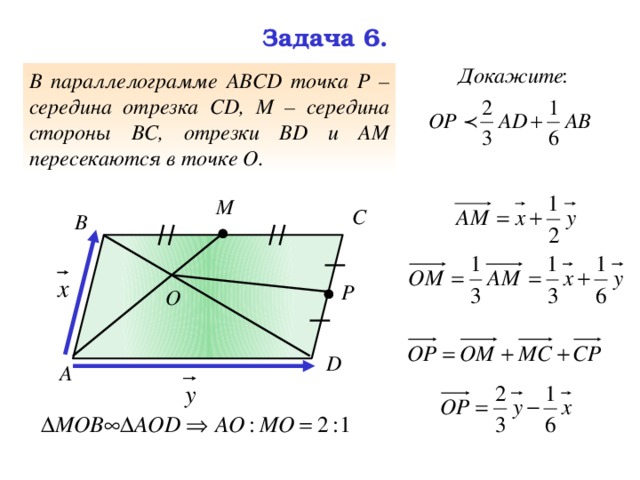
Задача 6.
В параллелограмме АВСD точка Р – середина отрезка СD, М – середина стороны ВС, отрезки ВD и АМ пересекаются в точке О.
M
C
B
P
O
D
A
Задача 6 (продолжение).
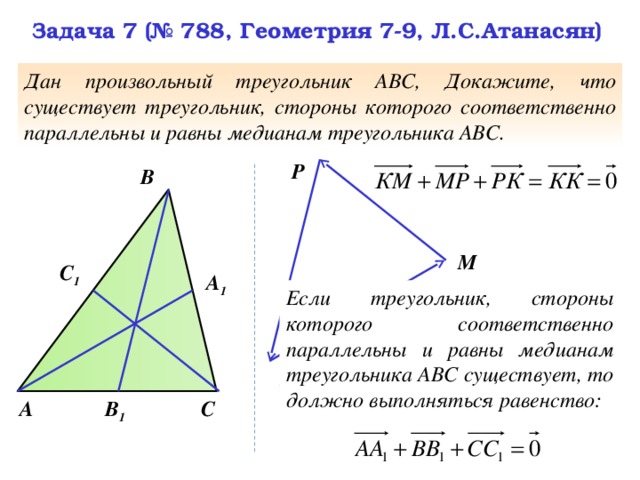
Задача 7 (№ 788, Геометрия 7-9, Л.С.Атанасян)
Дан произвольный треугольник АВС, Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника АВС.
Р
В
М
С 1
А 1
Если треугольник, стороны которого соответственно параллельны и равны медианам треугольника АВС существует, то должно выполняться равенство:
К
В 1
С
А
В
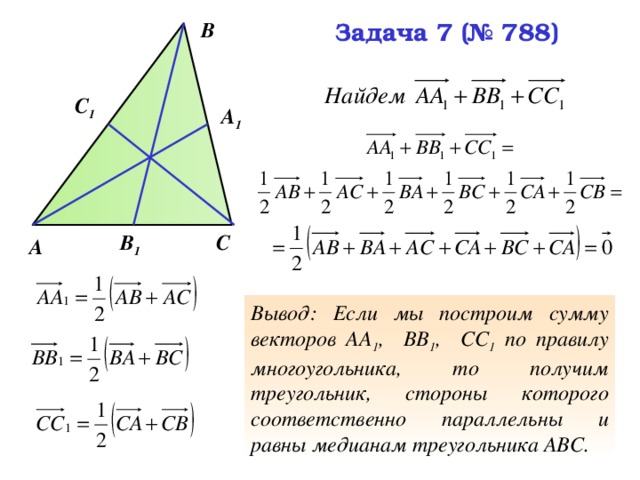
Задача 7 (№ 788)
С 1
А 1
В 1
С
А
Вывод: Если мы построим сумму векторов АА 1 , ВВ 1 , СС 1 по правилу многоугольника, то получим треугольник, стороны которого соответственно параллельны и равны медианам треугольника АВС.
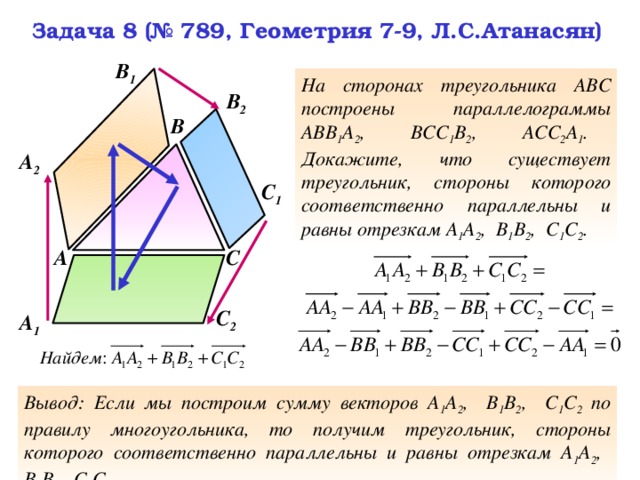
Задача 8 (№ 789, Геометрия 7-9, Л.С.Атанасян)
В 1
На сторонах треугольника АВС построены параллелограммы АВВ 1 А 2 , ВСС 1 В 2 , АСС 2 А 1 . Докажите, что существует треугольник, стороны которого соответственно параллельны и равны отрезкам А 1 А 2 , В 1 В 2 , С 1 С 2 .
В 2
В
А 2
С 1
С
А
С 2
А 1
Вывод: Если мы построим сумму векторов А 1 А 2 , В 1 В 2 , С 1 С 2 по правилу многоугольника, то получим треугольник, стороны которого соответственно параллельны и равны отрезкам А 1 А 2 , В 1 В 2 , С 1 С 2 .
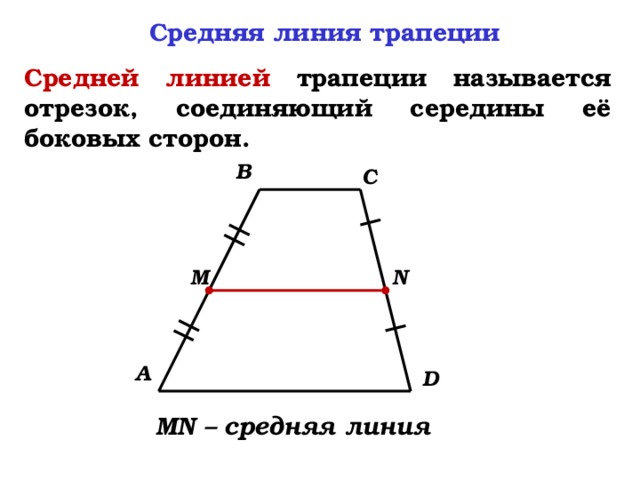
Средняя линия трапеции
Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
В
С
N
M
А
D
MN – средняя линия
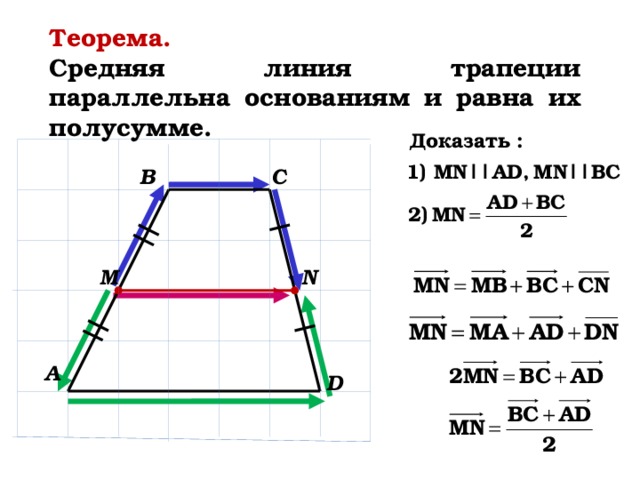
Теорема.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
С
В
M
N
А
D
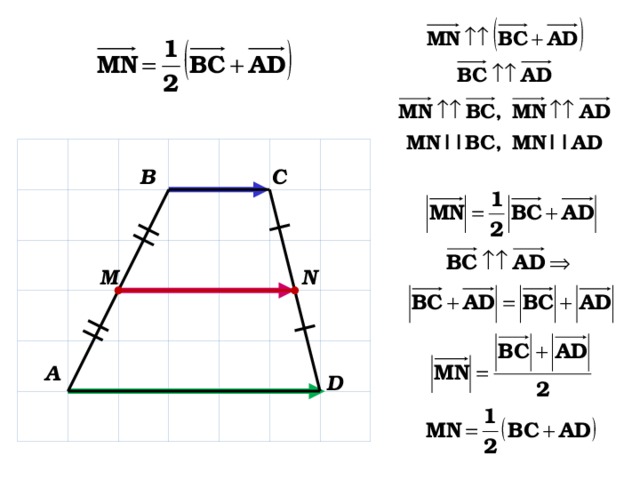
В
С
M
N
А
D
.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
