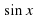СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Программа по алгебре и начала математического анализа. 8-11класс
Программа по алгебре и началу анализа. 8-11 класс
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ПУШКИНСКАЯ СРЕДНЯЯ ШКОЛА»
СОВЕТСКОГО РАЙОНА РЕСПУБЛИКИ КРЫМ
|
РАССМОТРЕНО на МО учителей естественно -математического цикла Протокол № от « ___ »_____________2016 г. Руководитель МО ____________ Смеянова Т.В. |
СОГЛАСОВАНО Заместитель директора по УВР МБОУ «Пушкинская СШ»
_____________ Завора А.В. « ____ »____________ 2016 г.
|
УТВЕРЖДАЮ Директор МБОУ «Пушкинская СШ» _________Глущенко В.Д. Приказ № ________ от «___» ________2016 г. |
РАБОЧАЯ ПРОГРАММА
ПО УЧЕБНОМУ ПРЕДМЕТУ «АЛГЕБРА» (базовый уровень)
|
(наименование учебного предмета/курса) 8 |
|
(классы)
|
Программу составила учитель __Мамбетова Венера Хайдаровна, _I-категории
(Ф.И.О., квалификационная категория учителя, составившего рабочую учебную программу)
с. Пушкино, 2016 г.
Пояснительная записка.
Данная рабочая программа разработана в соответствии с основными положениями Федерального государственного образовательного стандарта и требованиями Примерной образовательной программы основного общего образования, с учетом основных идей и положений Программы развития и формирования универсальных учебных действий и ориентирована на использование учебно-методического комплекта:
- Программы общеобразовательных учреждений. Алгебра. 7-9 классы / Ю.Н.Макарычев, Н.Г.Миндюк; составительН.Г.Миндюк – М.: Просвещение, 2014;
- Государственный стандарт основного общего образования по математике.
Программа соответствует учебнику «Алгебра. 8 класс» / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Теляковского. М.: Просвещение, 2014.
Примерная программа конкретизирует содержание предметных тем образовательного стандарта и даёт примерное распределение учебных часов по разделам курса.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса. Содержание программы направлено на освоение учащимися знаний, умений и навыков на базовом уровне, что соответствует Образовательной программе школы. Она включает все темы, предусмотренные федеральным компонентом государственного образовательного стандарта основного общего образования по математике.
Место предмета в базисном учебном плане.
Согласно действующему учебному плану рабочая программа предусматривает обучение в объеме 105 часов.из них3ч. резерв. (3 часа в неделю)
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
- овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
- интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
- формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
- воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ
ИЗУЧЕНИЯ КУРСА АЛГЕБРЫ В 8 КЛАССЕ.
В результате изучения алгебры ученик должен
- знать/понимать
- существо понятия математического доказательства; примеры доказательств;
- существо понятия алгоритма; примеры алгоритмов;
- как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
- как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
Просмотр содержимого документа
«АЛГЕБРА 11кл.»
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ПУШКИНСКАЯ СРЕДНЯЯ ШКОЛА»
СОВЕТСКОГО РАЙОНА РЕСПУБЛИКИ КРЫМ
| РАССМОТРЕНО на МО учителей естественно-математического цикла Протокол № от « ___ »_____________2016 г. Руководитель МО ____________ Смеянова Т.В. | СОГЛАСОВАНО Заместитель директора по УВР МБОУ «Пушкинская СШ»
_____________ Завора А.В. | УТВЕРЖДАЮ Директор МБОУ «Пушкинская СШ» ___________Глущенко В.Д. Приказ № ________ от «___» __________2016 г. |
РАБОЧАЯ ПРОГРАММА
ПО УЧЕБНОМУ ПРЕДМЕТУ «АЛГЕБРА И НАЧАЛА АНАЛИЗА» (базовый уровень)
| (наименование учебного предмета/курса) 11 |
| (классы) |
Программу составила учитель __Мамбетова Венера Хайдаровна, _I-категории
(Ф.И.О., квалификационная категория учителя, составившего рабочую учебную программу)
с. Пушкино, 2016г.
Пояснительная записка
Рабочая программа по алгебре и началам анализа составлена на основе нормативных правовых документов:
Федерального закона Российской Федерации «Об образовании в Российской Федерации» (№ 273-ФЗ от 29.12.2012).
Приказа Минобразования России от 09.03.2004г. № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального, основного общего и среднего (полного) общего образования»
Приказа Минобрнауки России от 20.08.2008г. № 241 «О внесении изменений в федеральный базисный учебный план и примерные учебные планы для образовательных учреждений РФ, реализующих программы общего образования, утвержденные приказом министерства образования РФ от 09.03.2004г. №1312 «Об утверждении федерального базисного учебного плана и примерных учебных плановдля образовательных учреждений РФ, реализующих программы общего образования»
Приказа Минобрнауки России от 06.10.2009г. № 373 ««Об утверждении и введении в действие федерального государственного образовательного стандарта начального общего образования»
Стандарт основного общего образования по математике //Сборник нормативно- правовых документов и методических материалов, Москва: «Вентана-Граф», 2008.
Алгебра и начала математического анализа 10 – 11 классы. Программы общеобразовательных учреждений (составитель Т.А. Бурмистрова). М.: «Просвещение» 2009.
Основными учебными пособиями для обучающихся являются:
1. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс: учебник для общеобразовательных организаций: базовый и углубленный уровни / [С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин]. — М.: Просвещение, 2014. – 464с.
2. Алгебра и начала математического анализа. Дидактические материалы / М.К.Потапов. М.: Просвещение, 2010;
Программа по математике 11 класс рассчитана на 3 часа алгебры в неделю (всего 102 часа из них 3ч. резервных)
Планируемые результаты освоения учебного предмета
В результате изучения курса математики 11 класса обучающиеся должны:
знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира.
Алгебра
уметь
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.
Начала математического анализа
уметь
вычислять производные и первообразные элементарных функций, используя справочные материалы;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
вычислять в простейших случаях площади с использованием первообразной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
Уравнения и неравенства
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
составлять уравнения и неравенства по условию задачи;
использовать для приближенного решения уравнений и неравенств графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
построения и исследования простейших математических моделей.
Элементы комбинаторики, статистики и теории вероятностей
уметь
решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул;
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
анализа реальных числовых данных, представленных в виде диаграмм, графиков;
анализа информации статистического характера.
Содержание учебного предмета
Функции и график 2. 1. Функции и их графики. Предел функции и непрерывность. Обратные
функции. (15 часов, из них 1час контрольная работа).
Элементарные функции и их свойства. Основные способы преобразования графиков. Понятие предела функции. Односторонние пределы. Свойства пределов функций. Понятие непрерывности функции. Непрерывность элементарных функций. Разрывные функции. Понятие обратной функции. Взаимообратные функции.
2. Производная функции и ее применение (22 часа, из них 2часа контрольные работы).
Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков. Производные обратной функции и композиции данной функции с линейной. Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах. Нахождение скорости для процесса, заданного формулой или графиком. Вторая производная и ее физический смысл.
4. Первообразная и интеграл (10 часов, из них 1час контрольная работа).
Понятие об определенном интеграле как площади криволинейной трапеции. Первообразная. Формула Ньютона-Лейбница. Примеры применения интеграла в физике и геометрии.
5. Уравнения. Неравенства. Системы (38 часов, из них 3 часа контрольных работ).
Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение простейших систем уравнений с двумя неизвестными. Решение систем неравенств с одной переменной.
Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.
Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
6. Элементы комбинаторики, теории вероятности, статистики Повторение курса алгебры и математического анализа (13 часов, из них 1 час контрольная работа).
В связи с необходимостью провести обобщающее повторение материала 10 класса целесообразным является введение раздела «Повторение» (4 часа) в начале учебного года.
(Курсивом выделен материал, который подлежит изучению, но не включается в Требования к уровню подготовки выпускников)
Тематическое планирование по алгебре и началам математического анализа
|
№ |
Тема |
| |
| Кол. часов | Кол-во контрольных работ | ||
| 1 | Повторение за курс 10кл. | 4 | |
| 2 | Функции и их графики | 9 | 1 |
| 3 | Предел функции и непрерывность | 4 | |
| 4 | Обратные функции | 2 | |
| 5 | Производная | 8 | 1 |
| 6 | Применение производной | 14 | 1 |
| 7 | Первообразная и интеграл | 10 | 1 |
| 8 | Уравнения. Неравенства. Системы | 38 | 3 |
| 9 | Повторение. Итоговая контрольная работа | 13 | 1 |
|
| Итого | 102 часа | 8 |
Календарно-тематическое планирование
Алгебра и начала математического анализа 11 класс
Количество часов: 102 часа из них 3ч. резервных, 3 часа в неделю.
Алгебра и начала математического анализа: учеб. для 11 кл. общеобразоват. организаций: базовый и профильный уровни /С.М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. -М.: Просвещение, 2014.
|
№ |
Тема урока |
Кол. часов | Дата |
Повторение | |
| По плану | По факту
| ||||
|
| Повторение | 4 |
|
|
|
| 1 | Корень п-ой степени. Степень с рациональным показателем и ее свойства. | 1 |
|
| Свойства степеней |
| 2 | Решение логарифмических уравнений и неравенств. | 1 |
|
| Свойства логарифма |
| 3 | Решение тригонометрических уравнений. | 1 |
|
| Формулы корней тригономе- трических уравнений. |
| 4 | Входной контроль | 1 |
|
|
|
|
| Функции и их графики | 15 |
|
|
|
| 5 | Элементарные функции | 1 |
|
| Монотонность функции. |
| 6 | Область определения и область значения функции. Ограниченность функции | 1 |
|
| Нахождение значения функции в точке. |
| 7 | Четность, нечетность, периодичность функций | 1 |
|
| Формулы движения. |
| 8 | Четность, нечетность, периодичность функций | 1 |
|
| Средняя скорость движения |
| 9 | Промежутки возрастания, убывания, знакопостоянства и нули функции | 1 |
|
| Свойства ригонометричес- ких функций. |
| 10 | Исследование функций и построение их графиков элементарными методами | 1 |
|
| Возрастание и убывание функции. |
| 11 | Исследование функций и построение их графиков элементарными методами | 1 |
|
| Элементарные функции и их графики. Приращение функции. |
| 12 | Основные способы преобразования графиков | 1 |
|
| Область определения и область значения функции. |
| 13 | Понятие предела функции. Понятие непрерывности функции. | 1 |
|
| Теоремы о производной функции. |
| 14 | Односторонние пределы | 1 |
|
|
|
| 15 | Свойства пределов функций | 1 |
|
|
|
| 16 | Понятие непрерывности функции. | 1 |
|
|
|
| 17-18 | Понятие обратной функции | 2 |
|
|
|
| 19 | Контрольная работа №1 «Функции и их графики» | 1 |
|
| Решение неравенств |
|
| Производная | 8 |
|
|
|
| 20 | Понятие производной функции. Физический и геометрический смысл. |
|
|
| Метод интервалов. |
| 21 | Производная суммы. Производная разности. |
|
|
|
|
| 22,23 | Производная произведения. Производная частного | 2 |
|
| Алгоритм решения уравнений. |
| 24 | Производные элементарных функций | 1 |
|
| Действия с рациональны- ми числами. |
| 25,26 | Производная сложной функции | 2 |
|
| Возрастание и убывание функции. |
| 27 | Контрольная работа №2. «Производная» |
|
|
| Локальный экстремум. |
|
| Применение производной | 14 |
|
|
|
| 28,29 | Максимум и минимум функции | 2 |
|
| Производные элементарных функций |
| 30,31 | Уравнение касательной | 2 |
|
|
|
| 32 | Вторая производная и ее физический смысл | 1 |
|
|
|
| 33,34 | Возрастание и убывание функций | 2 |
|
| Производная суммы. Производная разности. |
| 35,36 | Экстремум функции с единственной критической точкой. | 2 |
|
| Критические точки. |
| 37,38 | Задачи на максимум и минимум. | 2 |
|
|
|
| 39,40 | Построение графиков функций с применением производной. | 2 |
|
| Производная сложной функции |
| 41 | Контрольная работа №3. «Применение производной» |
|
|
|
|
|
| Первообразная и интеграл | 10 |
|
|
|
| 42,43 | Первообразная. Таблица первообразных. | 2 |
|
| Общая схема исследования Функции. |
| 44,45 | Основное свойство первообразной. | 2 |
|
| Таблица производных. |
| 46 | Правила нахождения первообразной. | 1 |
|
| Теоремы о производных. |
| 47 | Примеры задач, которые приводят к пониманию интеграла. Определение интеграла. | 1 |
|
| Возрастание и убывание функции. |
| 48,49 | Формула Лейбница-Ньютона. | 2 |
|
| Площадь прямоугольника и трапеции. |
| 50 | Применение интеграла к вычислению площадей плоских фигур. | 1 |
|
| Графики элементарных функций. |
| 51 | Контрольная работа№4 | 1 |
|
| Таблица первообразных. |
|
| Уравнения. Неравенства. Системы | 38 |
|
|
|
| 52 | Равносильность уравнений и неравенств(4). Равносильные преобразования уравнений | 1 |
|
| Раскрытие скобок. |
| 53 | Равносильные преобразования уравнений | 1 |
|
| Формулы сокращенного умножения. |
| 54 | Равносильные преобразования неравенств | 1 |
|
| Правила нахождения первообразной. |
| 55 | Равносильные преобразования неравенств | 1 |
|
| Формула Лейбница-Ньютона. |
| 56 | Уравнения-следствия (7). Понятие уравнения-следствия | 1 |
|
| Решение уравнений. |
| 57 | Возведение уравнения в чётную степень | 1 |
|
| Решение тригонометричес-ких уравнений. |
| 58 | Возведение уравнения в чётную степень | 1 |
|
|
|
| 59 | Потенцирование логарифмических уравнений | 1 |
|
| Свойства логарифмов. |
| 60 | Другие преобразования, приводящие к уравнению-следствию | 1 |
|
| Показательные уравнения. |
| 61 | Применение нескольких преобразований, приводящих к уравнению-следствию | 1 |
|
| Свойства неравенств. |
| 62 | Применение нескольких преобразований, приводящих к уравнению-следствию | 1 |
|
|
|
| 63 | Равносильность уравнений и неравенств системам(9). Основные понятия | 1 |
|
| Свойства показ-ной функции |
| 64 | Решение уравнений с помощью систем | 1 |
|
|
|
| 65 | Решение уравнений с помощью систем | 1 |
|
| Свойства логариф-ой функции |
| 66 | Решение уравнений с помощью систем | 1 |
|
| Метод интервалов. |
| 67 | Решение уравнений с помощью систем | 1 |
|
|
|
| 68 | Решение неравенств с помощью систем | 1 |
|
|
|
| 69 | Решение неравенств с помощью систем | 1 |
|
| Алгоритм решение неравенств. |
| 70 | Решение неравенств с помощью систем | 1 |
|
|
|
| 71 | Решение неравенств с помощью систем | 1 |
|
| Действительные числа. |
| 72 | Равносильность уравнений на множествах(4). Основные понятия | 1 |
|
|
|
| 73 | Возведение уравнения в чётную степень | 1 |
|
|
|
| 74 | Возведение уравнения в чётную степень | 1 |
|
| Логарифмические уравнения. |
| 75 | Контрольная работа №5 | 1 |
|
| Таблица производных. |
| 76 | Равносильность неравенств на множествах(3). Основные понятия | 1 |
|
| Исследование функций. Построение графиков функций. |
| 77 | Возведение неравенств в чётную степень | 1 |
|
| Свойства степеней |
| 78 | Возведение неравенств в чётную степень | 1 |
|
| Свойства логарифма |
| 79 | Метод промежутков для уравнений и неравенств(4). Уравнения с модулями | 1 |
|
| Формулы корней тригономе- трических уравнений. |
| 80 | Неравенства с модулями | 1 |
|
|
|
| 81 | Метод интервалов для непрерывных функций | 1 |
|
|
|
| 82 | Контрольная работа №6 | 1 |
|
| Монотонность функции. |
| 83 | Системы уравнений с несколькими неизвестными(7). Равносильность систем | 1 |
|
| Нахождение значения функции в точке. |
| 84 | Равносильность систем | 1 |
|
| Формулы движения. |
| 85 | Система-следствие | 1 |
|
| Средняя скорость движения |
| 86 | Система-следствие | 1 |
|
| Свойства ригонометричес- ких функций. |
| 87 | Метод замены неизвестных | 1 |
|
| Возрастание и убывание функции. |
| 88 | Метод замены неизвестных | 1 |
|
| Элементарные функции и их графики. Приращение функции. |
| 89 | Контрольная работа №7
| 1 |
|
|
|
| | Повторение курса алгебры за 10-11 классы. |
13 |
|
|
|
| 90,91 | Тождественные преобразование выражений. | 2 |
|
|
|
| 92,93 | Функции, свойства и их графики. | 2 |
|
|
|
| 94,95 | Производная сложной, показательной, логарифмической и степенной функции.
| 2 |
|
|
|
| 96,97 | Показательные и логарифмические уравнения и неравенства | 2 |
|
|
|
| 98,99 | Тригонометрические уравнения и неравенства. | 2 |
|
|
|
| 100 | Свойства вероятностей | 1 |
|
|
|
| 101 | Итоговая контрольная работа | 1 |
|
|
|
| 102 | Итоговый урок | 1 |
|
|
|
10
Просмотр содержимого документа
«АЛГЕБРА 9КЛ.»
12
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ПУШКИНСКАЯ СРЕДНЯЯ ШКОЛА»
СОВЕТСКОГО РАЙОНА РЕСПУБЛИКИ КРЫМ
| РАССМОТРЕНО на МО учителей естественно-математического цикла Протокол № от « ___ »_____________2016 г. Руководитель МО ____________ Смеянова Т.В. | СОГЛАСОВАНО Заместитель директора по УВР МБОУ «Пушкинская СШ»
_____________ Завора А.В. « ____ »____________ 2016 г.
| УТВЕРЖДАЮ Директор МБОУ «Пушкинская СШ» _________Глущенко В.Д. Приказ № ________ от «___» ________2016 г. |
РАБОЧАЯ ПРОГРАММА
ПО УЧЕБНОМУ ПРЕДМЕТУ «АЛГЕБРА» (базовый уровень)
| (наименование учебного предмета/курса) 9-Б |
| (классы) |
Программу составила учитель __Мамбетова Венера Хайдаровна, _I-категории
(Ф.И.О., квалификационная категория учителя, составившего рабочую учебную программу)
с. Пушкино, 2016 г.
Пояснительная записка
Данная рабочая программа разработана в соответствии с основными положениями Федерального государственного образовательного стандарта и требованиями Примерной образовательной программы основного общего образования, с учетом основных идей и положений Программы развития и формирования универсальных учебных действий и ориентирована на использование учебно-методического комплекта:
Программы общеобразовательных учреждений. Алгебра. 7-9 классы / Ю.Н.Макарычев, Н.Г.Миндюк; составительН.Г.Миндюк – М.: Просвещение, 2014;
Алгебра: учебник для 9 класса общеобразовательных учреждений / [Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова]; под редакцией С.А.Теляковского – М.: Просвещение, 2014
Рабочая тетрадь. Авторы Ю.Н.Макарычев, Н.Г.Миндюк, И. С.Шлыкова.
Алгебра. 9 класс. Подготовка к государственной итоговой аттестации – 2010: учебно-методическое пособие / Ф.Ф.Лысенко – Ростов-на-Дону: Легион-М, 2009.
Поурочное планирование по алгебре: к учебнику Ю.Н.Макарычева, Н.Г.Миндюк, К.И.Нешкова, С.Б.Суворовой «Алгебра. 9 класс» / Т.М.Ерина – М.: Экзамен, 2008.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса. Содержание программы направлено на освоение учащимися знаний, умений и навыков на базовом уровне, что соответствует Образовательной программе школы. Она включает все темы, предусмотренные федеральным компонентом государственного образовательного стандарта основного общего образования по математике.
Место предмета в базисном учебном плане.
Согласно действующему учебному плану рабочая программа предусматривает обучение в объеме 102 часа из них 3ч. резерв (3 часа в неделю), в том числе для проведения
- Тематических контрольных работ - 7;
- Итоговых контрольных работ - 2
- итоговое повторение 21 ч.
В ходе освоения содержания курса учащиеся получают возможность:
развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
В ходе изучения алгебры в 9 классе учащиеся должны овладевать умениями общеучебного характера, разнообразными способами деятельности, приобретать опыт:
- планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
- решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
- исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
- ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
- проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
- поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Требования к уровню подготовки учащихся
В результате изучения математики ученик должен знать/понимать:
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов.
Должны уметь:
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики.
Должны владеть компетенциями: познавательной, коммуникативной, информационной и рефлексивной.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
Учащиеся должны достичь результатов обучения, представленных в Требованиях к уровню подготовки выпускников основной школы, достижение которых является обязательным условием положительной аттестации ученика за курс основной школы. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни». При этом последние два компонента представлены отдельно по каждому из разделов содержания.
Учащиеся должны достичь результатов обучения, представленных в Требованиях к уровню подготовки выпускников основной школы
Содержание программы учебного предмета
Квадратичная функция – 21ч
Функция. Возрастание и убывание функции. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Решение задач путем выделения квадрата двучлена из квадратного трехчлена. Функция y=ax2 + bx + с, её свойства, график. Простейшие преобразования графиков функций. Решение неравенств второй степени с одной переменной. [Решение рациональных неравенств методом интервалов.]
Цель – выработать умение строить график квадратичной функции и применять графические представления для решения неравенств второй степени с одной переменной.
Знать основные свойства функций, уметь находить промежутки знакопостоянства, возрастания, убывания функций
Уметь находить область определения и область значений функции, читать график функции
Уметь решать квадратные уравнения, определять знаки корней
Уметь выполнять разложение квадратного трехчлена на множители
Уметь строить график функции у=ах2 , выполнять простейшие преобразования графиков функций
Уметь строить график квадратичной функции, выполнять простейшие преобразования графиков функций
Уметь строить график квадратичной функции» находить по графику нули функции, промежутки, где функция принимает положительные и отрицательные значения.
Уметь построить график функции y=ax2 и применять её свойства. Уметь построить график функции y=ax2 + bx + с и применять её свойства
Уметь находить токи пересечения графика Квадратичной функции с осями координат. Уметь разложить квадратный трёхчлен на множители.
Уметь решать квадратное уравнение.
Уметь решать квадратное неравенство алгебраическим способом. Уметь решать квадратное неравенство с помощью графика квадратичной функции
Уметь решать квадратное неравенство методом интервалов. Уметь находить множество значений квадратичной функции.
Уметь решать неравенство ах2 +вх+с.≥0 на основе свойств квадратичной функции
Уравнения и неравенства с одной переменной -14ч
Целое уравнение и его корни. Решение уравнений третьей и четвертой степени с одним неизвестным с помощью разложения на множители и введения вспомогательной переменной.
Уравнение с двумя переменными и его график. Уравнение окружности. Решение систем, содержащих одно уравнение первой, а другое второй степени. Решение задач методом составления систем. Решение систем двух уравнений второй степени с двумя переменными.
Цель – выработать умение решать простейшие системы, содержащие уравнения второй степени с двумя переменными, и решать текстовые задачи с помощью составления таких систем.
Знать методы решения уравнений:
а) разложение на множители;
б) введение новой переменной;
в)графический способ.
Уметь решать целые уравнения методом введения новой переменной
Уметь решать системы 2 уравнений с 2 переменными графическим способом
Уметь решать уравнения с 2 переменными способом подстановки и сложения
Уметь решать задачи «на работу», «на движение» и другие составлением систем уравнений.
Уравнения и неравенства с двумя переменными -16ч
Четная и нечетная функции. Функция y=xn, Определение корня n-й степени.
Цель – ввести понятие корня n-й степени.
Знать определение и свойства четной и нечетной функций
Уметь строить график функции у=хn , знать свойства степенной функции с натуральным показателем, уметь решать уравнения хn=а при: а) четных и б)нечетных значениях n
Знать определение корня n- й степени, при каких значениях а имеет смысл выражение ![]()
Уметь выполнять простейшие преобразования и вычисления выражений, содержащих корни, применяя изученные свойства арифметического корня n-й степени
Знать, что степень с основанием, равным 0 определяется только для положительного дробного показателя и знать, что степени с дробным показателем не зависят от способа записи r в виде дроби
Знать свойства степеней с рациональным показателем, уметь выполнять простейшие преобразования выражений, содержащих степени с дробным показателем
Уметь выполнять преобразования выражений, содержащих степени с дробным показателем
Прогрессии – 14ч
Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы n первых членов прогрессии.
Цель – дать понятие об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.
Добиться понимания терминов «член последовательности», «номер члена последовательности», «формула n –го члена арифметической прогрессии»
Знать формулу n –го члена арифметической прогрессии, свойства членов арифметической прогрессии, способы задания арифметической прогрессии
Уметь применять формулу суммы n –первых членов арифметической прогрессии при решении задач
Знать, какая последовательность является геометрической, уметь выявлять, является ли последовательность геометрической, если да, то находить q
Уметь вычислять любой член геометрической прогрессии по формуле, знать свойства членов геометрической прогрессии
Уметь применять формулу при решении стандартных задач
Уметь применять формулу S=![]() при решении практических задач
при решении практических задач
Уметь находить разность арифметической прогрессии
Уметь находить сумму n первых членов арифметической прогрессии. Уметь находить
любой член геометрической прогрессии. Уметь
находить сумму n первых членов геометрической
прогрессии. Уметь решать задачи.
Элементы комбинаторики и теории вероятностей – 13ч
Комбинаторные задачи. Перестановки, размещения, сочетания. Перестановки. Размещения. Сочетания Вероятность случайного события
Знать формулы числа перестановок, размещений, сочетаний и уметь пользоваться ими.
Уметь пользоваться формулой комбинаторики при вычислении вероятностей
Повторение – 21 ч
Закрепление знаний, умений и навыков.
В целях качественной подготовки к ГИА повторение всего курса алгебры проводится в течении года плюс итоговое повторение в конце учебного года.
Почасовое планирование учебного материала в 9 классе.
(3 часа в неделю, всего – 102 часа из них 3ч. резерв)
| Раздел | Кол-во часов по программе | Кол-во контрольных работ |
| 1.Повторение за курс 8 кл. | 3 |
|
| 2. Квадратичная функция Ф-я, св-ва, графики, преобразование граф. Квадратные неравенства. Системы уравнений 2-ой степени. Степенная функция. Корень n-ой степени
| 21
| 2 |
| 3. Уравнения и неравенства с одной переменной. | 14 | 1 |
| 4. Уравнения и неравенства с двумя переменными | 16 | 1 |
| 5. Арифметическая и геометрическая прогрессии | 14 | 2 |
| 6. Элементы комбинаторики и теории вероятностей. | 13
| 1 |
| 7. Итоговое повторение. Подготовка к ГИА | 21 | 2 |
| Итого | 102 | 9 |
Календарно-тематическое планирование
Алгебра 9-Б класс
Всего: 102ч. из них 3ч. резерв в неделю 3 часа.
Учебник Алгебра: учебник для 9 класса общеобразовательных организаций / [Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворова]; под редакцией С.А.Теляковского – М.: Просвещение, 2014
|
№ ур. | Содержание материала |
Кол. часов | Дата |
Повторение | |
| По плану | По факту | ||||
| 1 | Повторение. Действия над рациональными дробями. Преобразование выражений, содержащие корни. | 1 |
|
|
|
| 2 | Повторение. Решение квадратных уравнений, дробно-рациональных уравнений. | 1 |
|
|
|
| 3 | Входная контрольная работа | 1 |
|
|
|
|
| Глава I Квадратичная функция | 21 |
|
|
|
| 4 | Функция. Область определения и область значений функции. | 1 |
|
| Формулы площадей и периметров. |
| 5 | Свойства функций | 1 |
|
|
|
| 6 | Свойства функций | 1 |
|
| Числовые неравенства. |
| 7 | Функция. Свойства функций | 1 |
|
|
|
| 8 | Квадратный трёхчлен и его корни | 1 |
|
| Обратная пропорциональность. |
| 9 | Разложение квадратного трёхчлена на множители | 1 |
|
|
|
| 10 | Разложение квадратного трёхчлена на множители | 1 |
|
| Свойства квадратичной функции. |
| 11 | Контрольная работа.№1
| 1 |
|
| Линейные неравенства с одной переменной. |
| 12 | Функция у=ах2, её график и свойства | 1 |
|
|
|
| 13 | Функция у=ах2, её график и свойства | 1 |
|
| Квадратичная функция. |
| 14 | Графики функций у=ах2+п, у=а(х-т)2 | 1 |
|
|
|
| 15 | Графики функций у=ах2+п, у=а(х-т)2 | 1 |
|
| Умножение и деление дробей. |
| 16 | Построение графика квадратичной функции | 1 |
|
|
|
| 17 | Построение графика квадратичной функции | 1 |
|
| Решение линейных уравнений. |
| 18 | Построение графика квадратичной функции | 1 |
|
|
|
| 19 | Построение графика квадратичной функции /Квадратичная функция/ | 1 |
|
| Основные свойства числовых неравенств. |
| 20 | Функция у = хп | 1 |
|
| Алгоритм решения уравнений. |
| 21 | Корень n-ой степени | 1 |
|
|
|
| 22 | Степень с рациональным показателем /Степень с рациональным показателем, корень n-ой степени/ | 1 |
|
| Неполные квадратные уравнения. |
| 23 | Степень с рациональным показателем /Степень с рациональным показателем, корень n-ой степени/ | 1 |
|
| Основные свойства числовых неравенств. |
| 24 | Контрольная работа №2. Квадратичная функция | 1 |
|
|
|
|
| Глава II Уравнения и неравенства с одной переменной | 14 |
|
|
|
| 25 | Целое уравнение и его корни | 1 |
|
| Основные свойства числовых неравенств. |
| 26 | Целое уравнение и его корни | 1 |
|
|
|
| 27 | Целое уравнение и его корни | 1 |
|
| Решение задач с помощью уравнений. |
| 28 | Дробные рациональные уравнения | 1 |
|
|
|
| 29 | Дробные рациональные уравнения | 1 |
|
| Решение задач на процентные расчеты. |
| 30-31 | Дробные рациональные уравнения Контрольная работа.Пробный экзамен | 2 |
|
|
|
| 32 | Решение неравенств второй степени с одной переменной | 1 |
|
| Формула корней квадратного уравнения. |
| 33-34 | Решение неравенств второй степени с одной переменной /Решение неравенств/ | 2 |
|
|
|
| 35 | Решение неравенств методом интервалов | 1 |
|
| Основные свойства числовых неравенств. |
| 36 | Решение неравенств методом интервалов | 1 |
|
|
|
| 37 | Решение неравенств методом интервалов | 1 |
|
| Определение функции. |
| 38 | Контрольная работа №3. Уравнения и неравенства с одной переменной | 1 |
|
|
|
|
| Глава III Уравнения и неравенства с двумя переменными | 16 |
|
|
|
| 39 | Уравнение с двумя переменными и его график | 1 |
|
| Свойства функции. |
| 40 | Уравнение с двумя переменными и его график | 1 |
|
| График линейной функции. |
| 41 | Графический способ решения систем уравнений | 1 |
|
|
|
| 42 | Графический способ решения систем уравнений | 1 |
|
| Умножение и деление дробей. |
| 43 | Решение систем уравнений второй степени | 1 |
|
|
|
| 44 | Решение систем уравнений второй степени | 1 |
|
|
|
| 45 | Решение систем уравнений второй степени | 1 |
|
| Решение линейных уравнений. |
| 46 | Решение задач с помощью систем уравнений второй степени | 1 |
|
|
|
| 47 | Решение задач с помощью систем уравнений второй степени | 1 |
|
| Функции и их графики. |
| 48 | Решение задач с помощью систем уравнений второй степени | 1 |
|
|
|
| 49 | Решение задач с помощью систем уравнений второй степени /Решение систем уравнений второй степени и задач с помощью систем уравнений/ | 1 |
|
| Решение задач на проценты. |
| 50 | Неравенства с двумя переменными | 1 |
|
|
|
| 51 | Неравенства с двумя переменными | 1 |
|
| Методы решения систем. |
| 52 | Системы неравенств с двумя переменными | 1 |
|
|
|
| 53 | Системы неравенств с двумя переменными | 1 |
|
| Решение линейных неравенств. |
| 54 | Контрольная работа №4. Уравнения и неравенства с двумя переменными | 1 |
|
|
|
|
| Глава IY Арифметическая и геометрическая прогрессии |
14 |
|
|
|
| 55 | Последовательности. Определение арифметической прогрессии | 1 |
|
|
|
| 56 | Определение арифметической прогрессии. Формула n-ого члена арифметической прогрессии | 1 |
|
| Разложения многочлена на множители. |
| 57 | Формула n-ого члена арифметической прогрессии | 1 |
|
| Формула n-го члена ариф-метической прогрессии. |
| 58 | Формула суммы n первых членов арифметической прогрессии | 1 |
|
|
|
| 59 | Формула суммы n первых членов арифметической прогрессии | 1 |
|
| Сокращение дробей. |
| 60 | Формула суммы n первых членов арифметической прогрессии | 1 |
|
| Свойства арифметического квадратного корня. |
| 61 | Контрольная работа №5. Арифметическая прогрессия | 1 |
|
|
|
| 62 | Определение геометрической прогрессии. Формула n-ого члена геометрической прогрессии | 1 |
|
| Свойства степеней. |
| 63-64 | Формула n-ого члена геометрической прогрессии | 2 |
|
| Решение систем неравенств. |
| 65 | Формула суммы n первых членов геометрической прогрессии | 1 |
|
| Квадратичная функция, свойства, график. |
| 66 | Формула суммы n первых членов геометрической прогрессии /Прогрессии/ | 1 |
|
|
|
| 67 | Формула суммы n первых членов геометрической прогрессии | 1 |
|
| Прогрессии. |
| 68 | Контрольная работа №6. Геометрическая прогрессия | 1 |
|
|
|
|
| Глава Y Элементы комбинаторики и теории вероятностей | 13 |
|
|
|
| 69-70 | Примеры комбинаторных задач | 2 |
|
| Пропорции. |
| 71 | Перестановки | 1 |
|
| Среднее арифметическое чисел. |
| 72 | Размещения | 1 |
|
|
|
| 73 | Сочетания | 1 |
|
| Область определения функции. |
| 74 | Перестановки, размещения сочетания | 1 |
|
|
|
| 75 | Перестановки, размещения сочетания | 1 |
|
| Диаграммы. |
| 76 | Относительная частота случайного события | 1 |
|
|
|
| 77 | Относительная частота случайного события /Комбинаторные задачи/ | 1 |
|
| Решение задач на проценты. |
| 78 | Решение задач | 1 |
|
|
|
| 79-80 | Вероятность равновозможных событий | 2 |
|
| Линейная функция и ее свойства. |
| 81 | Контрольная работа №7. Элементы комбинаторики и теории вероятностей | 1 |
|
|
|
|
| Итоговое повторение. Подготовка к ГИА | 21 |
|
|
|
| 82-83 | Квадратичная функция | 2 |
|
|
|
| 84-86 | Уравнения и неравенства с одной переменной | 3 |
|
|
|
| 87-88 | Уравнения и неравенства с двумя переменной | 2 |
|
|
|
| 89-90 | Арифметическая и геометрическая прогрессии | 2 |
|
|
|
| 91 | Контрольная работа№8. | 1 |
|
|
|
| 92-93 | Элементы комбинаторики и теории вероятностей | 2 |
|
|
|
| 94-96 | Системы уравнений. Решение текстовых задач | 3 |
|
|
|
| 97-99 | Системы неравенств | 3 |
|
|
|
| 100 | Итоговая контрольная работа№9 | 1 |
|
|
|
| 101 | Обобщение и систематизация материала | 1 |
|
|
|
| 102 | Итоговый урок | 1 |
|
|
|
Просмотр содержимого документа
«АЛГЕБРА 8 кл»
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ПУШКИНСКАЯ СРЕДНЯЯ ШКОЛА»
СОВЕТСКОГО РАЙОНА РЕСПУБЛИКИ КРЫМ
| РАССМОТРЕНО на МО учителей естественно -математического цикла Протокол № от « ___ »_____________2016 г. Руководитель МО ____________ Смеянова Т.В. | СОГЛАСОВАНО Заместитель директора по УВР МБОУ «Пушкинская СШ»
_____________ Завора А.В. « ____ »____________ 2016 г.
| УТВЕРЖДАЮ Директор МБОУ «Пушкинская СШ» _________Глущенко В.Д. Приказ № ________ от «___» ________2016 г. |
РАБОЧАЯ ПРОГРАММА
ПО УЧЕБНОМУ ПРЕДМЕТУ «АЛГЕБРА» (базовый уровень)
| (наименование учебного предмета/курса) 8 |
| (классы) |
Программу составила учитель __Мамбетова Венера Хайдаровна, _I-категории
(Ф.И.О., квалификационная категория учителя, составившего рабочую учебную программу)
с. Пушкино, 2016 г.
Пояснительная записка.
Данная рабочая программа разработана в соответствии с основными положениями Федерального государственного образовательного стандарта и требованиями Примерной образовательной программы основного общего образования, с учетом основных идей и положений Программы развития и формирования универсальных учебных действий и ориентирована на использование учебно-методического комплекта:
Программы общеобразовательных учреждений. Алгебра. 7-9 классы / Ю.Н.Макарычев, Н.Г.Миндюк; составительН.Г.Миндюк – М.: Просвещение, 2014;
Государственный стандарт основного общего образования по математике.
Программа соответствует учебнику «Алгебра. 8 класс» / Ю.Н. Макарычев, Н.Г. Миндюк и др.; под ред. С.А. Теляковского. М.: Просвещение, 2014.
Примерная программа конкретизирует содержание предметных тем образовательного стандарта и даёт примерное распределение учебных часов по разделам курса.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает распределение учебных часов по разделам курса. Содержание программы направлено на освоение учащимися знаний, умений и навыков на базовом уровне, что соответствует Образовательной программе школы. Она включает все темы, предусмотренные федеральным компонентом государственного образовательного стандарта основного общего образования по математике.
Место предмета в базисном учебном плане.
Согласно действующему учебному плану рабочая программа предусматривает обучение в объеме 105 часов.из них3ч. резерв. (3 часа в неделю)
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ
ИЗУЧЕНИЯ КУРСА АЛГЕБРЫ В 8 КЛАССЕ.
В результате изучения алгебры ученик должен
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
уметь
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним;
решать линейные неравенства с одной переменной и их системы;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
Для оценки учебных достижений обучающихся используется:
Диагностическая контрольная работа–1.
Тематические контрольные работы – 9.
Итоговая контрольная работа – 1.
В связи с необходимостью провести обобщающее повторение материала 7 класса целесообразным является введение раздела «Повторение» (3 часа) в начале учебного года.
СОДЕРЖАНИЕ КУРСА АЛГЕБРЫ
(3 часа в неделю, всего 105 часов из них 3ч. резерв)
1. Рациональные дроби (23 часа)
Рациональная дробь.Основное свойство дроби, сокращение дробей. Тождественные преобразования рациональных выражений.
Функция  и ее график.
и ее график.
Основная цель — выработать умение выполнять тождественные преобразования рациональных выражений.
Так как действия с рациональными дробями существенным образом опираются на действия с многочленами, то в начале темы необходимо повторить с учащимися преобразования целых выражений.
Главное место в данной теме занимают алгоритмы действий с дробями. Учащиеся должны понимать, что сумму, разность, произведение и частное дробей всегда можно представить в виде дроби. Приобретаемые в данной теме умения выполнять сложение, вычитание, умножение и деление дробей являются опорными в преобразованиях дробных
выражений. Поэтому им следует уделить особое внимание. Нецелесообразно переходить к комбинированным заданиям на все действия с дробями прежде, чем будут усвоены основные алгоритмы. Задания на все действия с дробями не должны быть излишне громоздкими и трудоемкими.
При нахождении значений дробей даются задания на вычисления с помощью калькулятора. В данной теме расширяются сведения о статистических характеристиках. Вводится понятие среднего гармонического ряда положительных чисел.
Изучение темы завершается рассмотрением свойств графика функции

2. Квадратные корни (19 часов)
Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция  , ее свойства и график.
, ее свойства и график.
Основная цель — систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие о числе; выработать умение выполнять преобразования выражений, содержащих квадратные корни.
В данной теме учащиеся получают начальное представление о понятии действительного числа. С этой целью обобщаются известные учащимся сведения о рациональных числах. Для введения понятия иррационального числа используется интуитивное представление о том, что каждый отрезок имеет длину и потому каждой точке координатной прямой соответствует некоторое число. Показывается, что существуют точки, не имеющие рациональных абсцисс.
При введении понятия корня полезно ознакомить учащихся с нахождением корней с помощью калькулятора.
Основное внимание уделяется понятию арифметического квадратного корня и свойствам арифметических квадратных корней. Доказываются теоремы о корне из произведения и дроби, а также тождество  , которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида
, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида  ,
, 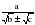 . Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
. Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
Продолжается работа по развитию функциональных представлений учащихся. Рассматриваются функция  её свойства и график. При изучении функции
её свойства и график. При изучении функции  показывается ее взаимосвязь с функцией
показывается ее взаимосвязь с функцией  , где
, где 
3. Квадратные уравнения (20 час)
Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.
Основная цель — выработать умения решать квадратные уравнения и простейшие рациональные уравнения и применять их к решению задач.
В начале темы приводятся примеры решения неполных квадратных уравнений. Этот материал систематизируется. Рассматриваются алгоритмы решения неполных квадратных уравнений различного вида.
Основное внимание следует уделить решению уравнений вида  , где
, где  , с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.
, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.
Учащиеся овладевают способом решения дробных рациональных уравнений, который состоит в том, что решение таких уравнений сводится к решению соответствующих целых уравнений с последующим исключением посторонних корней.
Изучение данной темы позволяет существенно расширить аппарат уравнений, используемых для решения текстовых задач.
4. Неравенства (20 часов)
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.
Основная цель — ознакомить учащихся с применением неравенств для оценки значений выражений, выработать умение решать линейные неравенства с одной переменной и их системы.
Свойства числовых неравенств составляют ту базу, на которой основано решение линейных неравенств с одной переменной. Теоремы о почленном сложении и умножении неравенств находят применение при выполнении простейших упражнений на оценку выражений по методу границ. Вводятся понятия абсолютной погрешности и точности приближения, относительной погрешности.
Умения проводить дедуктивные рассуждения получают развитие как при доказательствах указанных теорем, так и при выполнении упражнений на доказательства неравенств.
В связи с решением линейных неравенств с одной переменной дается понятие о числовых промежутках, вводятся соответствующие названия и обозначения. Рассмотрению систем неравенств с одной переменной предшествует ознакомление учащихся с понятиями пересечения и объединения множеств.
При решении неравенств используются свойства равносильных неравенств, которые разъясняются на конкретных примерах. Особое внимание следует уделить отработке умения решать простейшие неравенства вида ax b, ах b, остановившись специально на случае, когда а 0.
В этой теме рассматривается также решение систем двух линейных неравенств с одной переменной, в частности таких, которые записаны в виде двойных неравенств.
5. Степень с целым показателем. Элементы статистики (10 часов)
Степень с целым показателем и ее свойства. Стандартный вид числа. Начальные сведения об организации статистических исследований.
Основная цель — выработать умение применять свойства степени с целым показателем в вычислениях и преобразованиях, сформировать начальные представления о сборе и группировке статистических данных, их наглядной интерпретации.
В этой теме формулируются свойства степени с целым показателем. Метод доказательства этих свойств показывается на примере умножения степеней с одинаковыми основаниями. Дается понятие о записи числа в стандартном виде. Приводятся примеры использования такой записи в физике, технике и других областях знаний.
Учащиеся получают начальные представления об организации статистических исследований. Они знакомятся с понятиями генеральной и выборочной совокупности. Приводятся примеры представления статистических данных в виде таблиц частот и относительных частот. Учащимся предлагаются задания на нахождение по таблице частот таких статистических характеристик, как среднее арифметическое, мода, размах. Рассматривается вопрос о наглядной интерпретации статистической информации. Известные учащимся способы наглядного представления статистических данных с помощью столбчатых и круговых диаграмм расширяются за счет введения таких понятий, как полигон и гистограмма.
6. Повторение (7 часов).
В связи с необходимостью провести обобщающее повторение материала 7 класса целесообразным является введение раздела «Повторение» (3 часа) в начале учебного года.
тематическое ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА.
3 УРОКА В НЕДЕЛЮ (105 УРОКОВ из них3ч. резерв)
| № | Содержание учебного материала |
|
|
| Кол-во часов | Кол-во контр-ных работ. | ||
| 1. | Повторение курса 7 класса | 3 |
|
| 2. | Рациональные дроби и их свойства | 23 | 2 |
| 3. | Квадратные корни | 19 | 2 |
| 4. | Квадратные уравнения | 20 | 2 |
| 5. | Неравенства | 20 | 2 |
| 6. | Степень с целым показателем. Элементы статистики | 10 | 1 |
| 7. | Итоговое повторение курса алгебры 8 класса. | 7 | 1 |
| 8. | Резерв | 3 |
|
|
| Итого | 105 | 10 |
Календарно-тематическое планирование
по алгебре, 8 класс.
Всего: 105ч. из них 3ч. резерв в неделю 3 часа.
Учебник: Макарычев, Ю. Н. Алгебра: учебник для 8 класса общеобразовательных организаций / Ю. Н. Макарычев, К. И. Нешков, Н. Г. Миндюк, С. Б. Суворова; под ред. С. А. Теляковского. - М.: Просвещение, 2014 г.
| № | Содержание учебного материала | Кол. часов | Дата | Повторение | ||||||
| По плану | По факту | |||||||||
|
| Повторение | 3 |
|
|
| |||||
| 1 | Формулы сокращенного умножения Способы разложения многочлена на множители | 1 |
|
|
| |||||
| 2 | Системы линейных уравнений. Линейная функция | 1 |
|
|
| |||||
| 3 | Входной контроль | 1 |
|
|
| |||||
|
| Рациональные дроби и их свойства | 23 |
|
|
| |||||
| 4 | Рациональные выражения, п. 1 | 1 |
|
| Линейные уравнения | |||||
| 5 | Рациональные дроби, п. 1 | 1 |
|
| Основное свойство дроби | |||||
| 6 | Основное свойство дроби, п. 2 | 1 |
|
| Разложение на множители | |||||
| 7-8 | Сокращение дробей, п. 2 | 2 |
|
| Формулы сокращенного умножения (ФСУ) | |||||
| 9 | Сложение дробей с одинаковыми знаменателями, п.3 | 1 |
|
|
Действия с обыкновенными дробями | |||||
| 10 | Вычитание дробей с одинаковыми знаменателями, п.3 | 1 |
|
| ||||||
| 11 | Сложение дробей с разными знаменателями, п. 4 | 1 |
|
| ||||||
| 12-13 | Вычитание дробей с разными знаменателями, п. 4 | 2 |
|
| ||||||
| 14 | Урок обобщения и систематизации знаний | 1 |
|
| П. 1 – 4 | |||||
| 15 | Контрольная работа №1 | 1 |
|
|
| |||||
| 16 | Умножение дробей, п. 5 | 1 |
|
| Степень с натуральным показателем | |||||
| 17 | Возведение дроби в степень, п. 5 | 1 |
|
| Свойства степеней. ФСУ, разложение на множители | |||||
| 18 | Деление дробей, п. 6 | 1 |
|
| ||||||
| 19 | Деление дробей, п. 6 | 1 |
|
| ||||||
| 20 | Преобразование рациональных выражений, п. 7 | 1 |
|
| Составление и работа с математической моделью | |||||
| 21 | Преобразование рациональных выражений, п. 7 | 1 |
|
| ||||||
| 22 | Преобразование рациональных выражений, п. 7 | 1 |
|
| Допустимые значения переменных | |||||
| 23 | Функция | 1 |
|
| Линейная функция | |||||
| 24 | Функция | 1 |
|
| Решение уравнений графически | |||||
| 25 | Урок обобщения и систематизации знаний | 1 |
|
| П. 5 – 8 | |||||
| 26 | Контрольная работа №2 | 1 |
|
|
| |||||
|
| Глава II. Квадратные корни | 19 |
|
|
| |||||
| 27 | Рациональные числа, п. 10 | 1 |
|
| Натуральные, целые числа | |||||
| 28 | Иррациональные числа, п. 11 | 1 |
|
| Рациональные числа | |||||
| 29 | Квадратные корни. Арифметический квадратный корень, п. 12 | 1 |
|
| Степень с натуральным показателем | |||||
| 30 | Уравнение | 1 |
|
| Уравнения. Корень уравнения | |||||
| 31 | Уравнение | 1 |
|
| ||||||
| 32 | Нахождение приближенных значений квадратного корня, п.14 | 1 |
|
| Действия с алгебраическими дробями | |||||
| 33 | Функция | 1 |
|
| Линейная функция и её график | |||||
| 34 | Функция | 1 |
|
| ||||||
| 35 | Квадратный корень из произведения и дроби, п.16 | 1 |
|
| Некоторые символы математического языка | |||||
| 36 | Квадратный корень из произведения и дроби, п.16 | 1 |
|
| ||||||
| 37 | Квадратный корень из степени, п.17 | 1 |
|
| Преобразование выражений | |||||
| 38 | Урок обобщения и систематизации знаний | 1 |
|
| П. 10 – 17 | |||||
| 39 | Контрольная работа №3 | 1 |
|
|
| |||||
| 40 | Вынесение множителя из-под знака корня, п. 18 | 1 |
|
| Составление и работа с математической моделью | |||||
| 41 | Внесение множителя под знак корня, п.18 | 1 |
|
| ||||||
| 42 | Преобразование выражений, содержащих квадратные корни, п.19 | 1 |
|
| Формулы сокращенного умножения, разложение на множители | |||||
| 43 | Преобразование выражений, содержащих квадратные корни, п.19 | 1 |
|
| ||||||
| 44 | Урок обобщения и систематизации знаний | 1 |
|
| П. 18 – 19 | |||||
| 45 | Контрольная работа №4 | 1 |
|
|
| |||||
|
| Глава III. Квадратные уравнения | 20 |
|
|
| |||||
| 46 | Определение квадратного уравнения, п. 21 | 1 |
|
| Уравнения и его корни | |||||
| 47 | Неполные квадратные уравнения, п. 21 | 1 |
|
| Приемы устного счета | |||||
| 48 | Решение квадратных уравнений по формуле D, п.22 | 1 |
|
| Преобразование выра-жений,содержащие корни | |||||
| 49 | Решение квадратных уравнений по формуле D1, п. 22 | 1 |
|
| Свойства степеней. задачи на проценты. | |||||
| 50 | Решение квадратных уравнений, п. 22 | 1 |
|
| Формулы сокращенного умножения. | |||||
| 51 | Решение квадратных уравнений, п. 22 | 1 |
|
| Решение квадратных уравнений на множители. | |||||
| 52 | Решение задач с помощью квадратных уравнений, п.23 | 1 |
|
| Формула корней квадратного уравнения. | |||||
| 53 | Решение задач с помощью квадратных уравнений, п. 23 | 1 |
|
| Квадрат двучлена. | |||||
| 54 | Теорема Виета, п. 24 | 1 |
|
|
| |||||
| 55 | Теорема Виета, п. 24 | 1 |
|
| П. 21 – 24 | |||||
| 56 | Контрольная работа №5 | 1 |
|
|
| |||||
| 57 | Решение дробных рациональных уравнений, п. 25 | 1 |
|
| Рациональные дроби. | |||||
| 58 | Решение дробных рациональных уравнений, п. 25 | 1 |
|
|
| |||||
| 59 | Решение дробных рациональных уравнений, п. 25 | 1 |
|
| Свойства степеней. | |||||
| 60 | Решение дробных рациональных уравнений, п. 25 | 1 |
|
|
| |||||
| 61 | Решение задач с помощью рациональных уравнений, п. 26 | 1 |
|
| Проценты. | |||||
| 62 | Решение задач с помощью рациональных уравнений, п. 26 | 1 |
|
| Формула пути. | |||||
| 63 | Решение задач с помощью рациональных уравнений, п. 26 | 1 |
|
|
| |||||
| 64 | Урок обобщения и систематизации знаний | 1 |
|
| П. 25 – 26 | |||||
| 65 | Контрольная работа №6 | 1 |
|
|
| |||||
|
| Глава IV. Неравенства | 20 |
|
|
| |||||
| 66 | Числовые неравенства, п. 28 | 1 |
|
| Решение задач на движение. | |||||
| 67 | Свойства числовых неравенств, п. 29 | 1 |
|
| Действия над рациональными числами. | |||||
| 68 | Свойства числовых неравенств, п. 29 | 1 |
|
| Решение уравнений | |||||
| 69 | Сложение числовых неравенств, п. 30 | 1 |
|
| Формулы площадей и периметров. | |||||
| 70 | Умножение числовых неравенств, п. 30 | 1 |
|
| Числовые неравенства. | |||||
| 71 | Погрешность и точность приближения, п. 31 | 1 |
|
|
| |||||
| 72 | Погрешность и точность приближения, п. 31 | 1 |
|
| П. 28 – 31 | |||||
| 73 | Урок обобщения и систематизации знаний | 1 |
|
|
| |||||
| 74 | Контрольная работа №7 | 1 |
|
|
| |||||
| 75 | Пересечение множеств, п. 32 | 1 |
|
| Алгоритм решения уравнений. | |||||
| 76 | Объединение множеств, п. 32 | 1 |
|
| Неполные квадратные уравнения. | |||||
| 77 | Числовые промежутки, п. 33 | 1 |
|
| Основные свойства числовых неравенств. | |||||
| 78 | Решение неравенств с одной переменной, п. 34 | 1 |
|
|
| |||||
| 79 | Решение неравенств с одной переменной, п. 34 | 1 |
|
| Решение задач с помощью уравнений. | |||||
| 80 | Решение неравенств с одной переменной, п. 34 | 1 |
|
|
| |||||
| 81 | Решение систем неравенств с одной переменной, п. 35 | 1 |
|
| Проценты. | |||||
| 82 | Решение систем неравенств с одной переменной. | 1 |
|
|
| |||||
| 83 | Решение систем неравенств с одной переменной, п. 35 | 1 |
|
| Решение задач на процентные расчеты. | |||||
| 84 | Урок обобщения и систематизации знаний | 1 |
|
| П. 32 – 35 | |||||
| 85 | Контрольная работа №8 | 1 |
|
|
| |||||
|
| Глава V. Степень с целым показателем. Элементы статистики | 10 |
|
|
| |||||
| 86 | Определение степени с целым отрицательным показателем, п. 37 | 1 |
|
| Свойства степеней. | |||||
| 87 | Степень с целым отрицательным показателем, п. 37 | 1 |
|
| Решение задач на движение. | |||||
| 88 | Свойства степени с целым показателем, п. 38 | 1 |
|
| Умножение одночленов. | |||||
| 89 | Свойства степени с целым показателем, п. 38 | 1 |
|
| Рациональные дроби. | |||||
| 90 | Стандартный вид числа, п. 39 | 1 |
|
| Свойства степеней. | |||||
| 91 | Сбор и группировка статистических данных, п. 40 | 1 |
|
| Линейная функция. | |||||
| 92 | Сбор и группировка статистических данных, п. 40 | 1 |
|
| Рациональные числа. | |||||
| 93 | Наглядное представление статистической информации, п. 41 | 1 |
|
| Решение уравнений. | |||||
| 94 | Урок обобщения и систематизации знаний | 1 |
|
| Функции и их графики. | |||||
| 95 | Контрольная работа №9 | 1 |
|
|
| |||||
|
| Повторение | 7 |
|
|
| |||||
| 96 | Повторение темы «Преобразование рациональных выражений». | 1 |
|
|
| |||||
| 97 | Повторение темы «Преобразование выражений, содержащих квадратные корни». | 1 |
|
|
| |||||
| 98 | Повторение темы «Решение квадратных уравнений». | 1 |
|
|
| |||||
| 99 | Повторение темы «Решение дробных рациональных уравнений». | 1 |
|
|
| |||||
| 100 | Повторение темы «Решение систем неравенств с одной переменной». | 1 |
|
|
| |||||
| 101 | Итоговая контрольная работа. | 1 |
|
|
| |||||
| 102 | Обобщение материала, выученного за год | 1 |
|
|
| |||||
| 103-105 |
Резерв |
3 |
|
|
| |||||
Просмотр содержимого документа
«АЛГЕБРА 10кл.»
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ПУШКИНСКАЯ СРЕДНЯЯ ШКОЛА»
СОВЕТСКОГО РАЙОНА РЕСПУБЛИКИ КРЫМ
| РАССМОТРЕНО на МО учителей естественно - математического цикла Протокол №____ от « ___ »___________2016 г. Руководитель МО ____________ Смеянова Т.В. | СОГЛАСОВАНО Заместитель директора по УВР МБОУ «Пушкинская СШ» _____________ Завора А.В. от« ____ »__________2016 г.
| УТВЕРЖДАЮ Директор МБОУ «Пушкинская СШ» ______Глущенко В.Д. Приказ № ___ от «___»________2016 г. |
РАБОЧАЯ ПРОГРАММА
ПО УЧЕБНОМУ ПРЕДМЕТУ «АЛГЕБРА И НАЧАЛА АНАЛИЗА»
(базовый уровень)
| (наименование учебного предмета/курса) 10 |
| (классы)
|
Программу составила учитель __Мамбетова Венера Хайдаровна, _I-категории
(Ф.И.О., квалификационная категория учителя, составившего рабочую учебную программу)
с. Пушкино, 2016г.
Пояснительная записка
Рабочая программа учебного курса по алгебре для 10 класса разработана на основе нормативного обеспечения программы:
1. Федеральный закон от 29.12.2012 г. № 273-ФЗ «Об образовании в Российской Федерации» (редакция от 23.07.2013).
2. Об утверждении Федерального перечня учебников, рекомендованных к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования / Приказ Министерства образования и науки Российской Федерации от 31.03.2014 г. № 253
3. Об утверждении федерального базисного учебного плана и примерных учебных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования»/ Приказ Министерства образования и науки Российской Федерации от 09.03. 2004 года № 1312.
4.Об утверждении Федерального компонента государственного образовательного стандарта начального общего, основного общего и среднего (полного) общего образования / Приказ Министерства образования и науки Российской Федерации от 05.03.2004 г. № 1089.
5. О примерных программах по учебным предметам федерального базисного учебного плана / Приказ Министерства образования и науки Российской Федерации от 07.07.2005 г. № 03-126.
Рабочая программа составлена с учетом следующего учебно-методического комплекса:
программы для общеобразовательных учреждений. Алгебра и начала математического анализа. 10-11 классы./сост Т.А. Бурмистрова. – М.: Просвещение, 2010.
С. М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. «Алгебра и начала математического анализа. 10 класс. – М.: Просвещение, 2014.
«Алгебра и начала анализа 10» Дидактические материалы для 10 класса. Авт.М.К. Потапов, А.В. Шевкин М.: Просвещение, 2014. Уровень обучения – базовый.
Место предмета в учебном плане
Данная программа рассчитана на 105ч.из них 3ч. резерв. В учебном плане для изучения алгебры и начал анализа на базовом уровне отводится 3 часа в неделю.
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОСВОЕНИЯ УЧЕБНОГО ПРЕДМЕТА.
В результате изучения курса математики 10 класса обучающиеся должны:
Знать/понимать
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира.
Алгебра
Уметь
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
находить по графику функции наибольшие и наименьшие значения;
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.
Начала математического анализа
Уравнения и неравенства
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
составлять уравнения и неравенства по условию задачи;
использовать графический метод для приближенного решения уравнений и неравенств;
изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
построения и исследования простейших математических моделей.
Элементы теории вероятностей
уметь
вычислять в простейших случаях вероятности событий на основе подсчета числа исходов;
Общеучебные умения, навыки и способы деятельности
В ходе преподавания математики в 10 классе, работа над формированием у обучающихся перечисленных в программе знаний и умений следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА.
| Раздел | Количество часов в рабочей программе | Количество контрольных работ |
| Повторение за 9 класс | 3 |
|
| Действительные числа | 6 |
|
| Рациональные уравнения и неравенства | 14 | 1 |
| Корень степени n | 8 | 1 |
| Степень положительного числа | 8 | 1 |
| Логарифмы | 6 |
|
| Показательные и логарифмические уравнения и неравенства | 8 | 1 |
| Синус и косинус угла | 7 |
|
| Тангенс и котангенс угла | 4 | 1 |
| Формулы сложения | 10 |
|
| Тригонометрические функции числового аргумента | 7 | 1 |
| Тригонометрические уравнения и неравенства | 7 | 1 |
| Вероятность события | 4 |
|
| Повторение | 10 | 1 |
| Резерв | 3 |
|
| Итого | 105 | 8 |
Отличительная особенность рабочей программы
В тему 10 класса «Действительные числа 6 ч.» включены темы 11 класса «Перестановки, размещения, сочетания » одного урока, входящие в тему: «Элементы комбинаторики, теории вероятностей и математической статистики 12 ч.».
В перечень изучаемых тем 10 класса (14 часов) включены следующие темы 11 класса «Логарифмы» и «Решение показательных и логарифмических уравнений и неравенств».
Содержание учебного предмета «Алгебра и начала анализа»
| № п/п | Тема | Содержание | |
| 10 класс | |||
| 1 | Действительные числа | Понятие действительного числа. Множества чисел. Свойства действительных чисел. Перестановки. Размещения. Сочетания. | |
| 2 | Рациональные уравнения и неравенства | В этой главе приходится решение параметрических неравенств, доказательство неравенств, решение уравнений и неравенств, содержащих два и более модулей. В более усложненной форме дается построение графиков функций, формулы которых содержат два и более модулей. Доказываются равенства методом математической индукции.
| |
| 3 | Корень n-ой степени | Определение корня n-ой степени и его свойств. Вычисление корня натуральной степени из числа. Преобразование иррациональных выражений. Вычисление корня из комплексного числа. | |
| 4 | Степень с действительным показателем | Определение степени с рациональным показателем и ее свойств. Определение степени с действительными показателями и ее свойств. Преобразование степенных выражений, используя свойства степени. | |
| 5 | Тригонометрические функции | Тождественные преобразования тригонометрических выражений. Тригонометрические функции числового аргумента: синус, косинус и тангенс. Периодические функции. Свойства и графики тригонометрических функций. Цель: расширить и закрепить знания и умения, связанные с тождественными преобразованиями тригонометрических выражений; изучить свойства тригонометрических функций и познакомить учащихся с их графиками. Изучение темы начинается с вводного повторения, в ходе которого напоминаются основные формулы тригонометрии, известные из курса алгебры, и выводятся некоторые новые формулы. От учащихся не требуется точного запоминания всех формул. Предполагается возможность использования различных справочных материалов: учебника, таблиц, справочников. Особое внимание следует уделить работе с единичной окружностью. Она становится основой для определения синуса и косинуса числового аргумента и используется далее для вывода свойств тригонометрических функций и решения тригонометрических уравнений. Систематизируются сведения о функциях и графиках, вводятся новые понятия, связанные с исследованием функций (экстремумы, периодичность), и общая схема исследования функций. В соответствии с этой общей схемой проводится исследование функций синус, косинус, тангенс и строятся их графики. Материал учебника, касающийся тригонометрических неравенств и систем уравнений, не является обязательным. | |
| 6 | Тригонометрические уравнения | Простейшие тригонометрические уравнения. Решение тригонометрических уравнений. Цель: сформировать умение решать простейшие тригонометрические уравнения и познакомить с некоторыми приемами решения тригонометрических уравнений. Решение простейших тригонометрических уравнений основывается на изученных свойствах тригонометрических функций. При этом целесообразно широко использовать графические иллюстрации с помощью единичной окружности. Отдельного внимания заслуживают уравнения вида Отработка каких-либо специальных приемов решения более сложных тригонометрических уравнений не предусматривается. Достаточно рассмотреть отдельные примеры решения таких уравнений, подчеркивая общую идею решения: приведение уравнения к виду, содержащему лишь одну тригонометрическую функцию одного и того же аргумента, с последующей заменой. Материал, касающийся тригонометрических неравенств и систем уравнений, не является обязательным. Как и в предыдущей теме, предполагается возможность использования справочных материалов. | |
| 7 | Показательная и логарифмическая функции | Понятие о степени с иррациональным показателем. Решение иррациональных уравнений. Показательная функция, ее свойства и график. Тождественные преобразования показательных уравнений, неравенств и систем. Логарифм числа. Основные свойства логарифмов. Логарифмическая функция, ее свойства и график. Решение логарифмических уравнений и неравенств. Производная показательной функции. Число е и натуральный логарифм. Производная степенной функции. Цель: привести в систему и обобщить сведения о степенях; ознакомить с показательной, логарифмической и степенной функциями и их свойствами; научить решать несложные показательные, логарифмические и иррациональные уравнения, их системы. Следует учесть, что в курсе алгебры девятилетней школы вопросы, связанные со свойствами корней n-й степени и свойствами степеней с рациональным показателем, возможно, не рассматривались, изучение могло быть ограничено действиями со степенями с целым показателем и квадратными корнями. В зависимости от реальной подготовки класса эта тема изучается либо в виде повторения, либо как новый материал. Серьезное внимание следует уделить работе с основными логарифмическими и показательными тождествами, которые используются как при изложении теоретических вопросов, так и при решении задач. Исследование показательной, логарифмической и степенной функций проводится в соответствии с ранее введенной схемой. Проводится краткий обзор свойств этих функций в зависимости от значений параметров. Раскрывается роль показательной функции как математической модели, которая находит широкое применение при изучении различных процессов. Материал об обратной функции не является обязательным. | |
| 8 | Элементы теории вероятностей | Понятие вероятности события. Свойства вероятностей событий | |
Просмотр содержимого документа
«кал. план.алебра11кл.»
Алгебра и начала математического анализа 11 класс
Количество часов: 102 часов+3ч. резервных, 3 часа в неделю.
Алгебра и начала математического анализа: учеб. для 11 кл. общеобразоват. организаций: базовый и профильный уровни /С.М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. -М.: Просвещение, 2014.
|
№ |
Тема урока |
Кол. часов | Дата |
Повторение | ||
| По плану | По факту
| |||||
|
| Повторение | 4 |
|
|
| |
| 1 | Корень п-ой степени. Степень с рациональным показателем и ее свойства. | 1 |
|
| Свойства степеней | |
| 2 | Решение логарифмических уравнений и неравенств. | 1 |
|
| Свойства логарифма | |
| 3 | Решение тригонометрических уравнений. | 1 |
|
| Формулы корней тригономе- трических уравнений. | |
| 4 | Входной контроль | 1 |
|
|
| |
|
| Функции и их графики | 15 |
|
|
| |
| 5 | Элементарные функции | 1 |
|
| Монотонность функции. | |
| 6 | Область определения и область значения функции. Ограниченность функции | 1 |
|
| Нахождение значения функции в точке. | |
| 7 | Четность, нечетность, периодичность функций | 1 |
|
| Формулы движения. | |
| 8 | Четность, нечетность, периодичность функций | 1 |
|
| Средняя скорость движения | |
| 9 | Промежутки возрастания, убывания, знакопостоянства и нули функции | 1 |
|
| Свойства ригонометричес- ких функций. | |
| 10 | Исследование функций и построение их графиков элементарными методами | 1 |
|
| Возрастание и убывание функции. | |
| 11 | Исследование функций и построение их графиков элементарными методами | 1 |
|
| Элементарные функции и их графики. Приращение функции. | |
| 12 | Основные способы преобразования графиков | 1 |
|
| Область определения и область значения функции. | |
| 13 | Понятие предела функции. Понятие непрерывности функции. | 1 |
|
| Теоремы о производной функции. | |
| 14 | Односторонние пределы | 1 |
|
|
| |
| 15 | Свойства пределов функций | 1 |
|
|
| |
| 16 | Понятие непрерывности функции. | 1 |
|
|
| |
| 17-18 | Понятие обратной функции | 2 |
|
|
| |
| 19 | Контрольная работа №1 «Функции и их графики» | 1 |
|
| Решение неравенств | |
|
| Производная | 8 |
|
|
| |
| 20 | Понятие производной функции. Физический и геометрический смысл. |
|
|
| Метод интервалов. | |
| 21 | Производная суммы. Производная разности. |
|
|
|
| |
| 22,23 | Производная произведения. Производная частного | 2 |
|
| Алгоритм решения уравнений. | |
| 24 | Производные элементарных функций | 1 |
|
| Действия с рациональны- ми числами. | |
| 25,26 | Производная сложной функции | 2 |
|
| Возрастание и убывание функции. | |
| 27 | Контрольная работа №2. «Производная» |
|
|
| Локальный экстремум. | |
|
| Применение производной | 14 |
|
|
| |
| 28,29 | Максимум и минимум функции | 2 |
|
| Производные элементарных функций | |
| 30,31 | Уравнение касательной | 2 |
|
|
| |
| 32 | Вторая производная и ее физический смысл | 1 |
|
|
| |
| 33,34 | Возрастание и убывание функций | 2 |
|
| Производная суммы. Производная разности. | |
| 35,36 | Экстремум функции с единственной критической точкой. | 2 |
|
| Критические точки. | |
| 37,38 | Задачи на максимум и минимум. | 2 |
|
|
| |
| 39,40 | Построение графиков функций с применением производной. | 2 |
|
| Производная сложной функции | |
| 41 | Контрольная работа №3. «Применение производной» |
|
|
|
| |
|
| Первообразная и интеграл | 10 |
|
|
| |
| 42,43 | Первообразная. Таблица первообразных. | 2 |
|
| Общая схема исследования Функции. | |
| 44,45 | Основное свойство первообразной. | 2 |
|
| Таблица производных. | |
| 46 | Правила нахождения первообразной. | 1 |
|
| Теоремы о производных. | |
| 47 | Примеры задач, которые приводят к пониманию интеграла. Определение интеграла. | 1 |
|
| Возрастание и убывание функции. | |
| 48,49 | Формула Лейбница-Ньютона. | 2 |
|
| Площадь прямоугольника и трапеции. | |
| 50 | Применение интеграла к вычислению площадей плоских фигур. | 1 |
|
| Графики элементарных функций. | |
| 51 | Контрольная работа№4 | 1 |
|
| Таблица первообразных. | |
|
| Уравнения. Неравенства. Системы | 36 |
|
|
| |
| 52 | Равносильность уравнений и неравенств(4). Равносильные преобразования уравнений | 1 |
|
| Раскрытие скобок. | |
| 53 | Равносильные преобразования уравнений | 1 |
|
| Формулы сокращенного умножения. | |
| 54 | Равносильные преобразования неравенств | 1 |
|
| Правила нахождения первообразной. | |
| 55 | Равносильные преобразования неравенств | 1 |
|
| Формула Лейбница-Ньютона. | |
| 56 | Уравнения-следствия (7). Понятие уравнения-следствия | 1 |
|
| Решение уравнений. | |
| 57 | Возведение уравнения в чётную степень | 1 |
|
| Решение тригонометричес-ких уравнений. | |
| 58 | Возведение уравнения в чётную степень | 1 |
|
|
| |
| 59 | Потенцирование логарифмических уравнений | 1 |
|
| Свойства логарифмов. | |
| 60 | Другие преобразования, приводящие к уравнению-следствию | 1 |
|
| Показательные уравнения. | |
| 61 | Применение нескольких преобразований, приводящих к уравнению-следствию | 1 |
|
| Свойства неравенств. | |
| 62 | Применение нескольких преобразований, приводящих к уравнению-следствию | 1 |
|
|
| |
| 63 | Равносильность уравнений и неравенств системам(7). Основные понятия | 1 |
|
| Свойства показ-ной функции | |
| 64 | Решение уравнений с помощью систем | 1 |
|
|
| |
| 65 | Решение уравнений с помощью систем | 1 |
|
| Свойства логариф-ой функции | |
| 66 | Решение уравнений с помощью систем | 1 |
|
| Метод интервалов. | |
| 67 | Решение уравнений с помощью систем | 1 |
|
|
| |
| 68 | Решение неравенств с помощью систем | 1 |
|
|
| |
| 69 | Решение неравенств с помощью систем | 1 |
|
| Алгоритм решение неравенств. | |
| 70 | Решение неравенств с помощью систем | 1 |
|
|
| |
| 71 | Решение неравенств с помощью систем | 1 |
|
| Действительные числа. | |
| 72 | Равносильность уравнений на множествах(4). Основные понятия | 1 |
|
|
| |
| 73 | Возведение уравнения в чётную степень | 1 |
|
|
| |
| 74 | Возведение уравнения в чётную степень | 1 |
|
| Логарифмические уравнения. | |
| 75 |
| 1 |
|
| Таблица производных. | |
| 76 |
| 1 |
|
| Исследование функций. Построение графиков функций. | |
| 77 | Возведение неравенств в чётную степень | 1 |
|
| Свойства степеней | |
| 78 | Возведение неравенств в чётную степень | 1 |
|
| Свойства логарифма | |
| 79 | Метод промежутков для уравнений и неравенств(4). Уравнения с модулями | 1 |
|
| Формулы корней тригономе- трических уравнений. | |
| 80 | Неравенства с модулями | 1 |
|
|
| |
| 81 | Метод интервалов для непрерывных функций | 1 |
|
|
| |
| 82 | Контрольная работа №6 | 1 |
|
| Монотонность функции. | |
| 83 | Системы уравнений с несколькими неизвестными(7). Равносильность систем | 1 |
|
| Нахождение значения функции в точке. | |
| 84 | Равносильность систем | 1 |
|
| Формулы движения. | |
| 85 | Система-следствие | 1 |
|
| Средняя скорость движения | |
| 86 | Система-следствие | 1 |
|
| Свойства ригонометричес- ких функций. | |
| 87 | Метод замены неизвестных | 1 |
|
| Возрастание и убывание функции. | |
| 88 | Метод замены неизвестных | 1 |
|
| Элементарные функции и их графики. Приращение функции. | |
| 89 | Контрольная работа №7
| 1 |
|
|
| |
|
| Повторение курса алгебры за 10-11 классы. |
13 |
|
|
| |
| 90,91 | Тождественные преобразование выражений. | 2 |
|
|
| |
| 92,93 | Функции, свойства и их графики. | 2 |
|
|
| |
| 94,95 | Производная сложной, показательной, логарифмической и степенной функции.
| 2 |
|
|
| |
| 96,97 | Показательные и логарифмические уравнения и неравенства | 2 |
|
|
| |
| 98,99 | Тригонометрические уравнения и неравенства. | 2 |
|
|
| |
| 100 | Свойства вероятностей | 1 |
|
|
| |
| 101 | Итоговая контрольная работа | 1 |
|
|
| |
| 102 | Итоговый урок | 1 |
|
|
| |
| 103-105 | Резервный час | 3 |
|
|
| |
Просмотр содержимого документа
«кал.план. алг. 10»
Календарно-тематическое планирование
Алгебра и начала математического анализа 10 класс.
Количество часов: 105 часов из них 3ч. резерв, 3 часа в неделю.
Учебник: Алгебра и начала математического анализа 10 класс. С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин, - Москва «Просвещение», 2014
| № | Наименование раздела программы и количества часов |
Тема урока | Кол-во часов | Дата проведения |
Повторение | ||
| По плану | По факту | ||||||
| 1 | Повторение (3ч ) | Повторение Решение неравенств и систем неравенств. | 1 |
|
| Свойства неравенств. | |
| 2 |
| Повторение. Функции. Свойства и графики функций. Арифметическая и геометрическая прогрессии. | 1 |
|
| Функции и их графики. | |
| 3 |
| Входной срез по основной школы | 1 |
|
| Определение, формулы. | |
| 4 | Действительные числа (6ч) | Понятие действительного числа | 1 |
|
|
| |
| 5-6 |
| Множества чисел. Свойства действительных чисел | 2 |
|
|
| |
| 7 |
| Перестановки | 1 |
|
| Множество действительных чисел | |
| 8 |
| Размещения | 1 |
|
|
| |
| 9 |
| Сочетания | 1 |
|
|
| |
| 10 | Рациональные уравнения и неравенства (14ч) | Рациональные выражения | 1 |
|
| Решение неравенств. Определение модуля. | |
| 11 |
| Рациональные уравнения | 1 |
|
| Алгоритм решения уравнений. | |
| 12 |
| Рациональные уравнения | 1 |
|
| Равносильные уравнения. | |
| 13-14 |
| Системы рациональных уравнений. Самостоятельная Работа | 2 |
|
| Линейные уравнения. | |
| 15 |
| Метод интервалов решения неравенств | 1 |
|
| Раскрытие скобок. | |
| 16 |
| Метод интервалов решения неравенств | 1 |
|
| Формулы сокращенного умножения. | |
| 17-18 |
| Рациональные неравенства | 2 |
|
| Графическое решение уравнений и неравенств. | |
| 19-20 |
| Нестрогие неравенства | 2 |
|
|
| |
| 21-22 |
| Системы рациональных неравенств. Самостоятельная работа | 2 |
|
| Числовые функции и их свойства. | |
| 23 |
| Контрольная работа №1 | 1 |
|
| Квадратичная функция. | |
| 24-25 | Корень степени n (8ч) | Понятие функции и ее графика. Функция y= | 2 |
|
| Построение графиков функций. | |
| 26-27 |
| Понятие корня степени n. Корни четной и нечетной степенем | 2 |
|
| Свойства квадратного корня. | |
| 28 |
| Арифметический корень | 1 |
|
| Свойства арифметического квадратного корня. | |
| 29 |
| Свойства корней степени n | 1 |
|
| Область допустимых значений выражения | |
| 30 |
| Свойства корней степени n. Самостоятельная работа | 1 |
|
|
| |
| 31 |
| Контрольная работа № 2 | 1 |
|
|
| |
| 32 | Степень положительного числа (8ч) | Понятие степени с рациональным показателем | 1 |
|
| Формулы сокращенного умножения. | |
| 33-34 |
| Свойства степени с рациональным показателем | 2 |
|
| Определение степени с натуральным показателем. | |
| 35-36 |
| Понятие степени с иррациональным показателем | 2 |
|
| Свойства степеней с целым показателем. | |
| 37 |
| Показательная функция | 1 |
|
| Функция у = х2 и у = х3. | |
| 38 |
| Показательная функция. Тест | 1 |
|
| Сокращение дробей. | |
| 39 |
| Контрольная работа №3 | 1 |
|
|
| |
| 40 | Логарифмы (6ч) | Понятие логарифма | 1 |
|
|
| |
| 41 |
| Свойства логарифмов | 1 |
|
| Свойства показательной функции | |
| 42-43 |
| Свойства логарифмов. Тест | 2 |
|
|
| |
| 44-45 |
| Логарифмическая функция | 2 |
|
|
| |
| 46 | Показательные и логарифмические уравнения и неравенства (8ч) | Простейшие показательные уравнения | 1 |
|
| Свойства логарифма | |
| 47 |
| Простейшие логарифмические уравнения | 1 |
|
| Свойства логарифм. функций | |
| 48 |
| Уравнения, сводящиеся к простейшим заменой неизвестного | 1 |
|
| Правила решения уравнений.
| |
| 49 |
| Простейшие показательные неравенства | 1 |
|
|
| |
| 50 |
| Простейшие логарифмические неравенства | 1 |
|
|
| |
| 51 |
| Неравенства, сводящиеся к простейшим заменой неизвестного | 1 |
|
| Правила решения неравенств. | |
| 52 |
| Неравенства, сводящиеся к простейшим заменой неизвестного. Самостоятельная работа | 1 |
|
|
| |
| 53 |
| Контрольная работа №4 | 1 |
|
|
| |
| 54-55 | Синус и косинус угла (7) | Понятие угла. Радианная мера угла | 2 |
|
| Угол в геометрии. | |
| 56 |
| Определение синуса и косинуса угла | 1 |
|
| Определение тригонометрических функций через прям-ный треуг. | |
| 57-58 |
| Основные формулы для | 2 |
|
| Таблица значений | |
| 59-60 |
| Арксинус и арккосинус. Самостоятельная работа | 2 |
|
|
| |
| 61 | Тангенс и котангенс угла (4ч) | Определение тангенса и котангенса угла | 1 |
|
| Определение тригонометрических функций через единичную окружность. | |
| 62 |
| Основные формулы для tqα и ctqα | 1 |
|
| Преобразование тригонометрических выражений. | |
| 63 |
| Артангенс и арккотангенс. Тест | 1 |
|
|
| |
| 64 |
| Контрольная работа №5 | 1 |
|
|
| |
| 65-66 | Формулы сложения (10ч) | Косинус разности и косинус суммы двух углов | 2 |
|
|
| |
| 67-68 |
| Формулы для дополнительных углов | 2 |
|
|
| |
| 69-70 |
| Синус суммы и синус разности двух углов | 2 |
|
|
| |
| 71-72 |
| Сумма и разность синусов и косинусов | 2 |
|
|
| |
| 73-74 |
| Формулы двойных и половинных углов | 2 |
|
|
| |
| 75-76 | Тригонометрические функции числового аргумента (7ч) | Функция y = | 2 |
|
|
| |
| 77-78 |
| Функция y = | 2 |
|
| Угол в геометрии. | |
| 79 |
| Функция y = tg x | 1 |
|
| Таблица значений | |
| 80 |
| Функция y = ctg x | 1 |
|
|
| |
| 81 |
| Контрольная работа №6 | 1 |
|
|
| |
| 82-83 | Тригонометрические уравнения и неравенства (7ч) | Простейшие тригонометрические уравнения | 2 |
|
| Определение тригонометрических функций через прямоугольный треуг. | |
| 84-85 |
| Уравнения, сводящиеся к простейшим заменой неизвестного | 2 |
|
| Свойства функции у = sinx. | |
| 86 |
| Применение основных тригонометрических формул для решения уравнений | 1 |
|
| Свойства функции у = cosx. | |
| 87 |
| Применение основных тригонометрических формул для решения уравнений. Тест | 1 |
|
| Формула корней квадратного уравнения. | |
| 88 |
| Контрольная работа №7 | 1 |
|
|
| |
| 89-90 | Вероятность события (4ч) | Понятие вероятности события | 2 |
|
| Решение биквадратных уравнений. | |
| 91-92 |
| Свойства вероятностей | 2 |
|
|
| |
| 93 | Повторение (10ч) | Повторение. Рациональные уравнения и неравенства. | 1 |
|
|
| |
| 94 |
| Повторение. Корень степени п. | 1 |
|
|
| |
| 95 |
| Повторение. Степень положительного числа. | 1 |
|
|
| |
| 96 |
| Повторение. Простейшие показательные и логарифмические уравнения и неравенства. | 1 |
|
|
| |
| 97 |
| Повторение. Косинус, синус, тангенс и котангенс угла. | 1 |
|
|
| |
| 98 |
| Повторение. Формулы сложения. | 1 |
|
|
| |
| 99 |
| Повторение. Тригонометрические функции числового аргумента. | 1 |
|
|
| |
| 100 |
| Повторение. Тригонометрические уравнения и неравенства. | 1 |
|
|
| |
| 101 |
| Итоговая контрольная работа № 8. | 1 |
|
|
| |
| 102 |
| Итоовый урок | 1 |
|
|
| |
| 103-105 | Резерв (3ч) |
|
|
|
|
| |
1




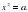 , п. 13
, п. 13 и ее график, п. 15
и ее график, п. 15 ,
, 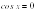 и т.п. Их решение нецелесообразно сводить к применению общих формул.
и т.п. Их решение нецелесообразно сводить к применению общих формул. Равносильность неравенств на множествах(3). Основные понятия
Равносильность неравенств на множествах(3). Основные понятия