Статья о результативном использовании современных педагогических технологий учителем математики
Романова Валентина Викторовна,
учитель высшей квалификационной категории,
МАОУ СШ № 2 г. Пестово Новгородской области
В современной школе перед каждым педагогом стоит задача – научить ребенка ориентироваться в реалиях технологичного, информационного общества, самостоятельно добывать знания, анализировать полученную информацию.
Актуальные педагогические технологии, которые помогают мне реализовать поставленные цели и добиться планируемых результатов:
1. Использование межпредметных связей (математика, физика, информатика, химия, география).
2. Использование активных форм познания (мозговой штурм, дискуссия, семинар).
3. Использование проектной деятельности (исследовательская деятельность).
4. Использование ИКТ: на уроке компьютер заменяет всю совокупность средств обучения, выполняя несколько ролей:
• запись на доске (тема урока, план, домашнее задание и т.д.);
• наглядность;
• таблицы и схемы;
• тесты;
• игры.
5. Использование рефлексии (оценка учеником своих учебных действий, соотнесение результата с целью).
6. Использование индивидуального подхода к учащимся.
7. Использование дифференцированных домашних заданий.
8. Использование технологической карты урока (оптимальная форма проектирования современного урока, позволяет тщательно планировать каждый этап деятельности, максимально полно отражать последовательность всех осуществляемых действий и операций, приводящих к намеченному результату и координацию, и синхронизацию действий всех субъектов педагогической деятельности, проект урока, составленный учителем с возможной корректировкой).
В педагогической практике использую системно-деятельностный подход как основу современного образовательного процесса (ФГОС). Он нацеливает на развитие личности ребёнка, на овладение системой метапредметных и предметных знаний, умений и навыков в процессе интенсивной учебной деятельности.
Только в процессе деятельности активизируется мозг, память, приобретается и накапливается опыт – идёт социализация обучающегося. Именно в процессе деятельности появляются открытия и радость от них, создается мотивация к дальнейшей деятельности. Таким образом, уместно говорить о творческой деятельности на уроке, в результате которой ученик не только открывает новое для себя знание, но и творчески реализует его.
Преимуществом деятельностного подхода является то, что он органично сочетается с различными современными образовательными технологиями.
Для повышения эффективности образовательного процесса при проведении уроков математики, использую следующие элементы современных образовательных технологий: модульной технологии, технологию проектного обучения, игровые технологии, здоровьесберегающие технологии, технологии развивающего обучения, технологии уровневой дифференциации, ИКТ технологии, которые позволяют организовывать проблемное обучение, способствуют интеграции знаний, дают возможность дифференцировать процесс обучения, формируют высокий уровень мотивации учащихся.
Технология проблемного обучения Проблемное обучение пронизывает весь курс математики. Практически каждый урок можно сделать проблемным. Ставится проблема, учащиеся подводятся к её решению.
В общем виде структура проблемного урока выглядит следующим образом:
1) подготовительный этап;
2) этап создания проблемной ситуации;
3) осознание учащимися темы или отдельного вопроса темы в виде учебной проблемы;
4) выдвижение гипотезы, предположений, обоснование гипотезы;
5) доказательство, решение и вывод по сформулированной учебной проблеме;
6) закрепление и обсуждение полученных данных, применение этих знаний в новых ситуациях
Приведу примеры создания проблемных ситуаци1.
Пример 1. Проблемная ситуация, когда обучающиеся сталкиваются с необходимостью использовать ранее усвоенные знания в новых практических условиях.
Я создаю эти условия не только для того, чтобы обучающиеся сумели применить свои знания на практике, но и для того, чтобы они при попытке использовать имеющиеся знания для решения практической задачи столкнулись с фактом их недостаточности. Осознание этого факта учащимися возбуждает познавательный интерес и стимулирует поиск новых знаний.
Алгебра, 8 класс, тема «Применение свойств неравенств с одной переменной».
В квадратном уравнении, написанном на доске, во время перемены кто-то стёр одно число:
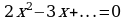 .
.
Я поставила на свободное место букву 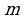 и, уравнение стало выглядеть так:
и, уравнение стало выглядеть так:
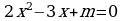 .
.
Ребятам было предложено самим найти значение 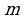 . Чтобы это стало возможным, сообщаю два следующих факта:
. Чтобы это стало возможным, сообщаю два следующих факта:
Вопросами о том, каковы коэффициенты и свободный член этого уравнения, от чего зависит количество корней квадратного уравнения, подвожу обучающихся к необходимости сначала составить дискриминант
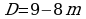 , а затем рассмотреть неравенство
, а затем рассмотреть неравенство 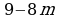 0. Решить само неравенство уже не составило труда: -8m-9, m
0. Решить само неравенство уже не составило труда: -8m-9, m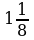 .
.
Значит, единственно возможное значение m – это 1.
Таким образом, перед уроком на доске было записано:
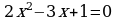 .
.
Пример 2. Проблемная ситуация возникает в том случае, если имеется противоречие между теоретически возможным путём решения задачи и практической неосуществимостью избранного способа.
Перед изучением темы «Описанные треугольники» (геометрия 8 класс) ребятам для обсуждения предлагаю задачу «Участок леса имеет треугольную форму. Нужно выбрать место для палатки, которая была бы на одинаковом расстоянии от границ участка леса».
Рассматриваем возможные варианты: идти от середины сторон леса или из углов участка. Но искомое место получается в разных точках. Возникает неожиданное затруднение.
Так, ещё до начала изучения новой темы была создана проблемная ситуация, которая помогла учащимся увидеть проблему, почувствовать необходимость её решения, выдвинуть предположения (гипотезы) и убедиться в их ошибочности.
Пример 3. Проблемная ситуация возникает тогда, когда имеется противоречие между практически достигнутым результатом и отсутствием у обучающихся знаний для его теоретического обоснования.
Геометрия, 8 класс, тема «Теорема Пифагора».
Перед изучением этой темы можно предложить учащимся следующее практическое задание:
Из частей двух квадратов, построенных на катетах прямоугольного треугольника, равных 3 и 4, составить новый квадрат.
Чтобы выполнить это задание, нужно разбить площадь квадратов на квадратные единицы и сравнить длину стороны полученного квадрата с гипотенузой.
В результате практической работы дети установили, что сторона нового квадрата равна длине гипотенузы и новый квадрат можно построить на этой гипотенузе.
Получен вывод о том, что площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов построенных на катетах.
Для проверки вывода можно предложить выполнить аналогичное построение для прямоугольного треугольника, катеты которого равны 2 и 4.
Разбивка квадратов на единичные квадраты и создание нового квадрата к выполнению этого задания не привели. Теперь возникла проблемная ситуация из-за того, что у обучающихся появилось сомнение относительно правильности полученного вывода. Возникшее затруднение вызвало у них желание и потребность выяснить, равна ли площадь квадрата, построенного на гипотенузе, сумме площадей квадратов, построенных на катетах. В данном случае потребность теоретического обоснования результатов учебно–практического задания подвела к формулировке теоремы Пифагора.
Пример 4. Проблемная ситуация возникает, если обучающиеся не знают способа решения поставленной задачи, не могут ответить на проблемный вопрос, дать объяснение новому факту в учебной и жизненной ситуации, т.е. в случае осознания обучающимися недостаточности прежних знаний для объяснения нового факта.
Алгебра, 7 класс, тема «Формулы сокращённого умножения».
Учитель: «Вчера по телевизору я смотрела передачу с участием экстрасенса, который произвёл на меня огромное впечатление. Я научилась быстро выполнять в уме операции над числами. Хотите я продемонстрирую свои способности?» Получив утвердительный ответ, предлагаю посоревноваться со мной в вычислениях.
І тур. Прошу кого-нибудь из ребят назвать два последовательных натуральных числа. Пусть школьник назовёт 129 и 130. Теперь я и класс вычисляем на скорость 1302 – 1292. Победителем становится учитель.
ІІ тур. Вновь обращаюсь к одному из учеников и прошу того назвать любые два числа. Пусть ученик назвал 1,43 и 2,51. Теперь класс и я соревнуемся при вычислении значения выражения:
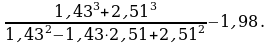
Понятно, что учитель, пользуясь формулами сокращённого умножения, легко побеждает в соревновании. Изменяя задания, неизменно побеждая, учитель, в конце концов, добьётся от ребят фразы типа: «Вы знаете какой – то простой способ!»
«Да, действительно, я знаю такой способ, и Вы узнаете его на этом уроке и сможете быстро выполнять такие вычисления».
Игровые технологии
Игровые технологии на уроках математики помогают сделать процесс обучения увлекательным и мотивирующим для обучающихся. Вот несколько примеров игровых технологий, которые я использую:
| № п/п | Игровая технология | Краткое описание | Учебная тема |
| 1 | Дидактические игры | Игры, специально разработанные для обучения. Они могут включать карточки с заданиями, головоломки, викторины и другие элементы. | 6 класс. Игры: "Математическое домино", "Угадай число". Тема: «Действия с отрицательными и положительными числами». |
| 2 | Настольные игры | Настольные игры, созданные совместно с детьми на математические темы, помогают стать отличным дополнением к учебному процессу. | 5 класс. Игры: «Детектив», «Математическая трасса». Тема: «НОД и НОК натуральных чисел». |
| 3 | Головоломки и загадки | Использую задачи-головоломки, такие как магические квадраты или задачи на логику. В текущем учебном году использовала книгу: Гайштут А.Г. Математика в логических упражнениях.- К.: Рад. шк., 1985. Задания из книги развивают критическое мышление и умение решать нестандартные задачи. | Во всех классах, на разные учебные темы. Например, 8 класс, «Системы линейных уравнений». Вместо знака ? вставьте число. 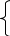 8х+3у=5 8х+3у=5 8a7 b -8 9х-11у=20
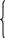 2х+7у=13 2х+7у=13 2ab9 ? 5х-у=14
|
| 4 | Ролевые игры | В ролевых играх учащиеся принимают на себя роли и решают математические задачи в контексте определенной ситуации. Например, игра «Продавцы» помогает научить основам арифметики и процентов, когда ученики торгуют товарами, рассчитывают прибыль и налоги.
| 5-6 классы. Игры: «Продавцы», «Менеджер магазина», учат основам арифметики и процентов, когда ученики торгуют товарами, рассчитывают скидки, прибыль и налоги. |
| 5 | Соревнования и турниры | Соревнования между командами учеников, где они соревнуются в решении математических задач.
| 8 класс. Игра: «Математический бой». Тема: « Решение задач по формуле классической вероятности». |
| 6 | Брейн - ринги и викторины | Викторины с вопросами по математике стимулируют соревновательный дух и помогают закрепить знания. | Все классы, неделя математики. Темы: «История математики», «Занимательные задачи». |
| 7 | Математические квесты | Квест — это серия заданий, где учащиеся проходят через различные этапы, решая математические задачи, чтобы продвигаться дальше.
| 9-е классы. Математический квест «Путешествие по задачам ОГЭ». |
| 8 | Интерактивные доски и приложения | Использование интерактивной доски позволяет внедрять динамические элементы в обучение, помогает визуализировать геометрические фигуры и функции, делая изучение геометрии и алгебры более наглядным. | Использую интерактивное учебное пособие «Наглядная математика» с 5 по 11 класс. |
| 9 | Компьютерные симуляции физических явлений и процессов. | Современные образовательные платформы предлагают интерактивные игры, которые помогают визуализировать математические концепции. Например, игры на построение графиков функций, решение уравнений или задачи на вероятность.
| Использую в 10-11 классах учебное пособие «Цифровая лаборатория по математике (профильный уровень)». |
Эти методы делают уроки математики интересными и разнообразными, помогают ученикам лучше усваивать материал и развивают любовь к предмету.
Здоровьесберегающие технологии
Одной из современных задач образования является сохранение и укрепление здоровья детей. Обновленные ФГОС определяют эту задачу как одну из приоритетных. Здоровье, по концепции стандартов, понимается как совокупность нескольких составных среди которых физическое, психическое, духовное, социальное здоровье.
При организации учебной деятельности я уделяю внимание следующим факторам:
1) результат любого труда, а особенно умственного, зависит от настроения, от психологического климата (в недоброжелательной обстановке утомление наступает быстрее), поэтому на уроке создаю обстановку доброжелательности, положительного эмоционального настроя, ситуации успеха, применяю эмоциональные разрядки;
2) тщательно планирую организацию учебного труда для предупреждения утомляемости; при планировании урока предусматриваю смену деятельности, чередую различные виды активности: интеллектуальная – эмоциональная – двигательная;
3) на уроках рассматриваем задачи, которые непосредственно связаны с понятиями «здоровый образ жизни», «правильное питание», «экология»; Примеры:
Задача 1.
Вычислите, какую часть лимона необходимо съедать ежесуточно, для того чтобы восполнить потребность организма в витамине С.
В расчетах следует принять, что масса лимона равна 100 г; содержание витамина С в лимоне составляет 0,5%. Суточная потребность взрослого человека в витамине С – 100мг.
Задача 2.
Один стакан цельного молока содержит 288 мг кальция. Сколько нужно выпивать в день молока для снабжения вашего организма достаточным количеством этого элемента? (Суточная потребность – 800 мг Са)
4) соблюдение санитарно-гигиенических условий обучения (наличие оптимального светового и теплового режима в кабинете, условий безопасности, соответствующих СанПиНам мебели, оборудования, оптимальной окраски стен и т.д.). Организовано проветривание до и после занятий и частичное - на переменах. Проводится влажная уборка кабинета;
5) проведение физкультминуток и динамических пауз на уроках:
- в виде игры: улыбнуться, как в день рождения, когда тебе дарят подарок или нахмуриться, как учитель, когда плохо написали контрольную работу;
- в рамках изучаемых тем урока: если называю неправильную дробь – встаньте на носочки, поднимите руки верх, если правильную – опустите руки вниз, расслабьтесь (5 – класс); нарисуйте рукой график линейной функции при различных значения коэффициента возрастания – убывания (7-8 класс);
- универсальные: крепко закрыть глаза на 3-5 секунд, а затем открывать их на такое же время, повторять 6-8 раз.
Использую в работе материалы санитарно - просветительской программы «Основы здорового питания (для детей школьного возраста)».
В данной статье я рассмотрела основные современные педагогические технологии, которые применяю.
Основные выводы:
Использование современных образовательных технологий позволяет повысить мотивацию учащихся, сделать процесс обучения интересным и увлекательным, способствует развитию самостоятельности и критического мышления.
Дифференцированный подход помогает учитывать индивидуальные особенности каждого ученика, обеспечивая доступность материала и возможность успешного освоения программы каждым учащимся.
Интерактивные методы способствуют активному вовлечению учеников в учебный процесс, формируют коммуникативные компетенции и умение работать в команде.
Информационные технологии позволяют значительно расширить возможности представления учебного материала, повышают наглядность и качество усвоения знаний.
Таким образом, внедрение современных педагогических технологий является необходимым условием повышения качества образования, развития познавательной активности школьников и формирования необходимых компетенций в области математики.
Применение инновационных подходов требует от учителя постоянного профессионального роста, творческого подхода и готовности экспериментировать, что позволит обеспечить высокую результативность образовательного процесса.
Романова В.В., 2025







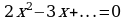 .
.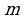 и, уравнение стало выглядеть так:
и, уравнение стало выглядеть так: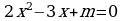 .
.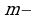 число натуральное;
число натуральное;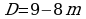 , а затем рассмотреть неравенство
, а затем рассмотреть неравенство 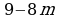 0. Решить само неравенство уже не составило труда: -8m-9, m
0. Решить само неравенство уже не составило труда: -8m-9, m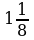 .
.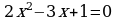 .
.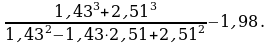
 8х+3у=5
8х+3у=5 2х+7у=13
2х+7у=13









