Умножение и деление обыкновенных дробей

Для дальнейшего решения заданий с алгебраическими выражениями необходимо ориентироваться в решении дробных. Поэтому целью данного урока является повторение основных действий с дробями. Неотъемлемой частью решения дробных выражений является знания свойств дроби при отнимании, сложении, сокращении, умножении и делении.

Правило умножения дроби на дробь.

При умножении дроби   на дробь   необходимо перемножить числители, и результат поставить в числитель, а также перемножить знаменатели и результат поставить в знаменатель. Получаем: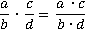 

Правило деления дроби на дробь.

Существует два способа деления дроби на дробь.

1-й способ: Для того, чтобы разделить дробь  на дробь  , надо дробь 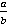 умножить на обратную дробь  , т.е. на  .

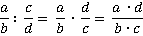
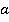2-й способ: Для того чтобы разделить дробь  на дробь  , надо числитель   первой дроби умножить на знаменатель  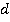 второй дроби и получить числитель  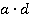 искомой дроби, знаменатель  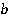 первой дроби умножить на числитель  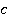 второй дроби и получить знаменатель  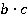 искомой дроби: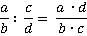 

Правило умножения дроби на число.

При умножении дроби   на число 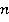  необходимо числитель  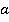 умножить на число  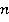, а знаменатель  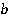 оставить неизменным. Данное правило подтверждается еще тем, что любое число  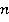 можно представить в виде дроби  .

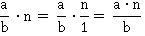
Пример 8: Умножить дробь   на число 7.

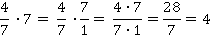
Правило деления дроби на число.

При делении дроби  на число 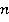  необходимо число  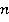 представить в виде дроби   и потом использовать правило деления дроби на дробь.

Пример 9: Разделить дробь   на число 7.

.
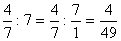