Диагностика математических способностей

ДИАГНОСТИКА

МАТЕМАТИЧЕСКИХ СПОСОБНОСТЕЙ

Доклад учителя Акимовой Елены Ибраимовны

Диагностика математических способностей

В неразрывной связи с проблемой развития математических способностей находится проблема их диагностики у школьников, главной задачей которой является установление качественного своеобразия мыслительной деятельности ученика в процессе решения математических задач, т.е стиля его мышления.
У школьников индивидуальные качества мышления выражены слабо, о стиле математического мышления учащихся , например 5-6 классов, можно говорить лишь условно. Но уже и у них на определенном уровне математического развития начинают проявляться своеобразие и «тенденция» в использовании приемов мысли, методов решения задач, в привлечении образов воображения, в особенностях интуиции и догадки.
Психологи установили, что раннее проявление «своего» стиля математического мышления - признак математической одаренности. Следовательно, возможно раннее выявление математических способностей школьников - одна из важнейших задач обучения математике.

Способности проявляются в деятельности.
Основной вид математической деятельности школьников - это решение задач. Но подбор задач для диагностики математических способностей сопряжен с определенными трудностями. Такими задачами могут быть особого вида задания - тесты, выполнение которых позволило бы установить качественные особенности и уровень развития математических способностей ученика, выявить стиль его математического мышления.
К задачам - тестам диагностики математических способностей следует предъявлять такие требования:
1) условие задачи не должно ориентировать на способы решения, оно должно быть нейтральным по отношению к ним;
2)потенциально задачи должны содержать множество различных подходов и способов решения;
3) задачи должны служить не только диагностике способностей , но и их формированию.

Привожу примерный тест (с решениями), характерной особенностью которого является многоаспектность в подходе к его решению.

Задача. Прилетели галки, сели на палки, по одной галке на каждую палку, при этом одной галке не хватило палки. Если бы на каждую палку сели бы по две галки, то одна палка оказалась бы незанятой. Сколько было палок и сколько было галок?

Решение1. (алгоритмический подход). Вводим обозначения неизвестных: палок было х, а галок было у. Из первого условия составляем уравнение: х= у-1; Из второго условия следует: 2(х-1)=у. Получаем систему:

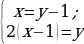
решение которой приводит к ответу: х=3, у=4.

Решение2. (наглядно-образный подход). Пусть имелось какое-то число палок. Изобразим их и посадим на каждую палку по одной галке. При этом, согласно условию, одной галке не хватит палки. Она летает.
Теперь посадим летающую галку на первую палку, а с последней палки пересадим галку на вторую(слева) палку. При этом одна палка осталась незанятой… Дальше процесс пересадки галок не может продолжаться, так как будут свободными уже не одна палка, а две,что противоречит условию.
Очевидно, что для того чтобы удовлетворить условию задачи, необходимо, чтобы палок было 3, а галок 4. Задача решена.

Решение 3. (использован метод проб и ошибок с проявлением склонности к счетно-вычислительным операциям). Допустим, что палок было 10, тогда галок-11. Но тут сразу же возникает противоречие: 11 галок нельзя рассадить по две на каждую палку. Следовательно, галок было нечетное число, а палок на единицу меньше- нечетное число. Пусть палок было 7, а галок 8. Тога по две галки займут 8:2=4 палки, что не на одну, а на 3 палки меньше, чем 7. Пусть палок 5, галок 6. Тогда по две галки разместятся на 3 палках. Опять противоречия: две палки остаются незанятыми, а не одна. Пусть палок 3, галок 4. Тогда по две галки сядут на две палки, а одна палка (3-2=1) останется незанятой. Получилось. Следовательно, палок было 3, галок 4.

Решение 4. (логическое, с использованием наглядности).
Очевидно, что число галок четное (это непосредственно следует из второго условия), т.е 2n( n∈ N) , а число палок на единицу меньше, т.е 2n-1. Если на каждую палку сядут по две галки, то они займут n палок.
Имеем: 2n больше 2n -1 на 1 и 2n-1 больше n на 1. Это можно изобразить наглядно в виде диаграммы.

2n 2n-1 n 2n n

Из диаграммы ясно, что если 2n больше 2n-1 на 1 и 2n-1 больше n на 1, то 2 n больше n на 2. Откуда следует, что n=2. Тогда 2-1=3, 2n=4.
Число галок 4, число палок 3.

Решение 5.(логический подход с использованием на завершающем этапе решения метода испытаний).
Очевидно, что число галок четное, т.е. 2n ( n ∈ N) , а число палок , исходя из первого условия, нечетное, т.е. 2n-1 . Если на каждую палку сядут по две галки, то они займут 2 n: 2= n палок. Число n- четное, так как на 1 меньше нечетного числа (второе условие) 2n-1. Пусть n=2 m(m ∈ N), тогда 2n-1= 4m-1. Откуда следует , что число галок 2n=4 кратно четырем; а число палок 2n-1 = 4m-1 при делении на 4 дает в остатки 3. Выпишем эти числа попарно; 3 и 4, 7и8, 11 и 12, 15 и 16 и т.д. Путем испытаний убеждаемся, что только первая пара чисел 3 и 4 удовлетворяет всем условиям задачи. Следовательно, палок было 3, а галок 4.

Решение 6. (индуктивный подход; при исследовании использованы метод математической индукции).
Допустим, что была всего одна палка. Тогда, согласно первому условию, галок было две. Если на каждую палку сядут по две галки, то свободных палок не окажется, что противоречит второму условию. Этот вариант отпадает.
Допустим, что палок было две, тогда галок должно быть три. Но три галки не могут сесть по две на каждую палку, что требуется вторым условием. Следовательно, и этот вариант отпадает .
Допустим, что палок было 3, тогда галок было 4. Первое условие удовлетворяется. Второе условие также удовлетворяется. Следовательно, числа 3(палки) и 4(галки) являются решением задачи.
Но может быть, задача имеет и другие решения. По – видимому, надо попробовать решить задачу в общем виде. Применим метод математической индукции. Допустим , что палок было n , тогда галок должна быть n+1. Для n=3 условие задачи удовлетворяются. Допустим, существует такое натуральное число kчто для n =3+ k условие задачи тоже выполняется. Тогда, согласно второму условию, будем иметь :
2 (k+3-1)= 3+ k+1; откуда k=0. Следовательно, решение задачи единственное.

Выводы:
1) Важно выявить не общую склонность ученика к математике(«ученик любит математику»), а установить присущий ему образ мышления, его стиль;

2)развитие математических способностей ученика должно осуществляться с учетом индивидуальных особенностей мышления;

3) формирование стиля математического мышления должно быть целенаправленным с ориентацией на ту область человеческой деятельности или профессию, которая наиболее близко отвечает математическим интересам, складу ума ученика.