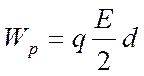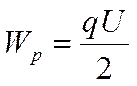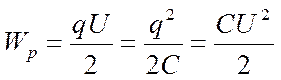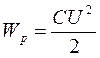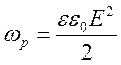Энергия заряженного конденсатора

ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА. ПРИМЕНЕНИЕ КОНДЕНСАТОРОВ

Как и любая система заряжен­ных тел, конденсатор обладает энер­гией. Вычислить энергию заряжен­ного плоского конденсатора с одно­родным полем внутри него не­сложно.

Энергия заряженного конденса­тора. 

Для того чтобы зарядить конденсатор, нужно совершить рабо­ту по разделению положительных и отрицательных зарядов. Согласно закону сохранения энергии эта ра­бота равна энергии конденсатора. В том, что заряженный конденсатор обладает энергией, можно убедиться, если разрядить его через цепь, со­держащую лампу накаливания, рас­считанную на напряжение в не­сколько вольт. При раз­рядке конденсатора лампа вспыхи­вает. Энергия конденсатора пре­вращается в другие формы: тепло­вую, световую.

Выведем формулу для энергии плоского конденсатора.

Напряженность поля, созданного зарядом одной из пластин, равна Е/2, где Е — напряженность поля в конденсаторе. В однородном поле одной пластины находится заряд q, распределенный по поверхности дру­гой пластины (рис. 5). Согласно формуле W_p = qEd. для потенциальной энергии заряда в однородном поле энергия конденсатора равна:

(1)

где q — заряд конденсатора, a d — расстояние между пластинами.

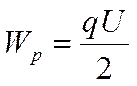
Так как Ed = U, где U — разность потенциалов между обкладка­ми конденсатора, то его энергия равна:

(2)

Эта энергия равна работе, ко­торую совершит электрическое поле при сближении пластин вплот­ную.

Заменив в формуле (2) раз­ность потенциалов или заряд с по­мощью выражения для элек­троемкости конденсатора, получим

(3)

Можно доказать, что эти форму­лы справедливы для энергии любого конденсатора, а не только для плос­кого.

Энергия электрического поля.

Согласно теории близкодействия вся энергия взаимодействия заряженных тел сконцентрирована в электриче­ском поле этих тел. Значит, энергия может быть выражена через основную характеристику поля — напря­женность.

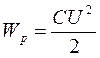
Так как напряженность электри­ческого поля прямо пропорциональ­на разности потенциалов

(U = Ed), то согласно формуле

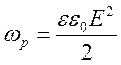
энергия конденсатора прямо пропор­циональна напряженности электри­ческого поля внутри него: W_p ~ E². Детальный расчет дает следующее значение для энергии поля, приходя­щейся на единицу объема, т.е. для плотности энергии:

(4)

где ε₀ — электрическая постоянная

Применение конденсаторов.

Энер­гия конденсатора обычно не очень велика — не более сотен джоулей. К тому же она не сохраняется долго из-за неизбежной утечки заряда. Поэтому заряженные конденсаторы не могут заменить, например, акку­муляторы в качестве источников электрической энергии.

Но это совсем не означает, что конденсаторы как накопители энергии не получили практического при­менения. Они имеют одно важное свойство: конденсаторы могут на­капливать энергию более или менее длительное время, а при разрядке через цепь малого сопротивления они отдают энергию почти мгновенно. Именно это свойство используют широко на практике.

Лампа-вспышка, применяемая в фотографии, питается электрическим током разряда конденсатора, заря­жаемого предварительно специаль­ной батареей. Возбуждение кванто­вых источников света — лазеров осу­ществляется с помощью газораз­рядной трубки, вспышка которой происходит при разрядке батареи конденсаторов большой электроем­кости.

Однако основное применение кон­денсаторы находят в радиотехнике. С этим вы познакомитесь в XI классе.

Энергия конденсатора пропор­циональна его электроемкости и квадрату напряжения между плас­тинами. Вся эта энергия сосредото­чена в электрическом поле. Плот­ность энергии поля пропорциональна квадрату напряженности поля.