Эвристические исследовательские задания по математике
Исследовательские задания позволяют ученикам отыскивать знания о реальных объектах математики с помощью эвристического наблюдения, поиска фактов, постановку вопросов, выдвижения гипотез, сравнения разных версий, формулирование понятий, эмоционально-образное познание, «вчувствование» в состояние объекта и др. Расширяют кругозор и способствуют развитию математической зоркости учащихся, их аналитических способностей. Такие задания могут стать началом исследовательского проекта ученика.
В ходе выполнения исследовательских заданий у школьников развиваются и совершенствуются когнитивные качества, необходимые человеку в процессе познания окружающей действительности, такие как: любознательность, эрудированность, вдумчивость, аргументированность, способность к анализу и синтезу, умение использовать различные формы доказательств.
Результатами работы над исследовательскими заданиями могут быть: версия, гипотеза, доказательство, теория, выявленная закономерность, классификация и т.д.
При оценивании задания основное внимание уделяется оценке сформированности исследовательских умений: ставить цель, выдвигать и проверять гипотезу, проводить доказательные рассуждения.
1. Фибоначчи, трибоначчи, тетраначчи...
Если вы знаете, как построить последовательность чисел Фибоначчи, то легко догадаетесь, как продолжить ряд чисел трибоначчи (1, 1, 2, 4, 7, 13, 24, 44, 81, …). Эти числа были так названы блестящим молодым математиком, Марком Фейнбергом, написавшим статью о них в журнал Fibonacci Quarterly (октябрь 1963 г.) в возрасте 14 лет. Последоватеельность тетраначчи постройте самостоятельно. Сравните эти три последовательности. Найдите как можно больше фактов попарного сходства и отличия.
2. Числа в стихах.
Японские знаменитые стихотворения хайку содержат 17 слогов в трёх строках, разделённых по схеме 5-7-5. Есть ли числа, скрытые в стихах, которые вы читаете? Проведите исследования нескольких современных стихотворений. Результаты запишите в таблицу и сделайте вывод о связи чисел и гармонии слов.
| Автор | Название | Что считали? | Результаты подсчётов |
|
|
|
|
|
3. Советы для главнокомандующего.
На город Олимпийск периодически нападает флот инопланетян. Флот состоит из нескольких космических кораблей, каждый из которых имеет форму равнобедренного прямоугольного треугольника. Сторона корабля, которая проходит по гипотенузе располагается строго с юга на север. Флот застывает на небольшое время в таком положении на разной высоте над городом. За это время нужно нанести урон инопланетной армии, пустив из некоторой точки поверхности Земли лазерный луч вертикально вверх. Пущенный так луч прожигает насквозь все вражеские корабли, через которые он проходит (даже если задевает корабль по границе).
Помогите военным властям города в расчетах ударов по вражеским войскам. Для этого проведите исследование возможного расположения из 2-х, 3-х, 4-х инопланетных кораблей, задав координатную плоскость. Какое количество лазерных установок понадобится в рассмотренных случаях? Предложите командованию советы, как быстро определить количество установок и место их расположения.
4. Значение беспорядка.
Любите ли вы порядок? Посмотрите вокруг себя, например, на свою книжную полку с учебниками. Их порядок хранит какие-то ваши интересы, пристрастия и… конечно, любовь или нелюбовь к порядку. Пронумеруем каждый учебник своим номером. Запишите варианты расстановки учебников, которые удобны для вас, назовём это расположение «порядком» (в виде последовательности номеров). Все другие положения назовем «беспорядком». Рассмотрите математические свойства последовательностей, представляющих «идеальный порядок» и «полный беспорядок». Какие закономерности «порядка» и «беспорядка» вы обнаружили?
5. Простая последовательность.
Выпишите последовательность простых чисел в порядке возрастания. Создайте новую последовательность, каждый элемент которой равен разности двух последовательных чисел из первой последовательности. Повторите это несколько раз (из большего числа вычитая меньшее). Перечислите, какие закономерности можно увидеть в получаемых последовательностях? Поэкспериментируйте с последовательностью простых чисел, предлагая другие правила построения новых последовательностей. Результаты каких опытов показались вам наиболее интересными, почему? Приведите 2-3 примера новых последовательностей, опишите принципы их построения и увиденные закономерности.
6. Закон Бенфорда.
Физик Бенфорд проанализировал около 20 таблиц, среди которых были данные о площади бассейна 335 рек, удельной теплоёмкости и молекулярном весе тысяч химических соединений и, в том числе, номера домов первых 342 лиц, указанных в справочнике. В результате оказалось, что первая цифра в исследованных числах, единица встречается с вероятностью не 1/9 как следовало бы ожидать (цифр всего девять), а примерно в 30% случаев. Давайте проверим этот загадочный закон! Для этого возьмите газету и проанализируйте все встречающиеся в статьях числа (по закону числа должны быть взяты из реальной жизни).
Заполните таблицу:
| Первая цифра числа | Количество встретившихся чисел | Процент от общего числа проверенных чисел |
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|
| 5 |
|
|
| 6 |
|
|
| 7 |
|
|
| 8 |
|
|
| 9 |
|
|
Подтверждает ли ваше исследование закон Бенфорда? Почему?
7. Конь-крокодил.
«Крокодилом» называется фигура, ход которой заключается в прыжке на m клеток по вертикали или по горизонтали, и потом на n клеток в перпендикулярном направлении (например, шахматный конь – это «крокодил» с m = 1, n = 2). Исследуйте поведение «крокодила» для различных n и m. Сможет ли крокодил «обойти» все клетки шахматной доски 8 х 8 при:
1) n = 2, m = 2;
2) n = 1, m = 3;
3) n = 2, m = 4?
Если не сможет – докажите это, если сможет – приведите пример.
8. Секрет бумаги.
Посмотрите множество объектов, созданных искусными мастерами оригами на сайте http:/www.loveorigami.info/. Но, во вкладке «Математика» всего лишь три статьи. Попробуем исправить положение. На самом деле, преобразуя лист бумаги, в результате получается набор фигур, который складывается в какой-то объект. Выберите для исследования одну или несколько работ (можно использовать работы, приведённые ниже). Проанализируйте, какие геометрические тела, фигуры в результате сложились в единый образ, какие из них положены в основу, какие являются второстепенными, но придают законченность образу и шарм, есть ли какие-то закономерности в их использовании. Перечислите те геометрические факты, которые вас удивили.



Автор: Хадживара Г. Автор: Спрунг К. Автор: Traditional
9. Тройка, семерка, туз.
Числа 1, 3 и 7 занимали умы русских поэтов. Можно вспомнить Велимира Хлебникова и его константу 317, описанную в Теории Времени, или знаменитые «тройку, семёрку, туз» Пушкина. Исследуйте различные числа, получающиеся комбинацией этих трёх поистине магических цифр 317, 371, 173, 137, 713, 731. Какие открытия вам удалось сделать?
10. Параметр.
Существуют уравнения, которые в зависимости от параметра могут иметь или не иметь решения. Например, уравнение 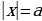 не имеет решений при всех a
не имеет решений при всех a
1) имеют единственное решение для каждого значения параметра a;
2) при любом значении параметра a не имеют решения;
3) имеют бесконечно много решений при любом значении параметра a;
4) свой вариант.
11. Именной треугольник.
Математика знает не мало знаменитых треугольников. Это и пифагоров треугольник, и треугольник Паскаля, треугольник Серпинского и даже невозможный треугольник Пенроуза! Треугольники Паскаля и Серпинского почти братья. Раскрыть секрет их построения не сложно (сделайте это сами, или обратитесь за помощью в Интернет). А для того, чтобы один превратить в другой достаточно чёрной краской покрасить нечётные числа, а места чётных – оставить белыми (обязательно проверьте это утверждение!).

Ваша задача – предложить свой числовой треугольник, указав способ его построения.
Придумайте правило превращения «треугольника имени вас» в геометрического собрата!
12. Следопыт.
Попробуем перенести след от числовой последовательности на сетку ученической тетради. Число – это расстояние до очередного поворота по часовой стрелке. На рисунке изображён след простейшей арифметической прогрессии: 1, 2, 3, 4, 5, …
Приведите исследование следов 3-5 арифметических или геометрических прогрессий для квадратной и треугольной сеток. У какой из прогрессий след самый интересный? Проанализируйте результат на предмет зависимости между следами и свойствами последовательностей. Сделайте вывод о практическом применении вашего исследования.
13. Пересечения.
В пространстве дано N точек, попарно соединенных отрезками. Какое наибольшее число из этих отрезков может пересечь плоскость, не проходящую ни через одну из данных точек? Сформулируйте и решите аналогичную задачу на плоскости.
14. Необитаемый остров.
На острове есть горы и впадины, а ещё перевалы – по ним можно ходить из впадины во впадину. Если число гор равно Г, число впадин – В, то, сколько может быть перевалов?
15. Письмо Абелю.
Норвежский математик Абель в 1896 году писал своему другу: «Можешь ли ты вообразить нечто более ужасное, чем утверждение, что 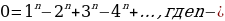 положительное целое число?». И далее продолжал: «В математике вряд ли есть хоть один бесконечный ряд, сумма которого была бы строго определена». Что бы вы ответили Абелю на месте его друга?
положительное целое число?». И далее продолжал: «В математике вряд ли есть хоть один бесконечный ряд, сумма которого была бы строго определена». Что бы вы ответили Абелю на месте его друга?
16. Многогранник.
Швейцарский математик Леонард Эйлер, проживший почти всю жизнь в России, обнаружил удивительное соотношение между числом вершин (В), рёбер (Р) и граней (Г) любого многогранника: В + Г – Р = 2. Попытайтесь исследовать один или несколько многогранников (можно склеить из бумаги) и отыщите другие математические свойства своих фигур. Ваша цель – путем наблюдений, измерений, подсчётов, математических опытов, эвристических приёмов, обнаружить как можно больше свойств многогранника. Возможно, что ваше исследование завершится не соотношением, аналогичным формуле Эйлера, а чем-либо иным, например, сформулированной проблемой, гипотезой или закономерностью. Результаты исследования изложите по следующему плану: объект, факт (что увидел); вопрос (по отношению к увиденному факту); действие (что сделал, чтобы ответить на вопрос), версия ответа, выводы.
17. Свойства угла.
Углом иногда называют часть плоскости, заключенной между двумя лучами с общим началом. Если принять это определение, то получается, что углы, отличающиеся друг от друга на 360 градусов (добавляется лишний оборот луча), оказываются равными. В самом деле, часть плоскости, которая заключена между лучами угла в 450 градусов и угла в 810 градусов – одна и та же. Это вся плоскость! Как разрешить данное противоречие?
18. Снежный ком.
Иногда о чём-нибудь говорят, что оно «растёт, как снежный ком». А какой функцией можно описать рост снежного кома? От каких аргументов она зависит? Нарисуйте график её поведения в зависимости от различных аргументов. При каких аргументах функция будет линейной, а при каких – периодичной? Приведите примеры проявления и использования функции в жизни.
19. В каждой шутке есть доля шутки.
В одной из своих задач математик И. Акулич спрятал одно из свойств четырёхугольника: «Отметим на плоскости несколько точек. Соединим каждые две из них отрезком и назовём середины этих отрезков точками второго поколения. Таким же образом, соединив всевозможными отрезками точки второго поколения, получим точки третьего поколения, потом – четвёртого и так далее. Докажите, что если ни во втором, ни в третьем поколениях никакую точку мы не отмечали дважды, то и ни в каком следующем поколении никакую точку не придётся отмечать дважды». Какое свойство четырёхугольника использует автор? Предложите свою задачу с решением, которое незаметно, на первый взгляд опирается на свойство какой-то фигуры.
Литература:
Математика, 9-11 классы. Сборник эвристических заданий. Учебно-методическое пособие / под ред. А.В.Хуторского. – М.: Издательство «Эйдос», Издательство Института образования человека, 2013.










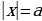 не имеет решений при всех a
не имеет решений при всех a 
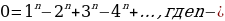 положительное целое число?». И далее продолжал: «В математике вряд ли есть хоть один бесконечный ряд, сумма которого была бы строго определена». Что бы вы ответили Абелю на месте его друга?
положительное целое число?». И далее продолжал: «В математике вряд ли есть хоть один бесконечный ряд, сумма которого была бы строго определена». Что бы вы ответили Абелю на месте его друга?









