Формирование математической грамотности учащихся

ФОРМИРОВАНИЕ МАТЕМАТИЧЕСКОЙ ГРАМОТНОСТИ УЧАЩИХСЯ

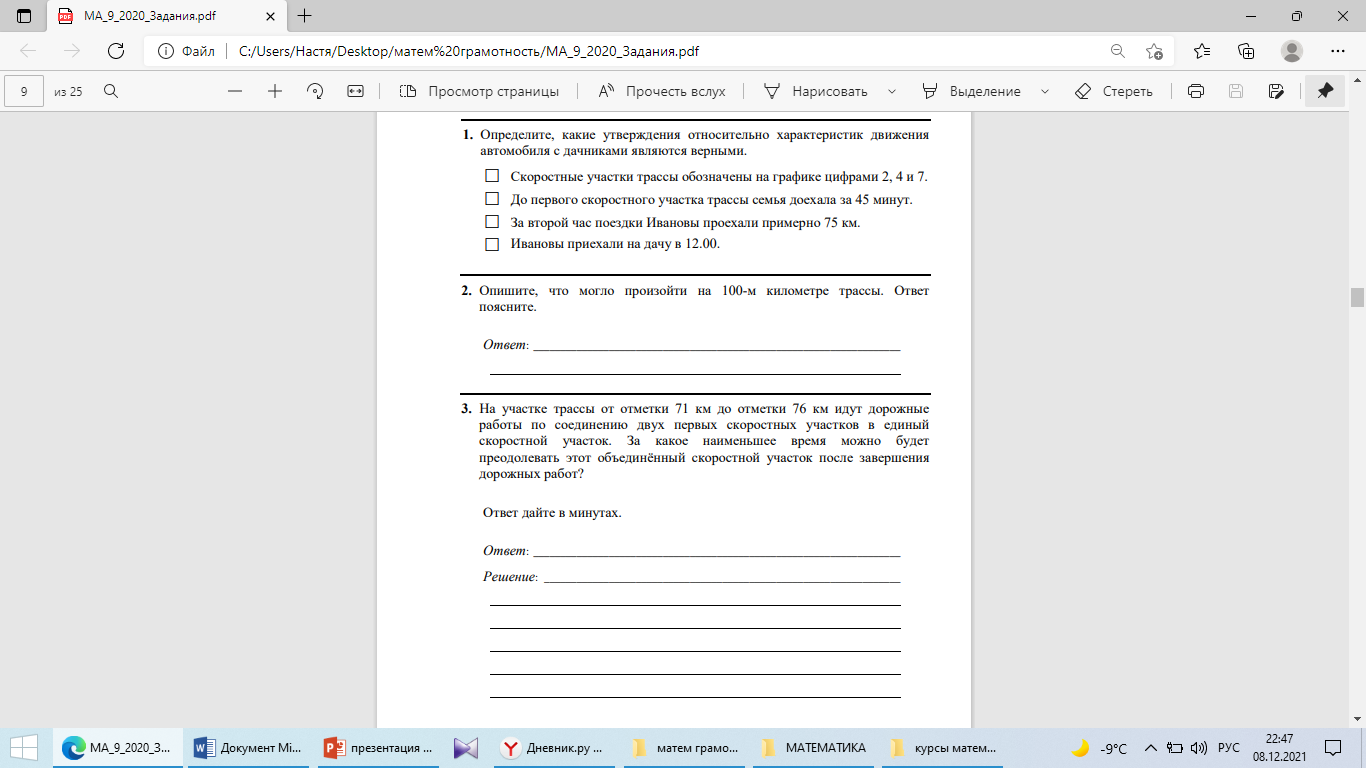
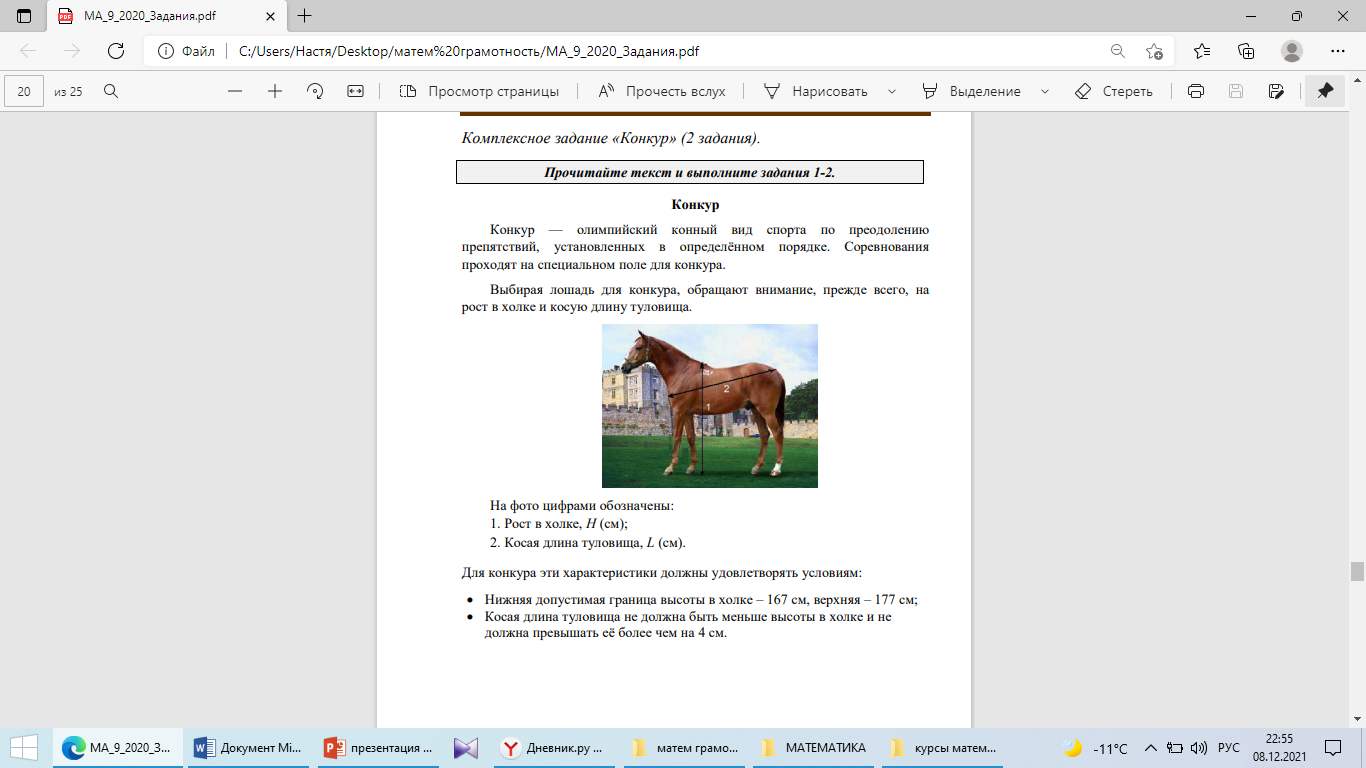
Детей надо учить тому,

что пригодится им, когда они вырастут.
Аристипп

Формирование функционально грамотных людей является одной из важнейших задач современной школы. Введение в российских школах Федерального государственного образовательного стандарта определяет актуальность понятия «функциональная грамотность», в основе которой - умение личности ставить и изменять цели и задачи своей деятельности, планировать, осуществлять ее контроль и оценку, действовать в ситуации неопределенности в решении актуальных проблем.

Согласно Концепции федеральных государственных образовательных стандартов общего образования на первый план наряду с общей грамотностью (т.е. усвоение системы знаний, умений и навыков, составляющих инструментальную основу компетенций учащегося) выступает «формирование умения учиться как компетенции, обеспечивающей овладение новыми компетенциями; включение содержания обучения в контекст решения значимых жизненных задач», а также личностное, социальное, познавательное и коммуникативное развитие, что обусловлено изменением общей парадигмы образования.

В основе развития функциональной грамотности лежит, прежде всего, освоение предметных знаний, понятий, ведущих идей. Такие международные оценочные исследования, как оценка математической и естественнонаучной грамотности учащихся 4 и 8-х классов (TIMSS) и международная программа оценки учебных достижений 15-летних учащихся (PISA) основаны на концепции функциональной грамотности. Они оценивают, на сколько обучающиеся способны использовать знания, умения и навыки, приобретенные в школе, для решения жизненных задач в различных сферах человеческой деятельности, а также в социальных отношениях.

Одной из составляющей функциональной грамотности является математическая грамотность учащихся. Математическая грамотность – это способность человека определять и понимать роль математики в мире, в котором он живёт, высказывать обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину.
Учащиеся, которые овладеют математической грамотностью, способны:

• распознавать проблемы, возникающие в окружающей действительности и решаемые средствами математики;

• формулировать эти проблемы на языке математики;

• решать проблемы, используя математические факты и методы;

• анализировать использованные методы решения;

• интерпретировать полученные результаты с учетом поставленной проблемы;

• формулировать и записывать результаты решения.

Согласно этому основное внимание нужно уделять проверке способности учащихся использовать математические знания в разнообразных ситуациях, требующих для своего решения различных подходов.

Учащиеся должны уметь решать любые поставленные перед ними задачи. В зависимости от сложности задания выделены три уровня математической компетентности: уровень воспроизведения, уровень установления связей, уровень рассуждений.

Первый уровень (уровень воспроизведения) — это прямое применение в знакомой ситуации известных фактов, стандартных приемов, распознавание математических объектов и свойств, выполнение стандартных процедур, применение известных алгоритмов и технических навыков, работа со стандартными, знакомыми выражениями и формулами, непосредственное выполнение вычислений.

Второй уровень (уровень установления связей) строится на репродуктивной деятельности по решению задач, которые, хотя и не являются типичными, но все же знакомы учащимся или выходят за рамки известного лишь в очень малой степени. Содержание задачи подсказывает, материал какого раздела математики надо использовать и какие известные методы применить. Обычно в этих задачах присутствует больше требований к интерпретации решения, они предполагают установление связей между разными представлениями ситуации, описанной в задаче, или установление связей между данными в условии задач.

Третий уровень (уровень рассуждений) строится как развитие предыдущего уровня. Для решения задач этого уровня требуются определенная интуиция, размышления и творчество в выборе математического инструментария, интегрирование знаний из разных разделов курса математики, самостоятельная разработка алгоритма действий. Задания, как правило, включают больше данных, от учащихся часто требуется найти закономерность, провести обобщение и объяснить или обосновать полученные результаты.

Математическая грамотность включает в себя математические компетентности, которые можно формировать через специально разработанную систему задач:

1 группа – задачи, в которых требуется воспроизвести факты и методы, выполнить вычисления;

2 группа – задачи, в которых требуется установить связи и интегрировать материал из разных областей математики;

3 группа – задачи, в которых требуется выделить в жизненных ситуациях проблему, решаемую средствами математики, построить модель решения.

Приведенное выше описание математической грамотности в международных исследованиях и уровней ее овладения (уровней компетентности) дает возможность прийти к главному выводу о том, что приоритетным направлением усовершенствования математического образования является обеспечение математической грамотности высокого уровня компетентности. Именно обеспечение практической и прикладной направленности математического образования и составляет сущность компетентностного подхода к обучению математике. Имеется в виду направленность на решение жизненных проблем, к действиям в реальных условиях.

Формирование функциональной математической грамотности требует изменений к содержанию деятельности на уроке. Ученик может научиться действовать только в процессе самого действия, а ежедневная работа учителя на уроке, образовательные технологии, которые он выбирает, формируют функциональную грамотность.

Формируя новые компетенции при работе с обучающимися нужно планировать работу применения новых знаний, нового способа по выработанному алгоритму. Для этого надо предлагать ученикам решить ситуационные, практико-ориентированные задания, задачи открытого типа.

Классификация задач:

• Предметные задачи: в условии описывается предметная ситуация, для решения которой требуется установление и использование знаний конкретного учебного предмета, которые изучались на разных этапах и в разных его разделах.

• Межпредметные задачи: в условии описана ситуация на языке одной из предметных областей с использованием языка другой предметной области. Для решения нужно применять знания из соответствующих областей; требуется исследование условия с точки зрения выделенных предметных областей, а также поиск недостающих данных.   

• Ситуационные задачи: не связаны с непосредственным повседневным опытом обучающегося, но они помогают увидеть и понять, как и где могут быть полезны в будущем знания из различных предметных областей.

• Практико-ориентированные задачи: в условии описана такая ситуация, с которой подросток встречается в повседневной жизни. Для того, чтобы решить задачу, нужно мобилизовать не только теоретические знания из конкретной или разных предметных областей, но и применить знания, приобретенные из повседневного опыта самого обучающегося. Данные в задаче берутся из реальной действительности.

Практико-ориентированные задачи являются одним из важнейших элементов в развитии математической грамотности учащихся.

Особен­ности практико-ориентированных задач, отличающие их от других математических задач:

1. -значимость (общекультурная, познавательная, про­фессиональная, социальная) получаемого результата, что обеспечивает познавательную мотивацию учащегося);

   1. -условие задачи сформулировано как сюжет, ситу­ация или проблема, для разрешения которой необходимо использовать знания из разных разделов основного пред­мета — математики, из другого предмета или из жизни, на которые нет явного указания в тексте задачи;

2. -информация и данные в задаче могут быть пред­ставлены в различной форме (рисунок, таблица, схема, диаграмма, график и т. д.), что потребует распознавания объектов;

1. -указание (явное или неявное) области применения результата решения;

1. -нестандартная структура (когда некоторые эле­менты не определены);

2. -наличие избыточных, недостающих и противоре­чивых данных в условии, делающих его объемным;

-наличие нескольких способов решения, причем, не все из них могут быть известны учащимся.

Решение практико-ориентированных задач является лучшим тренажером математической грамотности.

Практико-ориентированные задачи нужно включать в учебный про­цесс с 5 класса вплоть до государственной итоговой аттестации. Эти задачи можно применять на различных этапах урока: актуализация знаний, из­учение нового материала, закрепление, систематизация и обобщение.

Взаимодействуя с окружа­ющей действительностью, дети лучше усваивают материал и приобретают первичный опыт использования матема­тических знаний в быту, повышают свой уровень мате­матической грамотности.

Могу от­метить положительные моменты, свя­занные с решением практико-ориентированных задач:

1. -повышение мотивации учащихся к получению новых знаний;

2. -более осмысленное освоение нового материала;

3. -стремление к творческой и исследовательской дея­тельности;

4. -приобретение навыков самостоятельной и коллек­тивной работы;

5. -осознание учащимися важности математики, как науки, приносящей реальную пользу в повседневной жизни.

Систематическое решение практико-ориенти­рованных задач на уроках математики, несомненно, дает хорошие результаты, повышая уровень матема­тической грамотности учащихся. Решение практико-ориентированных задач готовит их не только к успешной сдаче ОГЭ, где первые пять заданий яв­ляются практико-ориентированными, но и дает ценные навыки по применению математических знаний в ре­альной жизни.

Таким образом, в целях развития и повышения качества математического образования необходимо продолжить поиски новых методов и форм обучения, делая акцент на формирование математической грамотности учащихся.

Выделю некоторые проблемы, возникающие при формировании функциональной грамотности на уроках математики.

1) учащиеся не умеют выделять существенную информацию, вопрос и данные, важные для решения задачи.

2) не могут сформулировать задачу так, чтобы найти математический аппарат, с помощью которого можно решить привычную математическую задачу. Оценить математические связи между событиями.

3) и у них вызывает затруднения обратный перевод с математического языка на язык решаемой проблемной задачи. Иногда учащиеся, получив ответ при решении задачи, не думают, возможен ли такой результат в реальности. И получают в ответе: отрицательную сторону  квадрата, отрицательную скорость движения  или не целое количество людей и т.п. Частая ошибка    при решении задач на наибольшее ( наименьшее) с целыми ответами, не понимание по смыслу задачи, в какой именно проводиться округление к большему значению, а в какой к меньшему.

И в заключении хочу показать Модель формирования и развития грамотности.

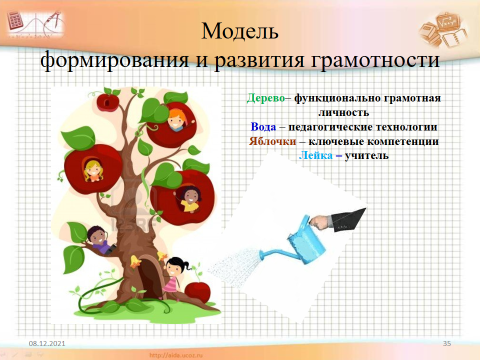
приложение