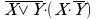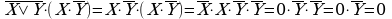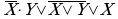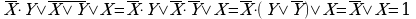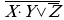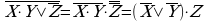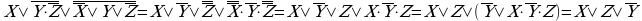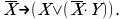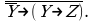Тема «Формулы и законы логики. Равносильные преобразования»
План лекции:
Основные понятия алгебры логики
Формулы и законы логики
Равносильные преобразования
Примеры
Самостоятельная работа
Основные понятия алгебры логики
Логическая переменная — это простое высказывание, содержащее только одну мысль.
Логическая функция - составное высказывание, которое содержит несколько простых мыслей, соединенных между собой с помощью логических операций.
Логические операции — логическое действие
Мы рассмотрели с вами 5 логических операций – инверсия, конъюнкция, дизъюнкция, импликация и эквиваленция.
Рассмотрим еще три логических операций – стрелка Пирса, штрих Шеффера, сложение по модулю два.
Стрелка Пирса (функция Вебба) X Y – функция, принимающая значение истина, когда X – ложно и Y – ложно.
Y – функция, принимающая значение истина, когда X – ложно и Y – ложно.
| X | Y | X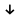 Y Y |
| 1 | 1 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 0 | 0 | 1 |
Штрих Шеффера 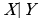 - функция, принимающая значение ложь, если X – истинно и Y – истинно.
- функция, принимающая значение ложь, если X – истинно и Y – истинно.
| X | Y | 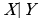
|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
Сложение по модулю два (или сумма Жегалкина) 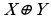 - функция, принимающая значение истинно, когда X и Y принимают противоположные значения.
- функция, принимающая значение истинно, когда X и Y принимают противоположные значения.
| X | Y | 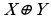
|
| 1 | 1 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
Если составное высказывание (логическую функцию) выразить в виде формулы, в которую войдут логические переменные и знаки логических операций, то получится логическое выражение, значение которого можно вычислить.
Вычислять истинность можно по таблицам истинности
Табличный способ определения истинности сложного высказывания имеет ограниченное применение, т.к. при увеличении числа логических переменных приходится перебирать слишком много вариантов.
Есть случаи, где используют способ приведения формул к нормальной форме.
Формула имеет нормальную форму, если в ней отсутствуют знаки эквивалентности, импликации, двойного отрицания, при этом знаки отрицания находятся только при переменных, также отсутствуют и операции - стрелка Пирса, штрих Шеффера, сложение по модулю два. Нормальной формы можно добиться, если применить законы логики и упростить по ним данную функцию
Формулы и законы логики
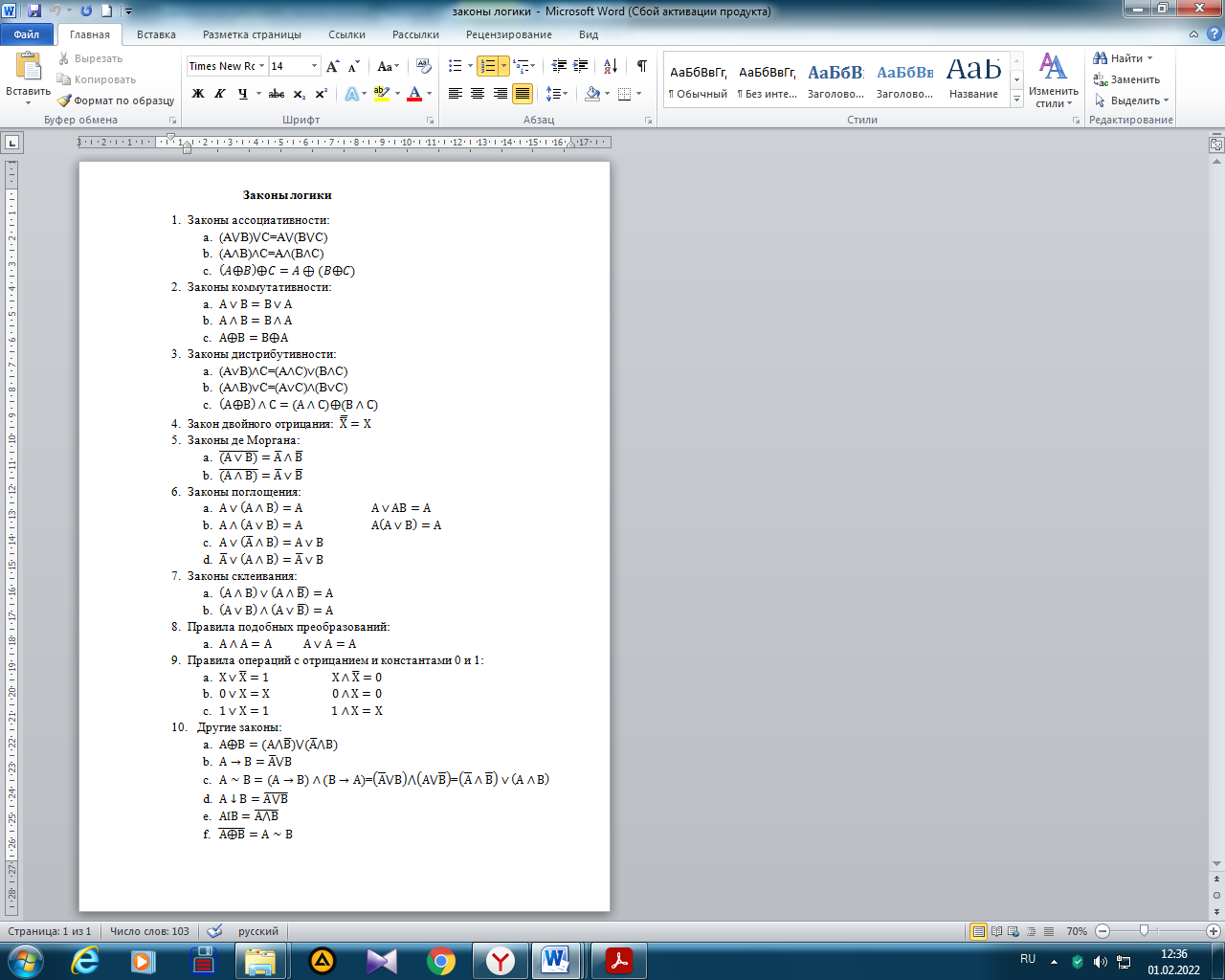
Равносильные преобразования
Сложные высказывания (формулы) А и В называются равносильными, если их истинностные значения совпадают для любых наборов истинностных значений простейших высказываний, входящих в эти формулы.
Равносильность формул будем обозначать знаком 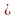 , а запись А
, а запись А 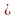 В означает, что формулы А и В равносильны.
В означает, что формулы А и В равносильны.
Для упрощения записи формул принят ряд соглашений. Скобки можно опускать, придерживаясь следующего порядка действий: конъюнкция выполняется раньше, чем все остальные операции, дизъюнкция выполняется раньше, чем импликация и эквивалентность. Если над формулой стоит знак отрицания, то скобки тоже опускаются. Убирать по законам логики лучше начинать по обратному приоритету или в скобках.
Приоритет операций:
Действия в скобках
Действия, стоящие под инверсией
Инверсия над высказыванием
Конъюнкция, штрих Шеффера, стрелка Пирса
Дизъюнкция
Импликация
Эквиваленция, сложение по модулю 2
Примеры
Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
Упростить формулу 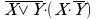
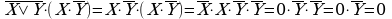
Здесь законы алгебры логики применялись в следующей последовательности: правило де Моргана, дистрибутивный закон, правило операций с отрицанием и правило операций с константами;
Упростить формулу 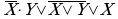
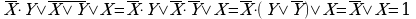
Применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией;
Упростить формулу 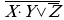
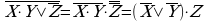
Сначала добиваемся, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого дважды применяем правило де Моргана; затем используем закон двойного отрицания;
К отрицаниям неэлементарных формул применяется правило де Моргана; используются законы двойного отрицания и склеивания;
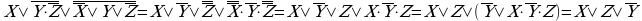
Из этих примеров видно, что при упрощении логических формул не всегда очевидно, какой из законов алгебры логики следует применить на том или ином шаге.
Самостоятельная работа
Переписать лекцию в тетрадь, кроме законов логики и пояснений к примерам, Законы логики распечатать и вклеить. Примеры переписать, а над каждым равно поставить номер закона, который использовался в тот момент. Прислать фото
Упростить следующие формулы по законам логики. Над каждым равно ставить номер закона, который используется:
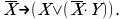
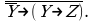







 Y – функция, принимающая значение истина, когда X – ложно и Y – ложно.
Y – функция, принимающая значение истина, когда X – ложно и Y – ложно. 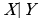 - функция, принимающая значение ложь, если X – истинно и Y – истинно.
- функция, принимающая значение ложь, если X – истинно и Y – истинно.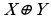 - функция, принимающая значение истинно, когда X и Y принимают противоположные значения.
- функция, принимающая значение истинно, когда X и Y принимают противоположные значения.
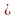 , а запись А
, а запись А