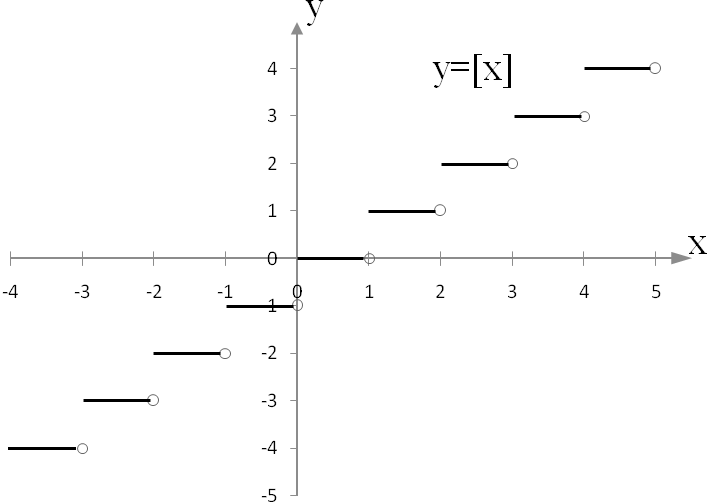Функции y= [x] и y={x} и их графики.

Урок № 4 – 5

Тема. Функции y= [x] и y={x} и их графики.

Тип. Комбинированный.

Цели.

• Обеспечить усвоение учащимися определение новых функций целая часть числа y= [x] и дробная часть числа y={x};

• ознакомить учеников с их графиками;

• продолжить работу по формированию умений строить графики функций с модулем;

• воспитывать у учащихся графическую культуру, аккуратность;

• развивать алгоритмическое и логическое мышление при решении нестандартных задач;

Оборудование: программа «MF – 2.0».

ХОД УРОКА

І. . Организационный момент.

II. Актуализация опорных знаний. Фронтальный опрос.

1) Алгоритм построения функций, если y=f(x)- известна

1. f(x-b)

2. f(kx)

3. kf(x)

4. f(-x)

5. f(|x|)

6. |f(x)|

7. 2) Составьте алгоритм построения графика функции.

y=af(bx+c)+d

III. Мотивация изучения материала.

К этому моменту мы чертили нестандартные графики функций и все функции были непрерывны. Сегодня мы узнаем, что есть функции, графики которых можно начертить не отрывая карандаша от бумаги. Что это за функции.

IV. Усвоение новых знаний.

Целой частью числа х называется наибольшее целое число, не превышающее данное х.

Обозначают [x].

По значению имеем [x]≤х

То есть [3,7]=3, [-0,5]=0, [-2,4]=-3, [-√3]= -2.

Теперь рассмотрим функцию y= [x]

x€ [0;1), то y=0 x€ [-1;0), то y=-1

x€[1;2), то y=1 x€ [-2;-1), то y=-2

и др.

Тогда график функции приобретает вид.

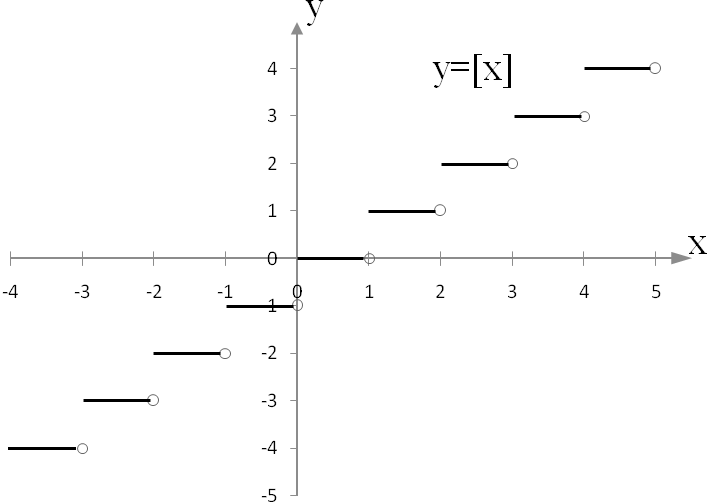
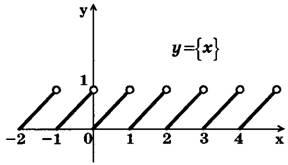
Дробной частью называют разницу х-[x] и обозначают {x}.

По значениям: {x}= х - [x]. Понятно, что {x}≥0 и 0≤{x}

То есть {2,5}=0,5 {-4,65}=0,35 {5}=0;

Теперь рассмотрена функция y={x}.

x€ [0;1), y€ [0;1).

x€ [1;2), y€ [0;1).

График приобретает вид

V. Закрепление изученного.

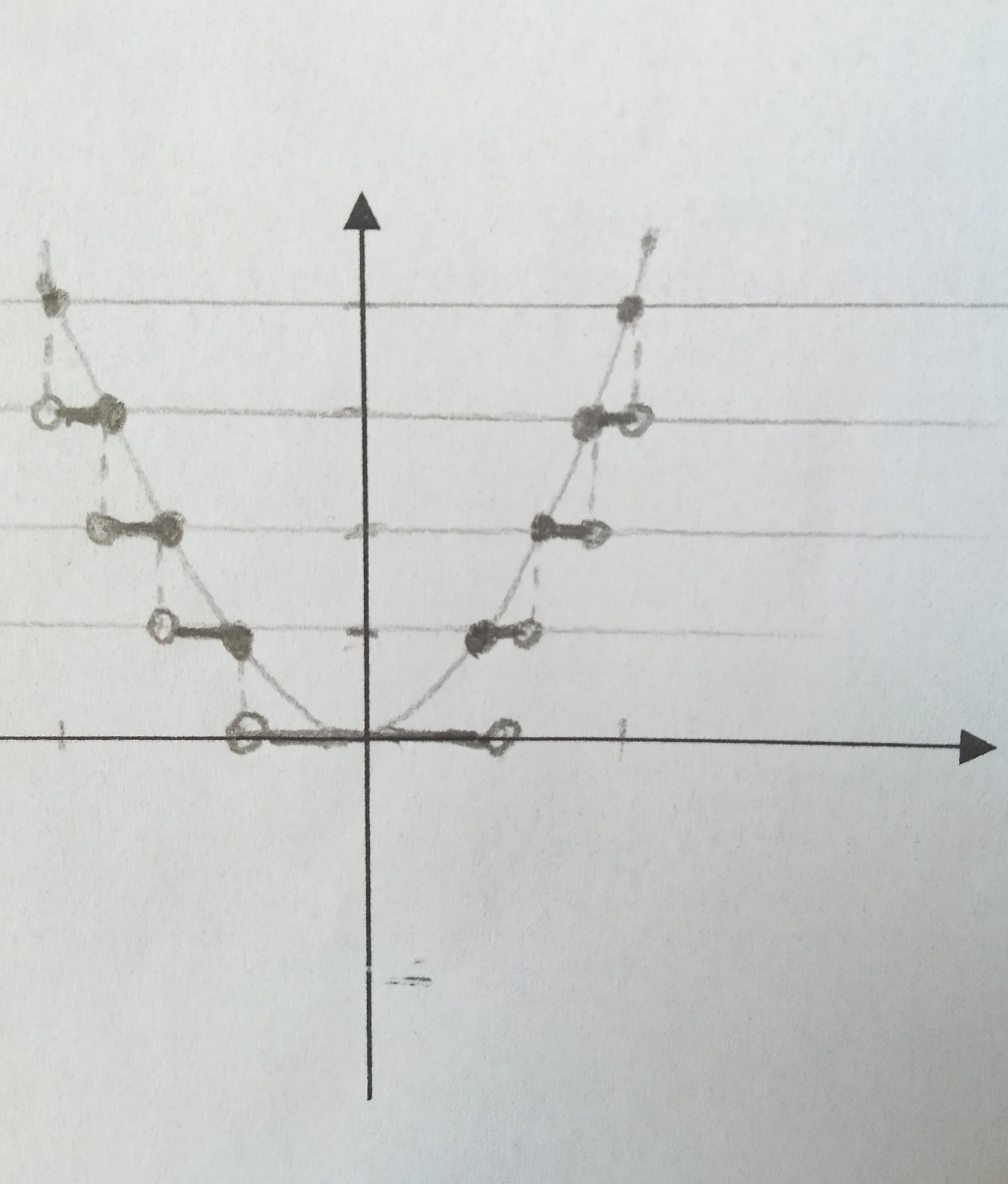
Построить график функции у=[x²] .

Алгоритм построения написано на доске.

1) сначала у=x² .

2) проводим прямые y=n, n€Ζ.

3) Рассматриваем полосы между прямыми у=n и у=n+1.

Точки пересечения прямых у=n, у=n + 1 с графиком у=х² принадлежат у=[x²], поскольку их ординаты - целые числа;

4) Другие точки получим, как проекции точек графики у=х² прямую у=n.

VI. Практическая работа. (Решение нестандартных задач)

Пример.

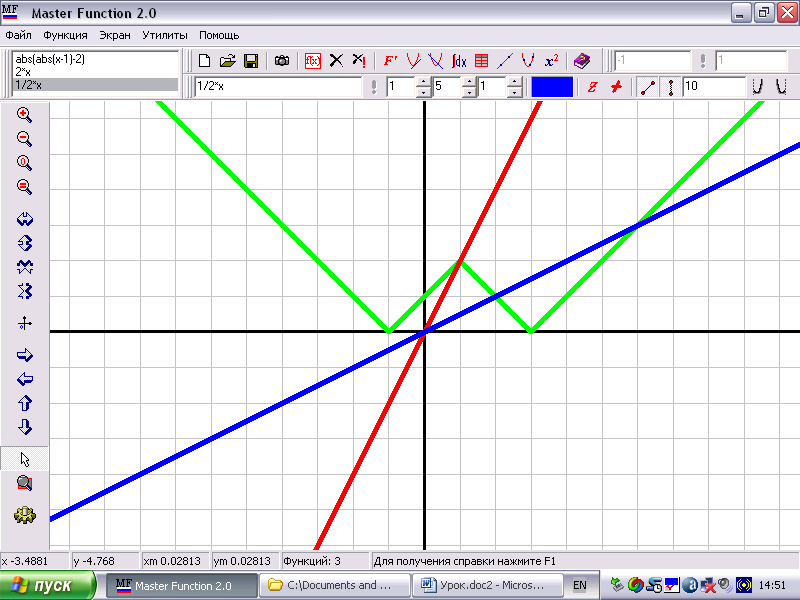
I. Найти значение параметра a€R, для каждого из которых уравнение

||x-1|-2| =ax имеет четыре решения (учащиеся работают с программой «MF – 2.0».) Алгоритм решения.

1. Построим график функции у= ||x-1|-2|

2. Строим график прямой пропорциональности у = ах, а € R

3. Из взаимного расположения графиков делаем вывод.

4. Ответ

II. Ученики в паре получают задание.

Карточка № 1

Найти значение параметра а, для каждого из которых уравнение

| x² + 6x + 5| = a -3 имеет не менее, чем три решения.

Алгоритм.

1. Выразим а через х. Имеем |х² +6х +3| +3 =а.

2. Чертим график в тетради и на экране

y=|x² + 6x + 3|+3 = |(x+3)² -4|+3

y=a – пучок параллельных прямых

3. Делаем вывод.

4. Учащиеся записывают ответ в тетради

5. Учитель проверяет задание, оценивание

VIІ. Подведение итогов: беседа с классом.

Домашнее задание

1) Построить график у= |6x² -5|х|+2|

2) Построить график функции у=[x] ²

3) Найти все значения параметра а, для каждого из которых уравнение

|x² -2x |=а имеет не меньше, чем два решения.

5