Градусная и радианная меры углов и дуг.

Оценка: определяют результаты своей работы на уроке

Синтез: используют градусную и радианную меры в решении задач

Анализ: проверить и получить формулы связи градусной и радианной мерами

Применение: демонстрируют применение формул связи градусной и радианной мерами

Понимание: обсуждают определение угла в 1 радиан и формулы, устанавливающие связь между радианной и градусной мерами углов.

Знание: рассказывают определения и формулы связи градусной и радианной мерами

Учебно-воспитательные задачи:

Образовательная:

Познакомиться с определением угла в 1 радиан и формулами, устанавливающими связь между радианным и градусным измерением углов,

обеспечить усвоение новых знаний по данной теме, сформировать навыки применения знаний по данной теме

Развивающая: развитие способности выражать мысли, познавательных способностей, формирование алгоритмического мышления, расширение кругозора

Воспитательная: способствовать выявлению, раскрытию способностей учащихся, возбуждать интерес к предмету, побуждать учащихся к применению полученных знаний

Результаты обучения:

Учащиеся знают градусную и радианную меры измерения углов

Учащиеся умеют: применять градусную и радианную меры в решении задач, ясно выражать мысли, участвовать в дискуссии, умеют слушать и слышать

Этапы урока

Содержание этапа

Оргмомент.

Задачи: обеспечить нормальную внешнюю обстановку на уроке, психологически подготовить детей к общению

Приветствие

Проверка подготовленности к уроку

Организация внимания школьников

Ознакомление с планом проведения урока

Проверка домашнего задания.

Задачи: установить правильность, полноту и осознанность выполнения всеми учащимися домашнего задания, выявить пробелы в знаниях, устранить в ходе проверки обнаруженные пробелы

Выявление степени усвоения заданного учебного материала

Фронтальный опрос.

Ликвидация обнаруженных недостатков.

Вызов.

Задачи: обеспечить включение школьников в совместную деятельность по определению целей учебного занятия.

Сообщение темы урока

Формулируют цели: сформировать навыки применения знаний по данной теме

Актуализация знаний и умений

Задачи: психологическая подготовка ученика: сосредоточение внимания, осознание значимости предстоящей деятельности, возбуждение интереса к уроку; учащиеся воспроизводят известные им знания, осознают их, обобщают факты, связывают старые знания с новыми условиями, с новыми данными и т.д. 

Преподаватель приветствует обучающихся, проверяет их готовность к уроку.

Дорогие ребята!

Известно, что 21 век называют веком информации. Почему? Во - первых, потому, что уже сейчас, в начале века, объем новой информации удваивается каждые 5-6 лет. Во - вторых, ученые предсказывают, что в будущем власть будет в руках тех, кто владеет информацией. Это значит, что для успешной и счастливой жизни человеку нужно постоянно пополнять свой багаж знаний. Для этого необходимо овладеть умениями работы с учебной литературой, понимать, перерабатывать, применять, хранить в памяти и передавать другим.

Сегодня вам представлена возможность самостоятельно изучить тему "Радианная мера угла". Мне кажется, вам будет удобно работать вдвоем для того, чтобы не только проверить друг друга, но и помочь исправить ошибки, ликвидировать пробелы в знаниях.

Каждый путешественник знает цель своего движения. У нас это учебная цель: к концу урока вы должны знать формулы, устанавливающие связь между различными измерениями углов и уметь ими пользоваться и применять радианную меру углов при решении задач.

Градусная мера угла.

К градусам мы как-то привыкли. Геометрию худо-бедно проходили... Да и в жизни частенько встречаемся с фразой "повернул на 180 градусов", например. Ответьте, что такое градус?

Градусы придумали в Древнем Вавилоне. Давненько это было... Веков 40 назад... И придумали просто. Взяли и разбили окружность на 360 равных частей. 1 градус - это 1/360 часть окружности. И всё. Могли разбить на 100 частей. Или на 1000. Но разбили на 360. Кстати, почему именно на 360? Чем 360 лучше 100? 100, вроде, как-то ровнее... Попробуйте ответить на этот вопрос.

Где-то в то же время, в Древнем Египте мучились другим вопросом. Во сколько раз длина окружности больше длины её диаметра? И так измеряли, и этак... Всё получалось немного больше трёх. Но они, египтяне не виноваты. После них ещё веков 35 мучились. Пока окончательно не доказали, что как бы мелко не нарезать окружность на равные кусочки, из таких кусочков составить ровно длину диаметра нельзя... Во сколько раз окружность больше диаметра установили. Примерно. В 3,1415926... раз.

Это и есть число "Пи". После запятой - бесконечное число цифр без всякого порядка... Такие числа называются иррациональными. Это, кстати, и означает, что из равных кусочков окружности диаметр ровно не сложить. Никогда.

Для практического применения принято запоминать всего две цифры после запятой. Запоминаем: π=3,14

Для общего образования добавлю, что число "Пи" встречается в самых различных разделах математики, а особенно в теории вероятности, это число возникает постоянно!

Но вернёмся к градусам. Вы сообразили, почему в Древнем Вавилоне круг разбили на 360 равных частей? А не на 100, к примеру? У древних вавилонян не спросишь... Для строительства, или, скажем, астрономии, круг удобно делить на равные части. А теперь прикиньте, на какие числа делится нацело 100, и на какие - 360? И в каком варианте этих делителей нацело - больше? Людям такое деление очень удобно. Но...

Как выяснилось много позже Древнего Вавилона, не всем нравятся градусы. Высшей математике они не нравятся... Высшая математика - дама серьёзная, по законам природы устроена. И эта дама заявляет: "Вы сегодня на 360 частей круг разбили, завтра на 100 разобьёте, послезавтра на 245... И что мне делать? Нет уж..." Пришлось послушаться. Природу не обманешь...

Пришлось ввести меру угла, не зависящую от человеческих придумок. Знакомьтесь - радиан!

Осмысление

Изучение нового материала.

Задачи: обеспечить восприятие, осмысление и первичное запоминание изучаемого материала, осознание своих способов проработки учебной информации

Наравне с  градусной мерой угла используется  радианная.

Возьмем на координатной плоскости окружность с центром в точке О и радиусом R. Отметим на ней дугу РМ, длина которой равна R и угол РОМ.

Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 радиан.

Градусная мера угла в 1 радиан равна:

Так как дуга длиной πR (полуокружность), стягивает центральный угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е.

И наоборот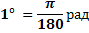

Так как π = 3,14, то 1 рад = 57,3°

Если угол содержит a радиан, то его градусная мера равна

И наоборот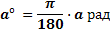

Обычно при обозначении меры угла в радианах наименование «рад» опускают.

Например, 360° = 2π рад, пишут 360° = 2π

В таблице указаны наиболее часто встречающиеся углы в градусной и радианной мере.

Закрепления новых знаний и умений.

Задачи: обеспечить повышение уровня осмысления учащимися изученного материала, глубины его усвоения

Пример 1.

Найти радианную меру угла равного а) 40° ,  б)120° ,  в)105°

Решение

а) 40° = 40·π / 180 = 2π/9

б) 120° = 120·π/180 = 2π/3

в) 105° = 105·π/180 = 7π/12

Пример 2.

Найти градусную меру угла выраженного в радианах а) π/6 ,  б) π/9,  в) 2·π/3

Решение

а) π/6 = 180°/6 = 30°

б) π/9 = 180°/9 = 20°

в) 2π/3 = 2·180°/6 = 120°

Проверка новых знаний

Задачи: установить правильность и осознанность учащимися изученного материала, выявить пробелы первичного осмысления

Работа с учебником. № 347, 348, 351

Коррекция знаний.

Задачи: скорректировать выявленные проблемы

Организация деятельности учащихся по коррекции выявленных недостатков

Индивидуальное задание.

Повторное разъяснение учителя.

Подведение итогов. Рефлексия.

Задачи: инициировать рефлексию учащихся по поводу своего эмоционального состояния, дать оценку работе отдельных учащихся и всего класса

Мобилизация учащихся на рефлексию. Оцените свою работу на уроке

Я доволен собой, у меня все получилось.

У меня не все получилось, нужно повторить.

Многое не получилось, нужно повторить.

.Выставление оценок.