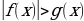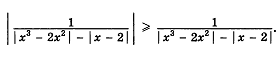Индивидуальная образовательная траектория

Индивидуальная образовательная траектория

«Если педагогика хочет воспитывать человека

во всех отношениях,

то она должна, прежде всего,

узнать его тоже во всех отношениях».

К.Д. Ушинский

Одним из приоритетных направлений

обновления современного образования

является индивидуальная траектория образования

и развития личности обучающегося, воспитанника

(выдержка из ФГОС).

Анализ психолого-педагогической литературы показывает, что понятие «индивидуальная образовательная траектория» имеет широкое значение и характеризуется несколькими направлениями реализации образовательной траектории:

– содержательное (реализуемое через образовательные программы),

– деятельностное (реализуемое через педагогические технологии),

– процессуальное (определяющее организационный аспект, виды общения).

Индивидуальная траектория – это проявление стиля учебной деятельности каждого учащегося, зависящее от его мотивации, обучаемости и осуществляемое в сотрудничестве с педагогом. Они связывают понятие «индивидуальная образовательная траектория» с понятием «образовательная программа», позволяющим обучающимся овладеть определенным уровнем образованности, отмечают способность учеников осознанно выбирать индивидуальную траекторию обучения с реализацией разнообразных вариантов развивающего обучения: личностно-ориентированного, проектно-созидательного, модульного обучения, гуманистической школы.

Индивидуальная образовательная траектория как образовательная программа рассматривается с двух сторон:

– как организационно-управленческое знание, позволяющее реализовать принцип личностной ориентации образовательного процесса через определение условий, способствующих достижению обучающимися с разными образовательными потребностями и возможностями установленного стандарта образования;

– как индивидуальную образовательную траекторию обучающегося, созданную с учетом его индивидуальных особенностей. Определение образовательной программы как индивидуальной образовательной траектории является ее ведущей характеристикой и позволяет представить образовательную программу своеобразной моделью путей достижения образовательного стандарта, когда выбор пути реализации стандарта зависит от индивидуальных особенностей конкретного учащегося.

Можно сказать, что индивидуальная образовательная траектория, индивидуальный образовательный маршрут – составляющая часть обобщенного образовательного маршрута, который, как множество индивидуальных, объединяет их в концентрированном виде.

Такой подход позволяет рассматривать понятие «индивидуальный образовательный маршрут» с двух точек зрения:

– как один из множества возможных вариантов индивидуального образовательного продвижения личности;

– как результат взаимодействия обучающегося с образовательной средой, отражающей общее, специфическое обобщенного образовательного маршрута.

Индивидуальные образовательные траектории можно трактовать как определенную последовательность элементов учебной деятельности каждого учащегося по реализации собственных образовательных целей, соответствующую их способностям, возможностям, мотивации, интересам, осуществляемую при координирующей, организующей, консультирующей деятельности педагога во взаимодействии с родителями.

Для того, чтобы определить индивидуальную траекторию развития ученика, учитель должен задавать себе вопросы:

 в чем конкретно будет состоять развитие личности школьника на основе учебной деятельности;

 какие движущие силы будут определять качественные изменения в учебной успешности;

 в какой период изменения могут проходить более интенсивно у каждого конкретного ученика;

 под влиянием каких социально-психолого-педагогических факторов возникают общие и индивидуальные прогрессивные тенденции в развитии учебной успешности личности ученика.

Сущность инновационного обучения - непрерывная коррекция личностно-ориентированной траектории обучения ученика с ожиданием обязательного успеха от обучаемых с любыми способностями. Она позволяет на каждого школьника посмотреть как на личность с особыми потенциальными возможностями.

Предполагаем, что общение с учащимися на такой основе усилит желание у них работать над собой, самоустраняя недостатки в обучении, развитии, воспитании.

В личностно-ориентированном обучении принципиальным является следующее положение: любой ученик способен найти, создать или предложить свой вариант решения любой задачи, относящейся к собственному обучению. Ученик сможет продвигаться по индивидуальной траектории изучения математики в том случае, если ему будут предоставлены следующие возможности:

• определять индивидуальный смысл изучения математики;

• ставить собственные цели в изучении конкретной темы или раздела;

• выбирать оптимальные формы и темпы обучения;

• применять те способы учения, которые наиболее соответствуют его индивидуальным особенностям;

• рефлексивно осознавать полученные результаты,

• осуществлять оценку и корректировку своей деятельности.

Это в теории.

Обучение должно быть индивидуальным. Это идеал. Как осуществить такое обучение на практике в массовой школе?

Сложно говорить об индивидуальном изучении математики вообще- в условиях ФГОС, при классно-урочной системе обучения, обязательных ОГЭ и ЕГЭ. Хотя, я считаю, углублённое изучение математики и в этом плане расширяет возможности и учителя, и обучающихся.

Что же мы делаем в этом направлении?

Очевидно, что не каждый ребенок с раннего возраста понимает, что он учится, прежде всего, для себя, для своих дальнейших достижений. Поэтому цель взрослых (родителей, педагогов и психологов) помочь им в осознании этой цели.

В работе с обучающимися в среднем и старшем звене нашей школы, учитывая различные типы мотивации к изучению математики, можно выделить следующие этапы:

• I Работа с обучающимися 5-7 классов: основное направление - комплексное формирование мотивации к изучению предмета. Диагностика потенциальных возможностей обучающихся.

• II Работа с обучающимися 8-9 классов: основное направление – осуществление педагогической поддержки ребят с выраженным интересом к изучению предметов математики, физики, и информатики + развитие мотивационной сферы обучающихся с частично сформированным стимулом к учению ( внешними мотивами).

• III Работа с обучающимися 10-11 классов: основное направление – целенаправленное развитие мотивированных обучающихся, обладающих способностями к точным наукам + педагогическое сопровождение старшеклассников с чётко сформированным внешним мотивом к учению ( подготовка к ЕГЭ).

В идеале, приоритет должен отдаваться не столько изучению готовых знаний по математике, сколько занятиям самой математикой, её проблемами. В результате образовательная деятельность ученика носит продуктивный личностный характер, а усвоение общеобразовательных стандартов происходит через сопоставление с собственными знаниями.

Основные элементы индивидуальной образовательной деятельностиученика – это

1. смысл деятельности (зачем я это делаю);

2. постановка личной цели (предвосхищающий результат);

3. план деятельности;

4. реализация плана;

5. рефлексия (осознание собственной деятельности);

6. оценка;

7. корректировка или переопределение целей.

Я предлагаю рассмотреть эти элементы или этапы на примере мониторинга за учениками 9Вкласса с углублённым изучением математики.

1. Сентябрь. Ребятам был предложен один вопрос « Почему я учусь в классе с углублённым изучением математики?», пять вариантов ответов. Можно было выбрать два варианта. Как видите, мотивы самые разные. И ребята далеко не все математически одарённые.

• Нравится заниматься математикой

• Хорошие оценки по математике, учитель говорит, что у меня есть способности.

• Так решили родители.

• Хочу после школы поступить в вуз с профильной математикой.

• За компанию с друзьями, чтобы остаться в своём классе, не уходить из школы.

1. Вопрос(сентябрь): «Какова твоя цель в изучении математики в 9 классе?»

2 варианта ответа

• Научиться решать более сложные и интересные задачи, которые не умел решать раньше.

• Подойти к изучению серьёзнее, чем в 8 классе («Начну учиться!»)

• Сдать ОГЭ.

• Сдать ОГЭ на оценку выше «3».

• Набрать около 30 баллов за экзамен, участвовать в олимпиадах и конкурсах.

1. Вопрос (сентябрь): «Как ты собираешься реализовать свою цель?»

3 варианта ответа

• На уроке не буду отвлекаться НИКОГДА.

• Начну выполнять д.з. к каждому уроку и полностью.

• Буду заниматься с репетитором.

• Не буду пропускать занятий спецкурса.

• Буду посещать занятия физ-мат школы в СмолГУ

• Буду решать задачи дополнительно, участвовать в конкурсах и олимпиадах.

1. Реализация плана(январь).

• Оценки в четвертях соответствуют моим планам

• Полноценно занимаюсь на спецкурсах

• Участвую в олимпиадах и конкурсах.

• Занимаюсь с репетитором.

• Посещаю физ-мат школу в СмолГУ

1. Вопрос (март): «Насколько успешно ты изучаешь математику в 9 классе?»

1 вариант ответа

• Я работаю изо всех сил, доволен результатом.

• Я работаю изо всех сил, но не всегда получается.

• Стараюсь через раз, но всё неплохо получается.

• Не очень стараюсь, мог бы лучше.

• Делаю всё по минимуму, лишь бы не «двойка».

1. Оценка результатов.

Как ты думаешь, какая будет твоя оценка на ОГЭ( сколько баллов наберёшь?)

Это, конечно, ещё не результат, но у нас ещё есть время на подготовку к настоящему экзамену.

1. Корректировка или переопределение целей.

Это, скорее, вопрос будущего. Кто-то из этих ребят, как и планировал, пойдёт в 10 класс с углублённым изучением математики(хотя не все из них соберутся в вуз с профильной математикой), кто-то уйдёт в другое учебное заведение, в класс с другим профилем. В большой мере это будет зависеть от результатов сдачи экзамена, от ощущения себя на экзамене.

Это был пример достаточно долгосрочного движения ученика по индивидуальной образовательной траектории – в течение 9-го класса.

Параллельно мне хотелось бы рассмотреть более локальное использованиеэлементов личностно-ориентированного обучения на уроках математики – например, при изучении отдельной темы на одном или нескольких уроках.

Вспомним, что при конструировании индивидуальных траекторий образовательной деятельности обучающихся усвоение знаний и способов деятельности может происходить на трех уровнях:

– на уровне осознанного восприятия и запоминания, которое внешне проявляется в точном и близком к оригиналу воспроизведении учебного материала;

– на уровне применения знаний и способов деятельности по образцу или в сходной ситуации;

– на уровне творческого применения знания и способов деятельности.

Опять вернёмся к 9 В классу. Алгебра. Тема – «Решение неравенств с модулем».

Как мы уже заметили, ученики в классе самые разные – сильные и слабые, не все успешно изучают математику на повышенном уровне. Заметим также, что в общеобразовательном 9 классе такой отдельной темы нет. Неравенства с модулем решаются ознакомительно, самые элементарные. В заданиях ОГЭ модуль встречается тоже на уровне определения. В учебнике углубления большое количество заданий этой темы позиционируются, как задания повышенной сложности. Таким образом, далеко не все ученики готовы на высоком уровне разобраться со сложными неравенствами этого вида.

Как разработать уроки, чтобы ученики могли одновременно продвигаться по своим индивидуальным образовательным траекториям в общей для всех образовательной области? Какова основная цель учителя по отношению к индивидуальной самореализации учеников во время уроков?

Будем работать по вышеозначенному плану. Рассмотрим основные этапы деятельности с точки зрения индивидуальной образовательной траектории.

1. Предполагаемые цели учеников. Способы их постановки учениками. (Примечание для учителя: представьте, какие цели смогут поставить себе ученики, выполняя ваши задания, и запишите их).

• Научиться решать элементарные неравенства вида , ,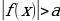

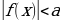• Научиться ещёрешатьнеравенства вида ,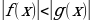

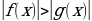
• Научиться решатьнеравенства вида ,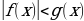

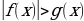
• Научиться решатьнеравенства, содержащие несколько модулей.

• Научиться решать нестандартные неравенства, содержащие модули, в том числе, с использованием свойств функций и метода введения новой переменной.

1. Главная проблема изучения темы (записывается одна или несколько проблем).

• Научиться классифицировать неравенства с модулем.

• Научиться использовать для решения оба подхода к определению модуля – аналитический и графический (с помощью числовой прямой).

1. Фундаментальный образовательный объект, в направлении которого планируется деятельность учеников.

• Решение неравенств.

Этап диагностики ученических целей можно провести с помощью анкетирования или фронтального опроса. Каждому ученику предлагается список целей, в котором он отмечает самые главные для него. Например:

1) изучить материал учебника;

2) усвоить основные алгоритмы;

3) подготовить исследование по одной из проблем неравенств с модулем;

4) хорошо подготовиться к зачету (контрольной работе, экзамену);

5) выполнить самостоятельное исследование по выбранной теме;

6) овладеть методами изучения и объяснения изучаемых в теме явлений;

7) углублённо рассмотреть конкретные вопросы темы;

8) научиться решать прикладные неравенства, в том числе, на уроках физики;

9) проявить и развить свои способности (перечислить);

10) организовать свою учебу по теме: поставить достижимые цели, составить реальный план, выполнить его и оценить свои результаты;

11) научиться аргументированно отстаивать свою точку зрения в ходе изучения темы;

12) получить хорошую отметку на контрольной работе;

13) научиться решать задачи и проблемы по теме;

14) свой вариант цели.

Анализ ответов подобной анкеты позволяет учителю судить об образовательном настрое учащихся, мотивах их учебы, индивидуальных склонностях, например, выбор целей 1, 4, 12 свидетельствует о формальной ориентации ученика в обучения; 2, 7, 13 - о наличии когнитивных (познавательных) мотивов; 3, 5, 8 – о креативных наклонностях; 6, 9, 10, 14 – о методологических приоритетах деятельности.

После анализа полученных от учеников данных учитель формулирует приоритетные цели обучения, которые группируются по выбранным направлениям.

1. Реализация плана.Как именно на уроках предполагается достичь индивидуальной самореализации учеников. (Что нужно для этого предусмотреть?)

• Различные цели обучающихсяв изучении материала.

• Различные уровни усвоения предыдущих тем – решение линейных, квадратных, рациональных неравенств.

• Различные темпы работы.

• Умение обучающихся работать по алгоритму.

• Творческий подход к решению каждого задания.

• Отношение обучающегося к скрупулёзнойвычислительной деятельности.

1. Этапы и виды деятельности учеников на уроках по мере изучения темы.

• Повторение двух подходов к определению модуля.

• Повторение понятия равносильности неравенств.

• Повторение понятий системы и совокупности неравенств.

• Работа с учебником, изучение примеров

• Создание конспектов, опорных схем- шпаргалок, выработка алгоритмов решения.

• Практикумы по решению неравенств различных типов.

Примерная схема- шпаргалка для решения неравенств с модулем.

С её использованием в рамках данных уроков решение неравенств происходит быстрее.

Но не все неравенства сразу поддаются классификации.

1. Формулировки заданий ученикам на каждом уроке. Задания задаются таким образом, чтобы допускались разные варианты их выполнения, например:

• Распределите неравенства по группам.

• Перепишите неравенство в удобном для решения виде.

• Составьте план решения неравенства.

Например, рассмотрим неравенство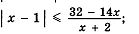

• На что в первую очередь обращаем внимание? ( Модуль - с одной стороны, знак – меньше)

• С чего удобно начать рассуждение.

• Начинаем всегда с определения модуля.

• Неравенство равносильно системе.

1. Предполагаемые результаты выполнения заданий учениками (не менее двух - трёх типов результатов).

• Умение подобрать пример решения в тетради или в учебнике.

• Умение классифицировать тип неравенства с модулем.

• Умение составить план решения, исходя из определения модуля и с помощью творческого подхода.

• Умение довести до конца процесс решения и получение ответа.

1. Задание ученикам по рефлексии их деятельности.

• Понимаю ли я, что обсуждается на каждом этапе урока?

• Могу ли я выполнить вышеперечисленные задания (что может мне помочь: учебник, тетрадь с классной работой)?

• Могу ли полностью выполнить домашнее задание самостоятельно?

• Могу ли я объяснить товарищу метод решения данного неравенства

• Готов ли я к самостоятельной проверочной работе по данной теме

• Какое неравенство я могу решить?

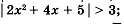
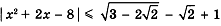
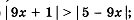
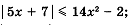
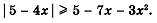
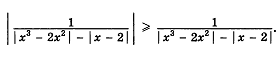
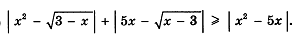
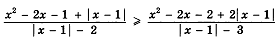
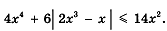
1. Задания на дом (разные варианты на выбор или индивидуально).

1. Формы контроля и оценки результатов уроков.

• Проверка домашнего задания.

• Фронтальный опрос.

• Проверка классной работы в процессе урока.

• Ответ у доски с комментариями.

• Самостоятельные работы – обучающие - на каждом уроке и проверочная – на последнем.

Каждый контроль преследует конкретную цель - анализ результатов контроля. Оценки по письменным работам комментируются. Обязательно отмечаю успешные работы, задачи, решённые оригинально.

• Обучающийся должен быть уверен в объективности оценочных суждений, для этого требования к выполнению задания, критерии оценок сообщаются заранее.

• Объясняю систему экзаменационных баллов ОГЭ и ЕГЭ, часто использую эту систему для оценки письменных работ.

• Использую взаимоконтроль, например, при выполнении маленьких тестов по теории.

• Использую самооценку и самоконтроль.

• Стараюсь, чтобы преобладала функция обучающая над контролирующей. При выполнении самостоятельных работ я всегда консультирую по выполнению заданий.

• Оцениваю результаты деятельности (а не личность обучающегося).

• Использую поощрения - обязательно отмечаю тех обучающихся, у которых наблюдаю динамику в развитии.

Для реализации индивидуального маршрута обучающихся на уроках математики я использую несколько видов вида траекторий:

• для учеников с опережающими темпами развития (это моя опора).

• для учеников с ослабленным здоровьем(хотя в углублении математики таким детям очень сложно);

• для учеников с низким уровнем учебной мотивации и трудностями в обучении;

• для одаренных учащихся.

Условная дифференциация учащихся на эти группы нужна лишь для того, чтобы выбрать оптимальные формы и методы взаимодействия в ходе учебной деятельности.

Самостоятельная работа по данной теме предусмотрена трёх уровней – задания из учебника по различным типам неравенств с модулем.

Результаты работы: «5» - 2, «4» - 5, «3» - 7, «2» - 4

Заметим, что это оценки повышенного уровня изучения математики. С простейшими базовыми неравенствами справились все.

Возможность индивидуальной траектории образования ученика предполагает, что ученик при изучении темы может, например, выбрать один из следующих подходов:

• образное или логическое познание,

• углубленное или энциклопедическое изучение,

• ознакомительное, выборочное или расширенное усвоение темы.

Сохранение логики предмета, его структуры и содержательных основ будет достигаться с помощью фиксированного объема фундаментальных образовательных объектов и связанных с ними проблем, которые наряду с индивидуальной траекторией обучения обеспечат достижение учениками нормативного образовательного уровня.

Условием достижения целей и задач индивидуальной траектории образования является сохранение индивидуальных особенностей учеников, развитие их уникальности и неповторимости. Для этого применяю элементы различных технологий:

• разноуровневое обучение -  индивидуальные задания различной степени сложности:

• уровень А (базовый),

• уровень Б (средний уровень сложности),

• уровень В (повышенный уровень сложности),

• уровень С (олимпиадный).

• командное обучение - организация парной и групповой работы (взаимопроверка тестов, математических диктантов, групповое решение проблемной задачи).

• создание ситуации успеха - формулирую детям задания, которые предполагают их выполнение индивидуально каждым учеником.

Например: придумайте неравенство с модулем, которое можете решить или выберите его из учебника.

• создание ситуации выбора - предлагаю ученикам выбрать тему творческой работы.

• игровая технология проведения устного счета «Кто быстрее и без ошибок?» (считаем устно, записываем в тетрадях ответ).

• урок – лекция с применением компьютерных презентаций.

Таким образом, технологии применения личностно ориентированного подхода  на уроках математики формируют потребность умственного труда.

Попробуем подвести итоги рассуждений.

Образование несет в себе определенное внутреннее противоречие, вызванное коллективными по формам способами получения и индивидуальными по результатам последствиями. Таким образом, личность в процессе получения оказывается в сложной ситуации необходимости определения своих позиций, своих целевых установок, своих конечных точек, к которым она стремится. Процесс непростой, его сложность вызывается, прежде всего, отсутствием у обучающегося опыта или небольшим по объему опытом деятельности. Практически ученику трудно решить эту проблему в условиях развития вообще самостоятельно; необходима продуманная и своеобразная организация, необходимо целенаправленное управление данным процессом.

Траектория-след от движения. Программа – ее план. На мой взгляд, принцип индивидуальной образовательной траектории невозможно полностью реализовать в рамках традиционных форм (классно-урочной системы). Но какие-то элементы мы можем использовать и в нашей повседневной работе. Необходимо выводить за рамки этой системы одаренных учеников, предлагать индивидуальный раздаточный материал, что поможет дать разноуровневое объяснение материала и разнотипные задания для каждого ученика.

Таким образом, при составлении индивидуальной образовательной траектории:

• учитель создает ученику возможность для выбора, выступая, как консультант и советчик. На уроке учитель учитывает индивидуальные интересы школьников; особенности учебной деятельности; предпочитаемые виды учебных занятий; способы работы с учебным материалом; особенности усвоения учебного материала; виды учебной деятельности;

• для ученика при составлении индивидуальной траектории самое важное – оценить свои возможности, способности, перспективы, интересы, усилия, которые он предполагает приложить для изучения того или иного материала либо чтобы добиться запланированного результата.

Результаты движения по образовательной траектории можно проверять, ориентируясь на созданный учениками продукт; полученные знания, которые реализуются в умениях оперировать ими в стандартной или творческой ситуации, отмечая формирование различного вида умений – мыслительных, коммуникативных, познавательных и т.д. Кроме того, необходима постоянная обратная связь, позволяющая не только корректировать движение ученика по траекториям (а иногда и саму траекторию), но и оценивать его продвижение.

В заключение, заметим, что диапазон возможностей, предоставляемых ученику в его движении по индивидуальной образовательной траектории, достаточно широк: от индивидуализированного познания фундаментальных образовательных объектов и личностной трактовки изучаемых понятий до построения индивидуальной картины мира и личного образа жизни.

Несомненно, ничего принципиально нового я вам, скорее всего, не сообщила. Но я постаралась ещё раз порассуждать и свести воедино все те формы и методы, которые все мы используем и применяем на наших уроках. Несмотря на постоянно меняющиеся стандарты образования, вернее, в соответствии с ними, главная цель нашей деятельности –это научить школьников учиться.

Цель обучения ребенка состоит в том, чтобы сделать его

способнымразвиваться дальше без помощи учителя. Хаббард Э

13
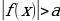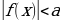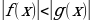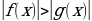
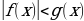