Интегрированный урок по алгебре и началам анализа и физике. Решение задач по теме «Гармонические колебания»

« Весь наш предшествующий опыт приводит к убеждению, что природа является осуществлением того, что математически проще всего представить»

А. Эйнштейн

«Что можно сделать хорошего, особенно в физике, если не сводить все к мере и степени?»

А.Вольта

Интегрированный урок по алгебре и началам анализа и физике

ГБОУ ЛНР « Родаковская ООШ I – III ступеней

11 класс

Учителя : Дьяченко Л.И.

Григорьева Е.Н.

Решение задач по теме « Гармонические колебания »

Цели урока:

• образовательная : проверить усвоение физических формул и умений брать первую и вторую производную от тригонометрических функций, формировать умения решать расчетные и качественные задачи, анализировать графики и физические закономерности
• развивающая : развивать творческое мышление, развивать умение применять знания в новой нестандартной ситуации, развивать умение анализировать, делать выводы
• воспитательная : воспитывать доброжелательное отношение друг к другу, взаимопонимание и взаимопомощь

Задачи урока

• выявить связи, существующие между физикой и математикой;

• показать, что на основе производной возможен анализ конкретных физических ситуаций

Устная работа

Построить график функции

y= 3 sin(2x+  /3)–2

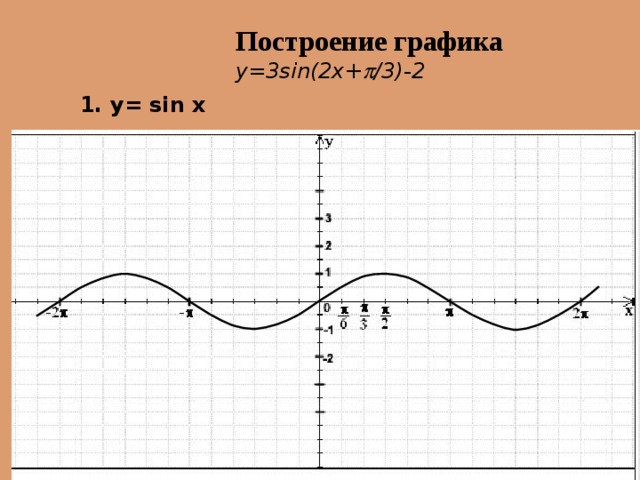
Построение графика y=3sin(2x+  /3) – 2

1. y= sin x

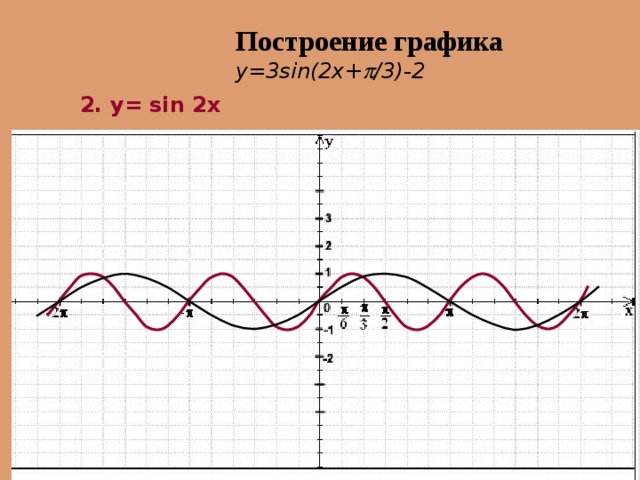
Построение графика y=3sin(2x+  /3) – 2

2. y= sin 2x

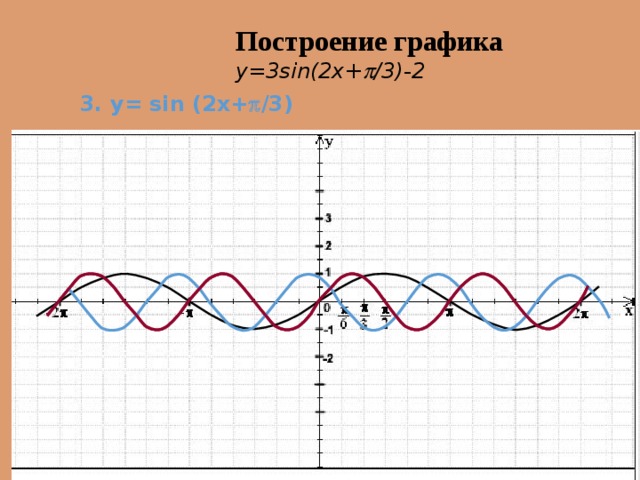
Построение графика y=3sin(2x+  /3) – 2

3. y= sin (2x+  /3)

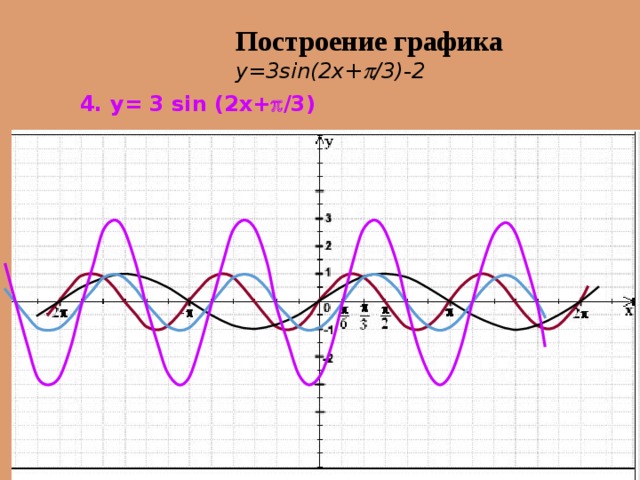
Построение графика y=3sin(2x+  /3) – 2

4. y= 3 sin (2x+  /3)

Построение графика y=3sin(2x+  /3) – 2

5. y= 3 sin (2x+  /3) – 2

Преобразование графиков

y = Asin(kx–n)+m

  Функция

1

Преобразование

2

    y=sin(kx)

  y=sin(x–m)

Сжатие вдоль оси OX относительно оси OY в k раз

3

Параллельный перенос вдоль оси OX на m единиц

    y=А sin x

4

  y=sin x+n

5

Растяжение вдоль оси OY относительно оси OX в А раз

    y= – sin x

6

Параллельный перенос вдоль оси OY на n единиц

    y= sin (–x)

Симметричное отражение относительно оси OX

Симметричное отражение относительно оси OY

Найти амплитуду, циклическую частоту и период колебаний если координата тела меняется по закону x = - 0,5 cos 4π t .

Номер ответа

X m , м

1

-0,5

2

ω о , рад/с

3

4π

-0,5

Т, с

0,5

0,5

4π

4

5

0,5

4

2

4

4π

• Варианты ответов: 1) υ x (t)= x m ω o sinω o t
• 2) υ x (t)= x m sinω o t
• 3) υ x (t)= -x m ω o sinω o t
• 4) υ x (t)= 1/ω o x m ω o sinω o t

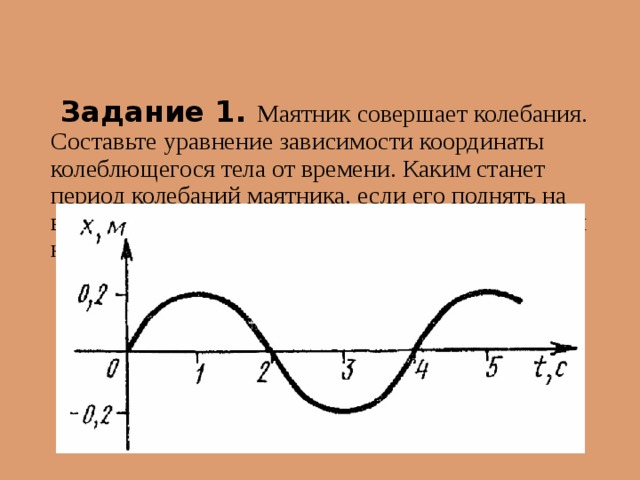
Задание 1. Маятник совершает колебания. Составьте уравнение зависимости координаты колеблющегося тела от времени. Каким станет период колебаний маятника, если его поднять на высоту равную радиусу Земли, если его перенести на Луну? Найдите длину нити маятника.

Жан Бернар Леон Фуко 18.09.1819-11.02.1868

Французский физик и астроном Леон Фуко, впервые осуществил свой эксперимент в 2 часа ночи 8 января 1851 года в погребе своего дома на углу улиц Асса́ и Вожира́р в Париже. Для этого был использован маятник длиной 2 метра. В феврале с разрешения Доминика Франсуа Араго он повторил опыт в Парижской обсерватории, на этот раз удлинив маятник до 11 метров.

Первая публичная демонстрация была осуществлена уже в марте 1851года в парижском  Пантеоне: под куполом Пантеона он подвесил металлический шар массой 28 кг с закреплённым на нём остриём на стальной проволоке длиной 67 м.

Крепление маятника позволяло ему свободно колебаться во всех направлениях, под точкой крепления было сделано круговое ограждение диаметром 6 м, по краю ограждения была насыпана песчаная дорожка таким образом, чтобы маятник в своём движении мог при её пересечении прочерчивать на песке отметки. Чтобы избежать бокового толчка при пуске маятника, его отвели в сторону и привязали верёвкой, после чего верёвку пережгли

Задание 2

Колебательное движение точки описывается уравнением х=0,05cos20πt . Записать уравнения зависимости скорости и ускорения от времени. Найти наибольшие значения скорости и ускорения. В каких положениях достигаются эти значения? Найти координату, проекцию скорости и ускорения спустя 1/60 с после начала движения.

В Исаакиевском соборе в Ленинграде маятник Фуко был запущен в ночь с 11 на 12 апреля 1931 года и снят в 1986 году, сейчас хранится в подвалах собора. Длина нити этого маятника — 98 м.

В Донецком национальном техническом университете 17.04.2018 года состоялось уникальное событие – впервые в Донбассе был запущен маятник Фуко

Это интересно Биение сердца - пример вынужденных колебаний

В течение минуты сердце выбрасывает в аорту около 4 л крови. Сердце человека в среднем сокращается 100 тысяч раз в сутки. За 70 лет жизни оно сокращается 2 миллиарда 600 миллионов раз и перекачивает при этом 250 миллионов литров крови. (информация на экране) Изучение вынужденных электромагнитных колебаний мы начнем на следующем уроке.

Задание 3

Груз массой 1 кг, подвешенный к пружине с жесткостью 100 Н/м, совершает колебания с амплитудой 10 см. Написать уравнение зависимости координаты от времени. Написать формулу, выражающую зависимость силы упругости от времени. Найти наибольшее значение силы упругости и значение силы упругости через 1/6 периода.

«Все сведения о природных телах и их свойствах должны содержать точные указания на число, вес, объем, размеры… Практика рождается только из тесного соединения физики и математики»

Френсис Бекон