| № | Задание | Решение | Ответ |
| 1 | Даны два квадрата, диагонали которых равны 10 и 6. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов. |
|
|
| 2 | Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции. |
|
|
| 3 | Точки O(0, 0), A(10, 8), B(8, 2), C(2, 6) являются вершинами четырехугольника. Найдите абсциссу точки P пересечения его диагоналей. |
|
|
| 4 | Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 
|
|
|
| 5 | На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 51. Найдите площадь заштрихованной фигуры. 
|
|
|
| 6 | В треугольнике ABC угол C равен  , ,  , ,  . Найдите . Найдите  . . |
|
|
| 7 | В треугольнике ABC угол C равен  , CH — высота, , CH — высота,  , ,  . Найдите BH. . Найдите BH. |
|
|
| 8 | Один из внешних углов треугольника равен  . Углы, не смежные с данным внешним углом, относятся как . Углы, не смежные с данным внешним углом, относятся как  . Найдите наибольший из них. Ответ дайте в градусах. . Найдите наибольший из них. Ответ дайте в градусах. |
|
|
| 9 | Найдите хорду, на которую опирается угол  , вписанный в окружность радиуса 3. , вписанный в окружность радиуса 3. |
|
|
| 10 | Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону. |
|
|
| 11 | Найдите квадрат расстояния между вершинами  и и  прямоугольного параллелепипеда, для которого прямоугольного параллелепипеда, для которого  , ,  , ,  . . |
|
|
| 12 | В правильной шестиугольной призме  все ребра равны 21. Найдите расстояние между точками все ребра равны 21. Найдите расстояние между точками  и и  . . |
|
|
| 13 | Найдите расстояние между вершинами  и и  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. 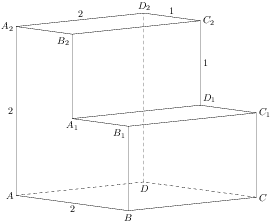
|
|
|
| 14 | В правильной треугольной пирамиде   — середина ребра — середина ребра  , ,  — вершина. Известно, что — вершина. Известно, что  , а площадь боковой поверхности равна 96 . Найдите длину отрезка , а площадь боковой поверхности равна 96 . Найдите длину отрезка  . . |
|
|
| 15 | | Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Радиус сферы равен  . Найдите образующую конуса. . Найдите образующую конуса. |
|
|
|
| 16 | Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 6. Найдите объем параллелепипеда. |
|
|
| 17 | Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 18. |
|
|
| 18 | Объем прямоугольного параллелепипеда равен 72. Одно из его ребер равно 4. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру. |
|
|
| 19 | Найдите объем правильной шестиугольной призмы, стороны основания которой равны 6, а боковые ребра равны  . . |
|
|
| 20 | Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны  и наклонены к плоскости основания под углом 30 и наклонены к плоскости основания под углом 30 . . |
|
|
| 21 | В прямоугольном параллелепипеде известны ребра: АВ=35, АD=12,СС1=21.Найдите угол между плоскостями АВС и А1 DB |
|
|
| 22 | В параллелограмме АВСD биссектрисы углов при стороне АD делят сторону ВС точками M и N так что ВM:МN=3:5. Найти ВС, еслиАВ=12 |
|
|
| № | Задание | Решение | Ответ |
| 1 | Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность? |
|
|
| 2 | Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45 . . |
|
|
| 3 | Точки O(0, 0), A(10, 8), B(8, 2), C(2, 6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей. |
|
|
| 4 | Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 
|
|
|
| 5 | На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 1. Найдите площадь заштрихованной фигуры. |
|
|
| 6 | В треугольнике ABC угол C равен  , ,  , ,  . Найдите . Найдите  . . |
|
|
| 7 | В треугольнике ABC угол C равен  , CH — высота, , CH — высота,  , ,  . Найдите AH. . Найдите AH. |
|
|
| 8 | Один из углов равнобедренного треугольника равен  . Найдите один из других его углов. Ответ дайте в градусах. . Найдите один из других его углов. Ответ дайте в градусах. |
|
|
| 9 | Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах. |
|
|
| 10 | В ромбе  угол угол  равен равен  . Найдите угол . Найдите угол  . Ответ дайте в градусах. . Ответ дайте в градусах. |
|
|
| 11 | Найдите расстояние между вершинами  и и  прямоугольного параллелепипеда, для которого прямоугольного параллелепипеда, для которого  , ,  , ,  . . |
|
|
| 12 | В правильной шестиугольной призме  все ребра равны 35. Найдите расстояние между точками все ребра равны 35. Найдите расстояние между точками  и и  . . |
|
|
| 13 | Найдите расстояние между вершинами  и и  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. 
|
|
|
| 14 | В правильной треугольной пирамиде   — середина ребра — середина ребра  , ,  — вершина. Известно, что — вершина. Известно, что  , а площадь боковой поверхности равна 54 . Найдите длину отрезка , а площадь боковой поверхности равна 54 . Найдите длину отрезка  . . |
|
|
| 15 | Шар вписан в цилиндр. Площадь поверхности шара равна 30. Найдите площадь полной поверхности цилиндра. |
|
|
| 16 | Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 80. Найдите высоту цилиндра. |
|
|
| 17 | Объем конуса равен 168. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса. |
|
|
| 18 | | Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 6 и 5. Объем параллелепипеда равен 90. Найдите третье ребро параллелепипеда, выходящее из той же вершины. |
|
|
|
| 19 | В цилиндрический сосуд, в котором находится 10 литров воды, опущена деталь. При этом уровень жидкости в сосуде поднялся в 1,9 раза. Чему равен объем детали? Ответ выразите в литрах. |
|
|
| 20 | В правильной четырехугольной пирамиде высота равна 3, боковое ребро равно 10. Найдите ее объем. |
|
|
| 21 | В прямоугольном параллелепипеде известны ребра: АВ=35, АD=12,СС1=21.Найдите угол между плоскостями АВС и А1 DB |
|
|
| 22 | В параллелограмме АВСD биссектрисы углов при стороне АD делят сторону ВС точками M и N так что ВM:МN=3:5. Найти ВС, еслиАВ=12 |
|
|
| № | Задание | Решение | Ответ |
| 1 | Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах. |
|
|
| 2 | Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах. |
|
|
| 3 | Точки  (0, 0), (0, 0),  (6, 8), (6, 8),  (8, 2) являются вершинами треугольника. Найдите длину его средней линии (8, 2) являются вершинами треугольника. Найдите длину его средней линии  , параллельной , параллельной  . . |
|
|
| 4 | Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 
|
|
|
| 5 | На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 9. Найдите площадь заштрихованной фигуры. |
|
|
| 6 | В треугольнике ABC угол C равен  , ,  , ,  . Найдите . Найдите  . . |
|
|
| 7 | В треугольнике ABC угол C равен  , ,  . Найдите синус внешнего угла при вершине A. . Найдите синус внешнего угла при вершине A. |
|
|
| 8 | Сумма двух углов треугольника и внешнего угла к третьему равна  . Найдите этот третий угол. Ответ дайте в градусах. . Найдите этот третий угол. Ответ дайте в градусах. |
|
|
| 9 | Радиус окружности равен 1. Найдите величину острого вписанного угла, опирающегося на хорду, равную  . Ответ дайте в градусах. . Ответ дайте в градусах. |
|
|
| 10 | В ромбе  угол угол  равен равен  . Найдите угол . Найдите угол  . Ответ дайте в градусах. . Ответ дайте в градусах. |
|
|
| 11 | Найдите расстояние между вершинами  и и  прямоугольного параллелепипеда, для которого прямоугольного параллелепипеда, для которого  , ,  , ,  . . |
|
|
| 12 | В правильной шестиугольной призме  все ребра равны 19. Найдите расстояние между точками все ребра равны 19. Найдите расстояние между точками  и и  . . |
|
|
| 13 | Найдите расстояние между вершинами  и и  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. |
|
|
| 14 | В правильной треугольной пирамиде   — середина ребра — середина ребра  , ,  — вершина. Известно, что — вершина. Известно, что  , а площадь боковой поверхности равна 54 . Найдите длину отрезка , а площадь боковой поверхности равна 54 . Найдите длину отрезка  . . |
|
|
| 15 | Площадь боковой поверхности цилиндра равна  , а высота — 7 . Найдите диаметр основания. , а высота — 7 . Найдите диаметр основания. |
|
|
| 16 | Прямоугольный параллелепипед описан около сферы радиуса 7,5. Найдите его объем. |
|
|
| 17 | Объем первого цилиндра равен 22 м3. У второго цилиндра высота в 3 раза больше, а радиус основания — в 2 раза меньше, чем у первого. Найдите объем второго цилиндра. Ответ дайте в кубических метрах. |
|
|
| 18 | | Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 12 и 18. Найдите ребро равновеликого ему куба. |
|
|
|
| 19 | Найдите объем V конуса, образующая которого равна 51 и наклонена к плоскости основания под углом 30 . В ответе укажите . В ответе укажите  . . |
|
|
| 20 | Объем правильной четырехугольной пирамиды SABCD равен 132. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC. |
|
|
| 21 | В прямоугольном параллелепипеде известны ребра: АВ=35, АD=12,СС1=21.Найдите угол между плоскостями АВС и А1 DB |
|
|
| 22 | В параллелограмме АВСD биссектрисы углов при стороне АD делят сторону ВС точками M и N так что ВM:МN=3:5. Найти ВС, еслиАВ=12 |
|
|
| № | Задание | Решение | Ответ |
| 1 | Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма. |
|
|
| 2 | Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции. |
|
|
| 3 | Точки O(0, 0), A(10, 0), B(8, 6), C(2, 6) являются вершинами трапеции. Найдите длину ее средней линии DE |
|
|
| 4 | Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 
|
|
|
| 5 | На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 2. Найдите площадь заштрихованной фигуры. |
|
|
| 6 | В треугольнике ABC угол C равен  , ,  , ,  . Найдите . Найдите  . . |
|
|
| 7 | В тупоугольном треугольнике ABC  , высота AH равна 24, , высота AH равна 24,  . Найдите . Найдите  |
|
|
| 8 | Углы треугольника относятся как  . Найдите меньший из них. Ответ дайте в градусах. . Найдите меньший из них. Ответ дайте в градусах. |
|
|
| 9 | Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную  . Ответ дайте в градусах. . Ответ дайте в градусах. |
|
|
| 10 | Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как  . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 48. . Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 48. |
|
|
| 11 | Найдите угол  прямоугольного параллелепипеда, для которого прямоугольного параллелепипеда, для которого  , ,  , ,  . Ответ дайте в градусах. . Ответ дайте в градусах. |
|
|
| 12 | В правильной шестиугольной призме  все ребра равны все ребра равны  . Найдите расстояние между точками . Найдите расстояние между точками  и и  . . |
|
|
| 13 | Найдите расстояние между вершинами  и и  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. |
|
|
| 14 | В правильной треугольной пирамиде   — середина ребра — середина ребра  , ,  — вершина. Известно, что — вершина. Известно, что  , а площадь боковой поверхности равна 84 . Найдите длину отрезка , а площадь боковой поверхности равна 84 . Найдите длину отрезка  . . |
|
|
| 15 | Диаметр основания конуса равен 152, а длина образующей — 95 . Найдите высоту конуса. |
|
|
| 16 | В цилиндрический сосуд налили  воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 2 см. Чему равен объем детали? Ответ выразите в воды. Уровень жидкости оказался равным 12 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 2 см. Чему равен объем детали? Ответ выразите в  . . |
|
|
| 17 | Объем куба равен 125. Найдите площадь его поверхности. |
|
|
| 18 | Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 6, боковое ребро равно 5. Найдите объем призмы. |
|
|
| 19 | Во сколько раз увеличится объем конуса, если его радиус основания увеличить в 14 раз? |
|
|
| 20 | Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой. |
|
|
| 21 | В прямоугольном параллелепипеде известны ребра: АВ=35, АD=12,СС1=21.Найдите угол между плоскостями АВС и А1 DB |
|
|
| 22 | В параллелограмме АВСD биссектрисы углов при стороне АD делят сторону ВС точками M и N так что ВM:МN=3:5. Найти ВС, еслиАВ=12 |
|
|
| № | Задание | Решение | Ответ |
| 1 | Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма. |
|
|
| 2 | Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции. |
|
|
| 3 | Найдите абсциссу точки пересечения прямой, заданной уравнением  , с осью Ox. , с осью Ox. |
|
|
| 4 | Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 
|
|
|
| 5 | На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 2. Найдите площадь заштрихованной фигуры. |
|
|
| 6 | В треугольнике ABC угол C равен  , ,  , ,  . Найдите . Найдите  . . |
|
|
| 7 | В треугольнике ABC  , высота AH равна 24, , высота AH равна 24,  . Найдите . Найдите  . . |
|
|
| 8 | Один острый угол прямоугольного треугольника в 4 раза больше другого. Найдите больший острый угол. Ответ дайте в градусах. |
|
|
| 9 | Найдите хорду, на которую опирается угол  , вписанный в окружность радиуса , вписанный в окружность радиуса  . . |
|
|
| 10 | К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 8, 23, 78. Найдите периметр данного треугольника. |
|
|
| 11 | Найдите угол  прямоугольного параллелепипеда, для которого прямоугольного параллелепипеда, для которого  , ,  , ,  . Ответ дайте в градусах. . Ответ дайте в градусах. |
|
|
| 12 | В правильной шестиугольной призме  все ребра равны все ребра равны  . Найдите расстояние между точками . Найдите расстояние между точками  и и  . . |
|
|
| 13 | Найдите расстояние между вершинами  и и  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. |
|
|
| 14 | В правильной треугольной пирамиде  медианы основания пересекаются в точке медианы основания пересекаются в точке  . Площадь треугольника . Площадь треугольника  равна 30, объем пирамиды равен 210 . Найдите длину отрезка равна 30, объем пирамиды равен 210 . Найдите длину отрезка  . . |
|
|
| 15 | Высота конуса равна 57, а длина образующей — 95 . Найдите диаметр основания конуса. |
|
|
| 16 | В цилиндрическом сосуде уровень жидкости достигает 48 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй цилиндрический сосуд, диаметр которого в 4 раза больше диаметра первого? Ответ выразите в сантиметрах. |
|
|
| 17 | Объем параллелепипеда  равен 9. Найдите объем треугольной пирамиды равен 9. Найдите объем треугольной пирамиды  . . |
|
|
| 18 | Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды. |
|
|
| 19 | Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём конуса, если объём цилиндра равен 159. |
|
|
| 20 | Радиусы трех шаров равны 6, 8 и 10. Найдите радиус шара, объем которого равен сумме их объемов. |
|
|
| 21 | В прямоугольном параллелепипеде известны ребра: АВ=35, АD=12,СС1=21.Найдите угол между плоскостями АВС и А1 DB |
|
|
| 22 | В параллелограмме АВСD биссектрисы углов при стороне АD делят сторону ВС точками M и N так что ВM:МN=3:5. Найти ВС, еслиАВ=12 |
|
|
| № | Задание | Решение | Ответ |
| 1 | Найдите площадь ромба, если его высота равна 2, а острый угол 30 . . |
|
|
| 2 | Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150 . Найдите площадь трапеции. . Найдите площадь трапеции. |
|
|
| 3 | Найдите ординату точки пересечения прямых, заданных уравнениями  и и  . . |
|
|
| 4 | Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 1 см (см. рис.). Ответ дайте в квадратных сантиметрах. 
|
|
|
| 5 | На клетчатой бумаге нарисовано два круга. Площадь внутреннего круга равна 2. Найдите площадь заштрихованной фигуры. |
|
|
| 6 | В треугольнике ABC угол C равен  , ,  , ,  . Найдите . Найдите  . . |
|
|
| 7 | | В тупоугольном треугольнике ABC  , высота AH равна 4. Найдите , высота AH равна 4. Найдите  . . |
|
|
|
| 8 | В треугольнике ABC угол C равен  , CH — высота, угол A равен , CH — высота, угол A равен  . Найдите угол BCH. Ответ дайте в градусах. . Найдите угол BCH. Ответ дайте в градусах. |
|
|
| 9 | Центральный угол на  больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах. больше острого вписанного угла, опирающегося на ту же дугу окружности. Найдите вписанный угол. Ответ дайте в градусах. |
|
|
| 10 | Около окружности, радиус которой равен  , описан квадрат. Найдите радиус окружности, описанной около этого квадрата. , описан квадрат. Найдите радиус окружности, описанной около этого квадрата. |
|
|
| 11 | Найдите угол  прямоугольного параллелепипеда, для которого прямоугольного параллелепипеда, для которого  , ,  , ,  . Ответ дайте в градусах. . Ответ дайте в градусах. |
|
|
| 12 | В правильной шестиугольной призме  все ребра равны 26. Найдите угол все ребра равны 26. Найдите угол  . Ответ дайте в градусах. . Ответ дайте в градусах. |
|
|
| 13 | Найдите расстояние между вершинами  и и  многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.
|
|
|
| 14 | В правильной треугольной пирамиде  медианы основания пересекаются в точке медианы основания пересекаются в точке  . Площадь треугольника . Площадь треугольника  равна 13, объем пирамиды равен 78 . Найдите длину отрезка равна 13, объем пирамиды равен 78 . Найдите длину отрезка  |
|
|
| 15 | Высота конуса равна 25, а диаметр основания — 120. Найдите образующую конуса. |
|
|
| 16 | В основании прямой призмы лежит квадрат со стороной 7. Боковые ребра равны  . Найдите объем цилиндра, описанного около этой призмы. . Найдите объем цилиндра, описанного около этой призмы. |
|
|
| 17 | Площадь грани прямоугольного параллелепипеда равна 21. Ребро, перпендикулярное этой грани, равно 3. Найдите объем параллелепипеда. |
|
|
| 18 | | Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 12, а объем равен  . . |
|
|
|
| 19 | Диагональ куба равна  . Найдите его объем. . Найдите его объем. |
|
|
| 20 | Диаметр основания конуса равен 6, а угол при вершине осевого сечения равен 90°. Вычислите объем конуса, деленный на  . . |
|
|
| 21 | В прямоугольном параллелепипеде известны ребра: АВ=35, АD=12,СС1=21.Найдите угол между плоскостями АВС и А1 DB |
|
|
| 22 | В параллелограмме АВСD биссектрисы углов при стороне АD делят сторону ВС точками M и N так что ВM:МN=3:5. Найти ВС, еслиАВ=12 |
|
|




















