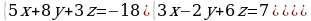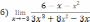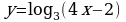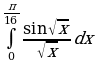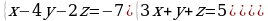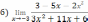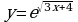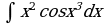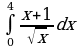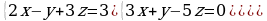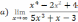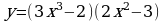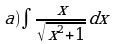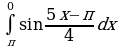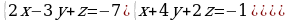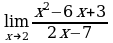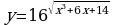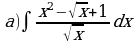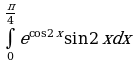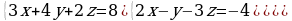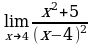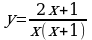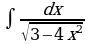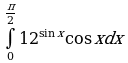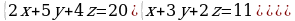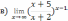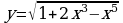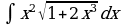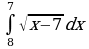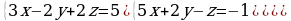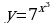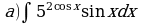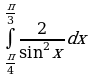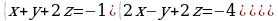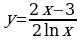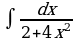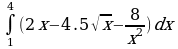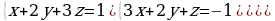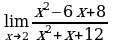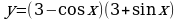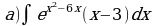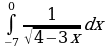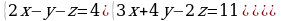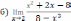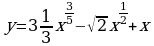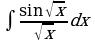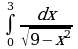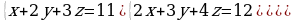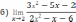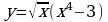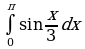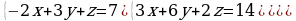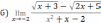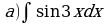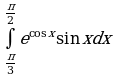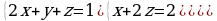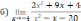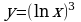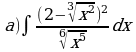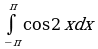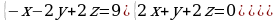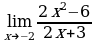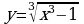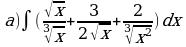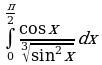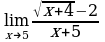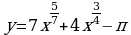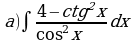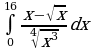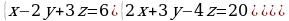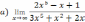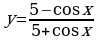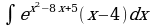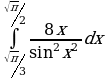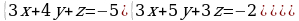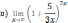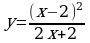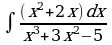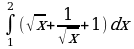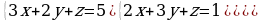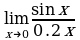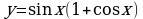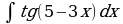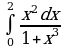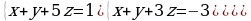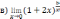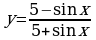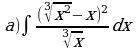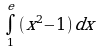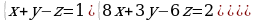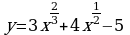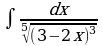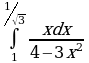Управление образования и науки липецкой области
Государственное областное бюджетное профессиональное образовательное учреждение
«Липецкий машиностроительный колледж»
| Комплект Контрольно – измерительных материалов |
| общепрофессиональной дисциплины
|
| ЕН.01 Математика 
(код и наименование МДК)
|
|
основной профессиональной образовательной программы
|
| по специальности:
10.02.04 Обеспечение информационной безопасности телекоммуникационных систем |

(код и наименование специальности)
Липецк 2021
Комплект контрольно-измерительных материалов по учебной дисциплине ЕН.01 Математика разработан на основе Федерального государственного образовательного стандарта (далее ФГОС СПО) по специальности
10.02.04 Обеспечение информационной безопасности телекоммуникационных систем
Организация разработчик: ГОБПОУ «Липецкий машиностроительный колледж»
Разработчик:
Дымова Галина Ивановна, преподаватель цикла естественнонаучных дисциплин
ГОБПОУ «Липецкий машиностроительный колледж»
|
|
|
|
|
| ОДОБРЕНО: | УТВЕРЖДАЮ: |
| на заседании МО ЦК ЕНД ______________ Г,И. Дымова Протокол № _________ «_____» _____________ 2021г. | Зам. директора по УР _________________ Ю.А. Гуськова «_____» __________________ 2021г. |
СОДЕРЖАНИЕ
| I Паспорт комплекта контрольно-измерительных материалов |
|
| 1 Область применения |
|
| 2 Объекты оценивания – результаты освоения УД |
|
| 3 Формы контроля и оценки результатов освоения УД |
|
| 4 Система оценивания комплекта КИМ текущего контроля и |
|
| промежуточной аттестации |
|
|
|
|
| II Текущий контроль и оценка результатов обучения |
|
| Спецификация письменной контрольной работы |
|
|
III Промежуточная аттестация по УД |
|
| Спецификация дифференциального зачёта |
|
Паспорт комплекта контрольно-измерительных материалов
1.Область применения
Комплект контрольно - измерительных материалов (КИМ) предназначен для проверки результатов освоения учебной дисциплины ЕН.01 «Математика», образовательной программы среднего профессионального образования по специальности СПО
10.02.04 Обеспечение информационной безопасности телекоммуникационных систем
2. Объекты оценивания – результаты освоения МДК
КИМ позволяет оценить следующие результаты освоения ЕН.01 «Математика» в соответствии с ФГОС специальности СПО 10.02.04 Обеспечение информационной безопасности телекоммуникационных систем
В результате изучения обязательной части учебного цикла обучающийся должен:
уметь:
выполнять операции над матрицами и решать системы линейных уравнений;
выполнять операции над множествами;
применять методы дифференциального и интегрального исчисления;
использовать основные положения теории вероятностей и математической статистики;
применять стандартные методы и модели к решению типовых вероятностных и статистических задач;
пользоваться пакетами прикладных программ для решения вероятностных и статистических задач;
планировать свое профессиональное развитее
информационные технологии для поиска и решения профессионально значимых задач
знать:
основы линейной алгебры и аналитической геометрии;
-основные положения теории множеств;
-основные понятия и методы дифференциального и интегрального исчисления;
-основные понятия и методы теории вероятностей и математической статистики;
-основные статистические пакеты прикладных программ;
-логические операции, законы и функции алгебры, логики
методы самоконтроля в решении профессиональных задач
способы и методы сбора, анализа и систематизации данных посредством информационных технологий
3. Формы контроля и оценки результатов освоения
Контроль и оценка результатов освоения – это выявление, измерение и оценивание знаний, умений и формирующихся общих и профессиональных компетенций в рамках освоения УД.
В соответствии с учебным планом специальности 10.02.04 Обеспечение информационной безопасности телекоммуникационных систем, рабочей программой ЕН.01 Математика предусматривается текущий и промежуточный контроль.
3.1 Формы текущего контроля
Текущий контроль успеваемости представляет собой проверку усвоения учебного материала, регулярно осуществляемую на протяжении семестра.
Текущий контроль результатов освоения ЕН.01 в соответствии с рабочей программой и календарно- тематическим планом происходит при использовании следующих форм контроля:
- выполнение и защита практических работ,
- проверка выполнения контрольных работ.
Во время проведения учебных занятий дополнительно используются следующие формы текущего контроля – устный опрос, решение задач, тестирование по темам отдельных занятий.
Выполнение и защита практических работ. Практические работы проводятся с целью усвоения и закрепления практических умений и знаний. В ходе практической работы студенты приобретают умения предусмотренные рабочей программой ЕН.01, учатся использовать формулы, и применять различные методики расчета, анализировать полученные результаты и делать выводы, опираясь на теоретические знания.
Список практических работ:
Практическое занятие №1. Действия с матрицами. Определители 2-го,3-го порядков. Нахождение обратной матрицы, ранга матрицы.
Практическое занятие №2. Решение СЛУ по формулам Крамера, методом Гаусса.
Практическое занятие №3. Операции над векторами. Вычисление модуля и скалярного произведения. Уравнение линии на плоскости. Уравнение прямой и окружности.
Практическое занятие №4. Вычисление пределов функции в точке. Вычисление пределов функции на бесконечности. Раскрытие неопределенностей. Правило Лапиталя. Вычисление пределов с помощью правила Лапиталя.
Практическая работа №5. Исследование функции с помощью производной и построение графика
Практическое занятие №6. Метод замены переменной в неопределенном интеграле. Интегрирование по частям. Универсальная подстановка. Применение математических методов интегрального исчисления для решения профессиональных задач.
Практическое занятие №7. Вычисление простейших определенных интегралов. Вычисление определенных интегралов с помощью замены переменных, интегрирования по частям. Решение прикладных задач: вычисление площадей, объемов.
Практическое занятие №8 . Исследование сходимости знакоположительных рядов. Исследование сходимости знакочередующихся рядов.
Практическое занятие №9. Линейные однородные и неоднородные ДУ первого порядка.
Практическое занятие №10. Решение задач на классическое определение вероятностей, вычисление вероятностей с использованием теоремы сложения и умножения вероятностей.
Практическое занятие №11. Обработка и нахождение статистических оценок научных и практических данных.
Проверка выполнения самостоятельной работы.
Самостоятельная работа направлена на закрепление студентами практических умений и знаний при подготовке к промежуточной аттестации
Самостоятельная подготовка студентов по ЕН.01 предполагает следующие виды и формы работы:
- Систематическая проработка конспектов занятий, учебной и специальной литературы.
- Выполнение расчетно-вычислительных заданий.
- Работа со справочной литературой.
- Подготовка дифференцированному зачету;
Задания на выполнение самостоятельной работы представлены в методических рекомендациях по организации и проведению самостоятельной работы студентов.
Проверка выполнения контрольных работ.
Контрольная работа проводится с целью контроля усвоенных умений и знаний и последующего анализа типичных ошибок и затруднений студентов в конце изучения темы или раздела. Согласно календарно-тематическому плану ЕН.01 предусмотрено проведение контрольной работы в конце курса изучения учебной дисциплины.
Вопросы для устного опроса, примеры задач по темам отдельных занятий представлены в методических рекомендациях по организации и проведению самостоятельной работы студентов.
3.2. Форма промежуточной аттестации
Промежуточная аттестация по ЕН.01. Математика – дифференцированный зачёт, спецификация которого содержится в данном КИМ.
Студенты допускаются к сдаче зачёта при выполнени, практических и контрольных работ, предусмотренных рабочей программой и календарно-тематическим планом ЕН.01. Математика.
4. Система оценивания КИМ текущего контроля и промежуточной аттестации
При оценивании практической и самостоятельной работы студента учитывается следующее:
качество выполнения практической работы;
качество оформления отчета по практической работе;
качество письменных и устных ответов.
Каждый вид работы оценивается по 5-ти бальной шкале.
«5» (отлично) – за глубокое и полное овладение содержанием учебного материала, в котором студент свободно и уверенно ориентируется; за умение практически применять теоретические знания, высказывать и обосновывать свои суждения. Оценка «5» (отлично) предполагает грамотное и логичное изложение ответа.
«4» (хорошо) – если студент полно освоил учебный материал, владеет научно-понятийным аппаратом, ориентируется в изученном материале, осознанно применяет теоретические знания на практике, грамотно излагает ответ, но содержание и форма ответа имеют отдельные неточности.
«3» (удовлетворительно) – если студент обнаруживает знание и понимание основных положений учебного материала, но излагает его неполно, непоследовательно, допускает неточности, в применении теоретических знаний при ответе на практико-ориентированные вопросы; не умеет доказательно обосновать собственные суждения.
«2» (неудовлетворительно) – если студент имеет разрозненные, бессистемные знания, допускает ошибки в определении базовых понятий, искажает их смысл; не может практически применять теоретические знания.
II . Текущий контроль и оценка результатов обучения
Спецификация обязательной контрольной работы по ЕН.01 Математика
1. Назначение письменной контрольной работы – оценить уровень подготовки студентов ЕН.01 Математика с целью проверки знаний и умений по разделам учебной дисциплины
2. Содержание письменной контрольной работы определяется в соответствии с рабочей программой ЕН.01 Математика с целью проверки знаний и умений по разделам.
3. Принципы отбора содержания письменной контрольной работы:
ориентация на требования к результатам освоения разделов представленным в рабочей программе ЕН.01 Математика:
уметь:
выполнять операции над матрицами и решать системы линейных уравнений;
выполнять операции над множествами;
применять методы дифференциального и интегрального исчисления;
использовать основные положения теории вероятностей и математической статистики;
применять стандартные методы и модели к решению типовых вероятностных и статистических задач;
пользоваться пакетами прикладных программ для решения вероятностных и статистических задач;
планировать свое профессиональное развитее
информационные технологии для поиска и решения профессионально значимых задач
знать:
основы линейной алгебры и аналитической геометрии;
-основные положения теории множеств;
-основные понятия и методы дифференциального и интегрального исчисления;
-основные понятия и методы теории вероятностей и математической статистики;
-основные статистические пакеты прикладных программ;
-логические операции, законы и функции алгебры, логики
методы самоконтроля в решении профессиональных задач
способы и методы сбора, анализа и систематизации данных посредством информационных технологий
4. Структура письменной контрольной работы
4.1. Письменная контрольная работа включает 30 вариантов заданий, каждый из которых состоит из 7 заданий.
4.2. Задания письменной контрольной работы предлагаются в традиционной форме.
4.3. Варианты письменной контрольной работы равноценны по трудности, одинаковы по структуре, параллельны по расположению заданий: под одним и тем же порядковым номером во всех вариантах письменной проверочной работы находится задание, проверяющее один и тот же элемент содержания.
5. Система оценивания письменной контрольной работы
5.1. Каждое задание контрольной работы в традиционной форме оценивается по 5-тибалльной шкале:
«5» (отлично) – за глубокое и полное овладение содержанием учебного материала, в котором студент свободно и уверенно ориентируется; научно-понятийным аппаратом; за умение практически применять теоретические знания, качественно выполнять все виды практических работ. Оценка «5» (отлично) предполагает грамотное и логичное изложение ответа (в устной или письменной форме) на практико-ориентированные вопросы; обоснование собственного высказывания с точки зрения известных теоретических положений.
«4» (хорошо) – если студент полно освоил учебный материал, владеет научно-понятийным аппаратом, ориентируется в изученном материале, осознанно применяет теоретические знания на практике, грамотно излагает ответ (в устной или письменной форме), но содержание и форма ответа имеют отдельные неточности.
«3» (удовлетворительно) – если студент обнаруживает знание и понимание основных положений учебного материала, но излагает его неполно, непоследовательно, допускает неточности в определении понятий, в применении теоретических знаний при ответе на практико-ориентированные вопросы; не умеет доказательно обосновать собственные суждения.
«2» (неудовлетворительно) – если студент имеет разрозненные, бессистемные знания по междисциплинарным курсам, допускает ошибки в определении базовых понятий, искажает их смысл; не может практически применять теоретические знания.
5.2 Итоговая оценка определяется как средний балл по всем заданиям (вопросам).
6. Время выполнения письменной контрольной работы
На выполнение письменной контрольной работы отводится 90 минут.
7. Рекомендации по подготовке к обязательной контрольной работе
При подготовке к контрольной работе рекомендуется использовать учебники, имеющие гриф Министерства образования РФ.
Основные и дополнительные источники:
Богомолов Н.В., Самойленко П.И. «Математика» учебник для средних спец. учебных заведений -5 изд., переработанное и доп. – М.: издательство Юрайт, 2017.
Григорьев С.Г., Иволгина С.В. «Математика»: учебник для студ. образоват. учреждений сред.проф. образования под редакцией В.А. Гусева. – 11-е изд., стер. – М.: Издательский центр «Академия», 2017.
Богомолов Н.В. практические занятия по математике: учебное пособие для СПО / Н.В. Богомолов. – 12-е изд., перераб. И доп. –М.: издательство Юрайт, 2018.
Башмаков М.И. Математика. Задачник: учебное пособие для студ. Учреждений сред.проф. образования / М.И. Башмаков. – 6-е изд., стер. – М.: Издательский центр «Академия», 2017г.
Интернет-ресурсы:
Методическая копилка учителя математики [Электронный ресурс]: база данных содержит методические и информационные средства для учащихся и педагогов среднего звена общего полного и начального профессионального образования – Электрон.дан. – Режим доступа: http://metod-kopilka.ru – Загл. с экрана;
Федеральное хранилище Единой коллекции цифровых образовательных ресурсов [Электронный ресурс] / Национальный фонд подготовки кадров – Электрон.дан. – Режим доступа: http://school-collection.edu.ru/catalog/– Загл. с экрана;
Открытый класс. Сетевые образовательные сообщества [Электронный ресурс]: / Национальный фонд подготовки кадров – Электрон.дан. – Режим доступа: http://www.openclass.ru/ – Загл. с экрана;
Сеть творческих учителей [Электронный ресурс]: информация и материалы по использованию информационных и коммуникационных технологий (ИКТ) в образовании – Электрон.дан. – Режим доступа: http://it-n.ru/– Загл. с экрана;
Единое окно доступа к образовательным ресурсам [Электронный ресурс]: каталог образовательных Интернет - ресурсов/ ФГУ ГНИИ ИТТ «Информика». – Электрон.дан. – Режим доступа: http://window.edu.ru/– Загл. с экрана;
Инструкция для студентов
1 Форма проведения текущего контроля знаний по разделам учебной дисциплины:
Элементы линейной алгебры
Элементы аналитической геометрии
Математический анализ
Основы теории вероятности и математической статистики
Контрольная работа в традиционной форме.
2 Принципы отбора содержания обязательной контрольной работы:
Ориентация на требования к результатам освоения разделов:
Элементы линейной алгебры
Элементы аналитической геометрии
Математический анализ
Основы теории вероятности и математической статистики
Представленным в рабочей программе учебной дисциплине «Математика»:
уметь:
выполнять операции над матрицами и решать системы линейных уравнений;
выполнять операции над множествами;
применять методы дифференциального и интегрального исчисления;
использовать основные положения теории вероятностей и математической статистики;
применять стандартные методы и модели к решению типовых вероятностных и статистических задач;
пользоваться пакетами прикладных программ для решения вероятностных и статистических задач;
планировать свое профессиональное развитее
информационные технологии для поиска и решения профессионально значимых задач
знать:
основы линейной алгебры и аналитической геометрии;
-основные положения теории множеств;
-основные понятия и методы дифференциального и интегрального исчисления;
-основные понятия и методы теории вероятностей и математической статистики;
-основные статистические пакеты прикладных программ;
-логические операции, законы и функции алгебры, логики
методы самоконтроля в решении профессиональных задач
способы и методы сбора, анализа и систематизации данных посредством информационных технологий
3 Структура обязательной контрольной работы:
3.1 Обязательная контрольная работа состоит из 7 заданий.
3.2 Задания обязательной контрольной работы предлагаются в традиционной форме.
4 Система оценивания обязательной контрольной работы:
4.1 Задания оцениваются по 5-ти бальной шкале следующим образом:
Оценка «5» (отлично) выставляется за правильное выполнение 7-6 заданий.
Оценка «4» (хорошо) выставляется за правильное выполнение 5 задания.
Оценка «3» (удовлетворительно) выставляется за правильное выполнение 4 заданий.
Оценка «2» (неудовлетворительно) выставляется за неправильное выполнение 3 и более заданий.
5 Время выполнения обязательной контрольной работы:
На выполнение обязательной контрольной работы отводится 90 минут.
Чтобы успешно справиться с заданиями контрольной работы, нужно внимательно прочитать вопросы. Именно внимательное, вдумчивое чтение – половина успеха.
Выполняйте задания в том порядке, в котором они даны. Для экономии времени пропускайте задание, которое не удается выполнить сразу, и переходите к следующему. Если после выполнения всей работы у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
КОНТРОЛЬНАЯ РАБОТА
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 1 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 2
|
Решите систему уравнений методом Крамера: 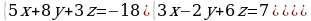 Вычислите предел функции: 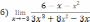
Найдите производную функции: 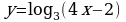 Найдите неопределенный интеграл: 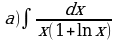 Вычислите определенный интеграл: 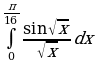
Решите дифференциальной уравнение: у”+3y’=0
В партии из 12 деталей имеется 4 нестандартных. Берут 3 детали наудачу. Найти закон распределения дискретной случайной величины равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию
| Решите систему уравнений методом Крамера: 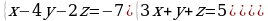 Вычислите предел функции: 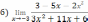
Найдите производную функции: 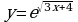
Найдите неопределенный интеграл: 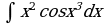
Вычислите определенный интеграл: 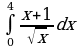
Решите дифференциальной уравнение: exdx=y2dy В партии из 12 деталей имеется 4 нестандартных. Берут 3 детали наудачу. Найти закон распределения дискретной случайной величины равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
|
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 3 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 4
|
Решите систему уравнений методом Крамера: 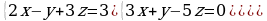 Вычислите предел функции: 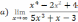
Найдите производную функции: 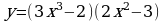
Найдите неопределенный интеграл: 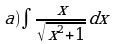
Вычислите определенный интеграл: 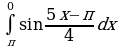
Решите дифференциальной уравнение: y”-5y’+6y=0
В партии из 12 деталей имеется 4 нестандартных. Берут 3 детали наудачу. Найти закон распределения дискретной случайной величины равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
| 1. Решите систему уравнений методом Крамера: 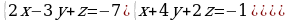 Вычислите предел функции: 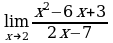
Найдите производную функции: 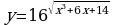
Найдите неопределенный интеграл: 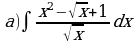
Вычислите определенный интеграл: 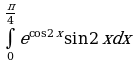
Решите дифференциальной уравнение: y”+y’+y=0 В партии из 13 деталей имеется 9 нестандартных. Берут 3 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию
|
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 5 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 6
|
Решите систему уравнений методом Крамера: 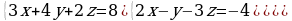 Вычислите предел функции: 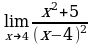
Найдите производную функции: 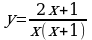
Найдите неопределенный интеграл: 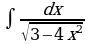
Вычислите определенный интеграл: 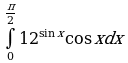
Решите дифференциальной уравнение: 2y3dy=3dx
В партии из 10 деталей имеется 7 стандартных. Берут 2 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
| Решите систему уравнений методом Крамера: 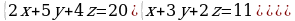 Вычислите предел функции: 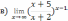
Найдите производную функции: 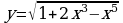
Найдите неопределенный интеграл: 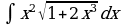
Вычислите определенный интеграл: 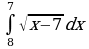
Решите дифференциальной уравнение: y”-8y’=0
В коробке 10 карандашей, из них 5 карандашей поломанных. Из этой коробки берут наугад 3 карандаша. Найти закон распределения дискретной случайной величины X, равной числу поломанных карандашей. Найти математическое ожидание, дисперсию
|
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 7 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 8
|
Решите систему уравнений методом Крамера: 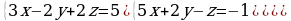 Вычислите предел функции: 
Найдите производную функции: 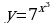
Найдите неопределенный интеграл: 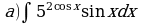
Вычислите определенный интеграл: 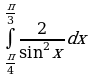
Решите дифференциальной уравнение: y”+20y’+19y=0
В партии из 12 деталей имеется 4 нестандартных. Берут 3 детали наудачу. Найти закон распределения дискретной случайной величины равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
| Решите систему уравнений методом Крамера: 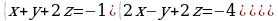 Вычислите предел функции:
Найдите производную функции: 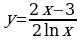
Найдите неопределенный интеграл: 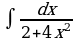
Вычислите определенный интеграл: 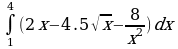
Решите дифференциальной уравнение: y”-y=0
В партии из 13 деталей имеется 9 нестандартных. Берут 3 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
|
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 9 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 10
|
Решите систему уравнений методом Крамера: 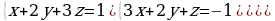 Вычислите предел функции: 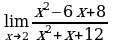
Найдите производную функции: 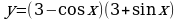
Найдите неопределенный интеграл: 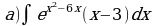
Вычислите определенный интеграл: 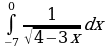
Решите дифференциальной уравнение:y”+6y’+13y=0
В партии из 10 деталей имеется 7 стандартных. Берут 2 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию. | 1. Решите систему уравнений методом Крамера: 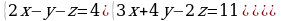 2. Вычислите предел функции: 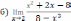
3. Найдите производную функции: 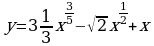
4. Найдите неопределенный интеграл: 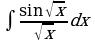
5. Вычислите определенный интеграл: 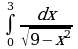
Решите дифференциальной уравнение: y”-4y’+8y=0
В коробке 10 карандашей, из них 5 карандашей поломанных. Из этой коробки берут наугад 3 карандаша. Найти закон распределения дискретной случайной величины X, равной числу поломанных карандашей. Найти математическое ожидание, дисперсию.
|
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 11 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 12
|
Решите систему уравнений методом Крамера: 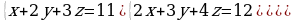 Вычислите предел функции: 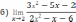
Найдите производную функции: 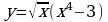
Найдите неопределенный интеграл: 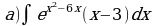
Вычислите определенный интеграл: 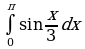
Решите дифференциальной уравнение: y”+10y’-11y=0 Задает ли закон распределения дискретной случайной величины данная таблица 1 | X | 2 | 3 | 4 | 5 | 6 | | P | 0,1 | 0,2 | 0,25 | 0,17 | 0,3 |
| 1. Решите систему уравнений методом Крамера: 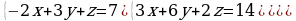 2. Вычислите предел функции: 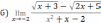
3. Найдите производную функции: 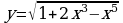
4. Найдите неопределенный интеграл: 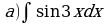
5. Вычислите определенный интеграл: 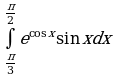
Решите дифференциальной уравнение: y”+12y’+36y=0
Задает ли закон распределения дискретной случайной величины данная таблица | X | 21 | 22 | 23 | 24 | 25 | | P | 0,11 | 0,19 | 0,2 | 0,2 | 0,3 |
|
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 13 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 14
|
Решите систему уравнений методом Крамера: 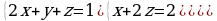 Вычислите предел функции: 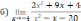
Найдите производную функции: 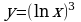
Найдите неопределенный интеграл: 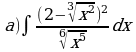
Вычислите определенный интеграл: 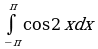
Решите дифференциальной уравнение: y”-9y=0
Задает ли закон распределения дискретной случайной величины данная таблица | X | 21 | 22 | 23 | 24 | 25 | | P | 0,11 | 0,19 | 0,2 | 0,2 | 0,3 |
| 1. Решите систему уравнений методом Крамера: 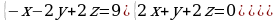 2. Вычислите предел функции: 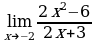
3. Найдите производную функции: 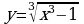
4. Найдите неопределенный интеграл: 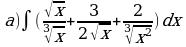
5. Вычислите определенный интеграл: 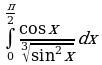
. Решите дифференциальной уравнение: y”+4y’+3y=0
Задает ли закон распределения дискретной случайной величины данная таблица | X | 21 | 22 | 23 | 24 | 25 | | P | 0,11 | 0,19 | 0,2 | 0,2 | 0,3 |
|
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 15 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 16
|
Решите систему уравнений методом Крамера: 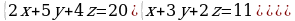 Вычислите предел функции: 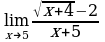
Найдите производную функции: 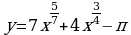
Найдите неопределенный интеграл: 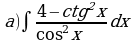
Вычислите определенный интеграл: 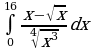
Решите дифференциальной уравнение: y”-y’-2y=0
В партии из 12 деталей имеется 4 нестандартных. Берут 3 детали наудачу. Найти закон распределения дискретной случайной величины равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
| 1. Решите систему уравнений методом Крамера: 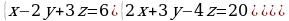 2. Вычислите предел функции: 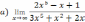
3. Найдите производную функции: 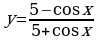
4. Найдите неопределенный интеграл: 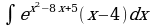
5. Вычислите определенный интеграл: 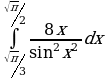
6.Решите дифференциальной уравнение: y”+2y’-8y=0
В партии из 13 деталей имеется 9 нестандартных. Берут 3 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию
|
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 17 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 18
|
Решите систему уравнений методом Крамера: 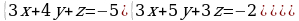 Вычислите предел функции: 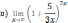
Найдите производную функции: 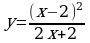
Найдите неопределенный интеграл: 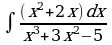
Вычислите определенный интеграл: 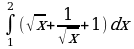
Решите дифференциальной уравнение: y”-4y’+4y=0 В партии из 13 деталей имеется 9 нестандартных. Берут 3 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию
| 1. Решите систему уравнений методом Крамера: 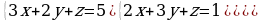 2. Вычислите предел функции: 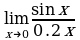
3. Найдите производную функции: 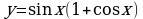
4. Найдите неопределенный интеграл: 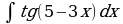
5. Вычислите определенный интеграл: 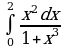
6. Решите дифференциальной уравнение: y”-6y’+9y=0
В коробке 10 карандашей, из них 5 карандашей поломанных. Из этой коробки берут наугад 3 карандаша. Найти закон распределения дискретной случайной величины X, равной числу поломанных карандашей. Найти математическое ожидание, дисперсию.
|
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 19 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 20
|
Решите систему уравнений методом Крамера: 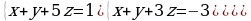 Вычислите предел функции: 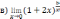
Найдите производную функции: 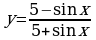
Найдите неопределенный интеграл: 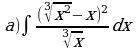
Вычислите определенный интеграл: 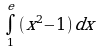
Решите дифференциальной уравнение: y”-2y’+y=0
В партии из 12 деталей имеется 4 нестандартных. Берут 3 детали наудачу. Найти закон распределения дискретной случайной величины равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию
| 1. Решите систему уравнений методом Крамера: 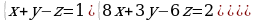 2. Вычислите предел функции: 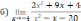
3. Найдите производную функции: 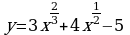
4. Найдите неопределенный интеграл: 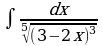
5. Вычислите определенный интеграл: 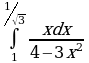
6.Решите дифференциальной уравнение: y”+3y’+2y=0
В партии из 13 деталей имеется 9 нестандартных. Берут 3 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию
|
|
|
|
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 21 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 22
|
Решите систему уравнений методом Крамера: 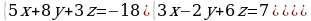 Вычислите предел функции: 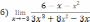
Найдите производную функции: 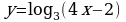 Найдите неопределенный интеграл: 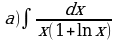 Вычислите определенный интеграл: 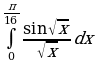
Решите дифференциальной уравнение: у”+3y’=0
В партии из 10 деталей имеется 7 стандартных. Берут 2 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию
| Решите систему уравнений методом Крамера: 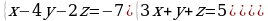 Вычислите предел функции: 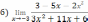
Найдите производную функции: 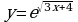
Найдите неопределенный интеграл: 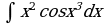
Вычислите определенный интеграл: 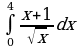
Решите дифференциальной уравнение: exdx=y2dy
В коробке 10 карандашей, из них 5 карандашей поломанных. Из этой коробки берут наугад 3 карандаша. Найти закон распределения дискретной случайной величины X, равной числу поломанных карандашей. Найти математическое ожидание, дисперсию.
|
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 23 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 24
|
Решите систему уравнений методом Крамера: 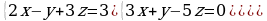 Вычислите предел функции: 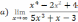
Найдите производную функции: 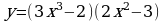
Найдите неопределенный интеграл: 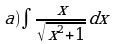
Вычислите определенный интеграл: 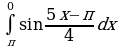
Решите дифференциальной уравнение: y”-5y’+6y=0
В коробке 10 карандашей, из них 5 карандашей поломанных. Из этой коробки берут наугад 3 карандаша. Найти закон распределения дискретной случайной величины X, равной числу поломанных карандашей. Найти математическое ожидание, дисперсию.
| Решите систему уравнений методом Крамера: 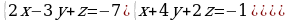 Вычислите предел функции: 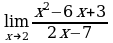
Найдите производную функции: 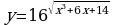
Найдите неопределенный интеграл: 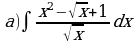
Вычислите определенный интеграл: 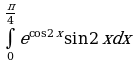
Решите дифференциальной уравнение: y”+y’+y=0
В партии из 12 деталей имеется 4 нестандартных. Берут 3 детали наудачу. Найти закон распределения дискретной случайной величины равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию
|
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 25 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 26
|
Решите систему уравнений методом Крамера: 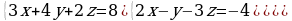 Вычислите предел функции: 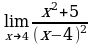
Найдите производную функции: 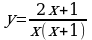
Найдите неопределенный интеграл: 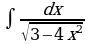
Вычислите определенный интеграл: 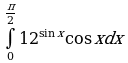
Решите дифференциальной уравнение: 2y3dy=3dx
В партии из 12 деталей имеется 4 нестандартных. Берут 3 детали наудачу. Найти закон распределения дискретной случайной величины равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
| Решите систему уравнений методом Крамера: 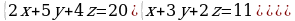 Вычислите предел функции: 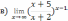
Найдите производную функции: 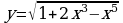
Найдите неопределенный интеграл: 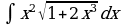
Вычислите определенный интеграл: 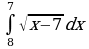
Решите дифференциальной уравнение: y”-8y’=0
В партии из 13 деталей имеется 9 нестандартных. Берут 3 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
|
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 27 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 28
|
Решите систему уравнений методом Крамера: 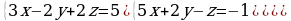 Вычислите предел функции: 
Найдите производную функции: 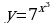
Найдите неопределенный интеграл: 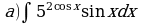
Вычислите определенный интеграл: 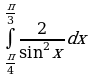
Решите дифференциальной уравнение: y”+20y’+19y=0
В партии из 13 деталей имеется 9 нестандартных. Берут 3 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
| Решите систему уравнений методом Крамера: 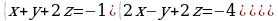 Вычислите предел функции: 
Найдите производную функции: 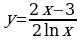
Найдите неопределенный интеграл: 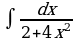
Вычислите определенный интеграл: 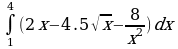
Решите дифференциальной уравнение: y”-y=0
В коробке 10 карандашей, из них 5 карандашей поломанных. Из этой коробки берут наугад 3 карандаша. Найти закон распределения дискретной случайной величины X, равной числу поломанных карандашей. Найти математическое ожидание, дисперсию.
|
| Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 29 | Семестровая контрольная работа по дисциплине: «МАТЕМАТИКА»( для студентов 2 курса) ВАРИАНТ 30
|
Решите систему уравнений методом Крамера: 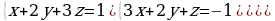 Вычислите предел функции: 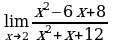
Найдите производную функции: 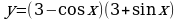
Найдите неопределенный интеграл: 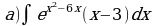
Вычислите определенный интеграл: 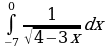
Решите дифференциальной уравнение:y”+6y’+13y=0
В партии из 12 деталей имеется 4 нестандартных. Берут 3 детали наудачу. Найти закон распределения дискретной случайной величины равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
| 1. Решите систему уравнений методом Крамера: 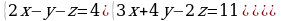 2. Вычислите предел функции: 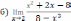
3. Найдите производную функции: 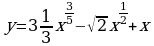
4. Найдите неопределенный интеграл: 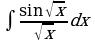
5. Вычислите определенный интеграл: 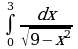
6.Решите дифференциальной уравнение: y”-4y’+8y=0
В партии из 13 деталей имеется 9 нестандартных. Берут 3 детали на удачу. Найти закон распределения дискретной случайной величины, равной числу стандартных деталей в выборке. Найти математическое ожидание, дисперсию.
|
III Промежуточная аттестация
Спецификация
дифференциального зачёта по ЕН.01 Математика
1. Назначение зачёта – оценить уровень подготовки студентов по ЕН.01 Математика с целью установления их готовности к дальнейшему усвоению ОПОП специальности
10.02.04 Обеспечение информационной безопасности телекоммуникационных систем
2. Содержание зачёта определяется в соответствии с ФГОС СПО специальности
10.02.04 Обеспечение информационной безопасности телекоммуникационных систем
и рабочей программой ЕН.01 Математика.
3. Принципы отбора содержания зачёта:
Ориентация на требования к результатам освоения ЕН.01 Математика , представленным в соответствии с ФГОС СПО специальностей 10.02.04 Обеспечение информационной безопасности телекоммуникационных систем и рабочей программой ЕН.01 Математика.
уметь:
выполнять операции над матрицами и решать системы линейных уравнений;
выполнять операции над множествами;
применять методы дифференциального и интегрального исчисления;
использовать основные положения теории вероятностей и математической статистики;
применять стандартные методы и модели к решению типовых вероятностных и статистических задач;
пользоваться пакетами прикладных программ для решения вероятностных и статистических задач;
планировать свое профессиональное развитее
информационные технологии для поиска и решения профессионально значимых задач
знать:
основы линейной алгебры и аналитической геометрии;
-основные положения теории множеств;
-основные понятия и методы дифференциального и интегрального исчисления;
-основные понятия и методы теории вероятностей и математической статистики;
-основные статистические пакеты прикладных программ;
-логические операции, законы и функции алгебры, логики
методы самоконтроля в решении профессиональных задач
способы и методы сбора, анализа и систематизации данных посредством информационных технологий
4. Структура дифференциального зачёта
4.1. Задания представлены в виде устных вопросов.
4.2. Задания предлагаются в традиционной форме.
5. Перечень разделов, тем ЕН.01 Математика включенных в дифференциальный зачёт
Элементы линей ной алгебры
Элементы аналитической геометрии
Математический анализ
Основы теории вероятности и математической статистики
6. Система оценивания вопросов
6.1. Каждое задание оценивается в 2 балл. За правильный ответ присуждается 2 балл. За неправильный ответ или его отсутствие ставиться 0-1 баллов. Оценка получается простым сложением баллов. Округление производить по правилам математики.
Критерии оценки:
оценка «5» - 6 баллов
оценка «4» - 5-4 баллов
оценка «3» - 3 балла
6.2 Итоговая оценка за зачёт определяется как средний балл по всем вопросам.
6.3 Уровень владения материалом должен быть оценен не ниже чем на 3 балла.
7. Время проведения зачёта
На выполнение задания на зачёте студенту отводится не более 30минут.
Инструкция для студентов
1 Форма проведения промежуточной аттестации по учебной дисциплине «Математика» дифференцированный зачёт в традиционной форме.
2 Принципы отбора содержания дифференцированный зачёта:
Ориентация на требования к результатам освоения ЕН.01 Математика , представленным в соответствии с ФГОС СПО 10.02.04 Обеспечение информационной безопасности телекоммуникационных систем и рабочей программой ЕН.01 Математика.
уметь:
выполнять операции над матрицами и решать системы линейных уравнений;
выполнять операции над множествами;
применять методы дифференциального и интегрального исчисления;
использовать основные положения теории вероятностей и математической статистики;
применять стандартные методы и модели к решению типовых вероятностных и статистических задач;
пользоваться пакетами прикладных программ для решения вероятностных и статистических задач;
планировать свое профессиональное развитее
информационные технологии для поиска и решения профессионально значимых задач
знать:
основы линейной алгебры и аналитической геометрии;
-основные положения теории множеств;
-основные понятия и методы дифференциального и интегрального исчисления;
-основные понятия и методы теории вероятностей и математической статистики;
-основные статистические пакеты прикладных программ;
-логические операции, законы и функции алгебры, логики
методы самоконтроля в решении профессиональных задач
способы и методы сбора, анализа и систематизации данных посредством информационных технологий
3 Структура дифференцированный зачёт:
3.1 Дифференцированный зачёт состоит из обязательной части, которая содержит по 3 вопроса.
3.2 Задания (вопросы) дифференцированного зачёта предлагаются в традиционной форме.
4 Система оценивания дифференцированного зачёта:
4.1 Каждый вопрос оценивается в 2 балла. За правильный ответ присуждается 2 балла. За неправильный ответ или его отсутствие ставиться 0 баллов. Оценка получается простым сложением баллов. Округление производить по правилам математики.
Критерии оценки:
оценка «5» - 6 баллов
оценка «4» - 4 балла
оценка «3» - 2 балла
6.2 Итоговая оценка за зачёт определяется как средний балл по всем вопросам.
6.3 Уровень владения материалом должен быть оценен не ниже чем на 2 балла.
5 . Время проведения зачёта
На подготовку к устному ответу на дифференцированном зачёте студенту отводится не более 20минут. Время устного ответа студента на дифференцированном зачёте составляет 10 минут.
Вопросы дифференциального зачёта:
Определение матрицы. Типы матриц
Действия с матрицами
Определители квадратной матрицы.
Алгебраическое дополнение и минор
Решение СЛУ методом обратной матрицы
Решение СЛУ методом Крамера
Решение СЛУ методом Гаусса
Каноническое уравнение прямой
Параметрическое уравнение прямой
Уравнение окружности
Предел переменной величины
Основные свойства пределов
Предел функции в точке и на бесконечности.
Понятие о непрерывности функции
Замечательные пределы
Правило Лапиталя
Определение производной
Частное значение производной
Правила и формулы дифференцирования
Производная сложной функции
Производная, геометрический и физический смысл.
Производная высших порядков.
Возрастание и убывание функции
Исследование функции на экстремум с помощью первой и второй производной
Выпуклость и вогнутость. Точки перегиба.
Применение производной к исследованию функции (по алгоритму).
Первообразная . Неопределенный интеграл. Основные свойства неопределенного интеграла
Методы интегрирования.
Определенный интеграл. Свойства определенного интеграла
Геометрический смысл определенного интеграла.
Методы вычисления определенных интегралов
Приложение определенного интеграла к решению прикладных задач.
Понятие ряда
Знакоположительные ряды. Признаки сходимости знакоположительных рядов
Знакопеременные ряды. Признаки сходимости знакопеременного ряда.
Дифференциальные уравнения.
Однородные дифференциальные уравнения
Неоднородные дифференциальные уравнения
Дифференциальные уравнения первого порядка
Дифференциальные уравнения высших порядков
Основные понятия комбинаторики
Основные понятия теории вероятности. Классическое определение вероятности
Законы сложения и умножения вероятностей
Случайные величины. Дискретные и непрерывные случайные величины.
Формула Бернулли
Числовые характеристики дискретной величины
Основные понятия и задачи математической статистики